Notion에서 작성한 글이라, 여기 에서 더 깔끔하게 보실 수 있습니다! 😮😊

---

[Beginner] Relative Ranks

[Relative Ranks]

Solution 1. Sort $O(n \lg n)$

def findRelativeRanks(self, score: List[int]) -> List[str]:
    score = sorted(enumerate(score), key=lambda x: -x[1])
    medals = {0:"Gold Medal", 1:"Silver Medal", 2:"Bronze Medal"}

    place = [0]*len(score)
    for i in range(len(score)):
        place[score[i][0]] = medals[i] if i in medals else str(i+1)

    return place

• enumerate를 이용하여 인덱스를 마킹해 놓고 점수를 기준으로 정렬시켜서 각 점수가 누구의 점수이며 그 점수를 받은 사람은 몇 등인지의 정보를 만들어 낸다.
• $n$만큼의 place 리스트를 만들어 놓고, score를 순회하며(첫 번째 원소가 1등, …, 끝에 있는 원소가 꼴등) 마킹해놓았던 인덱스를 이용해 place를 채워나간다.
  • 이 때, 등수 정보는 0-indexed임에 주의해야 한다.
• (등수):(메달) 형태의 key-value를 갖는 dictionary를 만들어 금/은/동메달을 각각 $O(n)$으로 탐색해서 치환해주는 것이 아닌 해시를 이용하여 Amortized $O(1)$에 치환해준다.

Solution 2. Heap $O(2n \lg n)$

def findRelativeRanks(self, score: List[int]) -> List[str]:
    n = len(score)
    heap = []
    place = [0]*n
    medals = {0:"Gold Medal", 1:"Silver Medal", 2:"Bronze Medal"}

    for i in range(n):
        heappush(heap, (-score[i], i))
    
    for i in range(n):
        place[heappop(heap)[1]] = medals[i] if i in medals else str(i+1)
    
    return place

• 전체적인 흐름은 Solution 1.과 비슷하다. 점수의 최댓값을 보고 차례대로 순위를 매겨줄 것이므로, 최대 힙을 이용하기 위해 -를 붙여서 기존 인덱스 정보와 함께 heappush()한다. 이렇게 최대 힙을 구성하고 나면, heappop()을 이용하여 1등부터 차례대로 인덱스를 빼내어 순위 정보를 갱신해 주는 식이다.

Solution 2-2. Heap $O(n \lg n)$

def findRelativeRanks(self, score: List[int]) -> List[str]:
    n = len(score)
    place = [0]*n
    medals = {0:"Gold Medal", 1:"Silver Medal", 2:"Bronze Medal"}

    heap = [(-s, i) for i, s in enumerate(score)]
    heapify(heap)
    
    for i in range(n):
        place[heappop(heap)[1]] = medals[i] if i in medals else str(i+1)
    
    return place

• Solution 2.에서는 인덱스 정보를 붙여서 최대 힙을 구성하는 데에 $O(n \lg n)$ 시간을 소모했다. 여기에서 시간복잡도를 줄이기 위해 주목할 점은, 원소 하나씩 heappush() 하여 힙을 구성하는 방식과, heapify()로 한 번에 힙을 구성하는 시간에는 차이가 있다.
  • heapify()는 $O(n)$에 리스트를 힙으로 만들어 준다. 이를 이용하기 위해, 먼저 enumerate를 이용하여 $O(n)$에 점수와 인덱스를 묶어 놓고, heapify()를 이용하여 $O(n)$에 최대 힙을 구성한다.

---

[Middler] 더 맵게

[더 맵게]

Solution 1. Heap $O(3n \lg n)$

from heapq import *

def solution(scoville, K):
    heapify(scoville)
    cnt = 0
    
    while scoville[0] < K and len(scoville) >= 2:
        heappush(scoville, heappop(scoville)+heappop(scoville)*2)
        cnt += 1
        
    if scoville[0] < K: return -1
    else: return cnt

• 반복적으로 최솟값을 이용하여 섞는다는 점에 주목하면 삽입에 $O(\lg n)$, 삭제에 $O(\lg n)$이 소요되는 Priority Queue를 생각할 수 있다.
• heap의 또다른 장점은, 그 특징 때문에 최솟값을 $O(1)$에 확인할 수 있다는 것이다. (항상 반정렬 상태를 유지하며, 맨 앞 원소가 최솟값)
• 모든 음식의 스코빌 지수를 $K$ 이상으로 만든다 ⇒ 스코빌 지수의 최솟값이 $K$ 이상이다 임을 관찰하면 쉽게 풀린다.

Solution 2. Heap + Queue $O(2n \lg n)$

from heapq import *
from collections import deque

def mix(f, h, q):
    if h[0] < q[0]: q.append(f + 2*heappop(h))
    else: q.append(f + 2*q.popleft())

def solution(scoville, K):
    heapify(scoville)
    queue = deque([])
    cnt = 0

    while len(scoville)+len(queue) > 1:
        if min(scoville[0] if scoville else queue[0], queue[0] if queue else scoville[0]) >= K:
            return cnt
        
        if scoville and queue:
            if scoville[0] < queue[0]:
                first = heappop(scoville)
                if scoville: mix(first, scoville, queue)
                else: queue.append(first + 2*queue.popleft())
            else:
                first = queue.popleft()
                if queue: mix(first, scoville, queue)
                else: queue.append(first + 2*heappop(scoville))
        
        elif scoville:
            queue.append(heappop(scoville) + 2*heappop(scoville))
        
        else:
            queue.append(queue.popleft() + 2*queue.popleft())

        cnt += 1

    if min(scoville[0] if scoville else queue[0], queue[0] if queue else scoville[0]) >= K:
        return cnt
    else: return -1

• 많은 조건 분기를 통해 실행속도를 개선시켰다.
• 주요 특징은, heappush()하는 데에 걸리던 $O(\lg n)$ 대신 queue에 append()함으로써 Amortized $O(1)$로 줄였다.
• 또한 특정한 경우(섞였던 값(queue[0])이 한 번도 섞이지 않은 최소 스코빌 지수(scoville[0])보다 작을 때), 기존에 heappop 하는 데에 걸리던 $O(\lg n)$ 대신 queue에서 popleft()함으로써 $O(1)$로 줄였다.
• 시간복잡도를 생각해 보자. 최악의 경우는 popleft()로 시간복잡도상의 이득을 못 보는 경우라고 볼 수 있다. 다만 이 경우에도 heappush() 대신 append() 을 이용함으로써 $O(\lg n)$ 대신 Amortized $O(1)$로 줄어든다. ∴ $O(2n \lg n)$
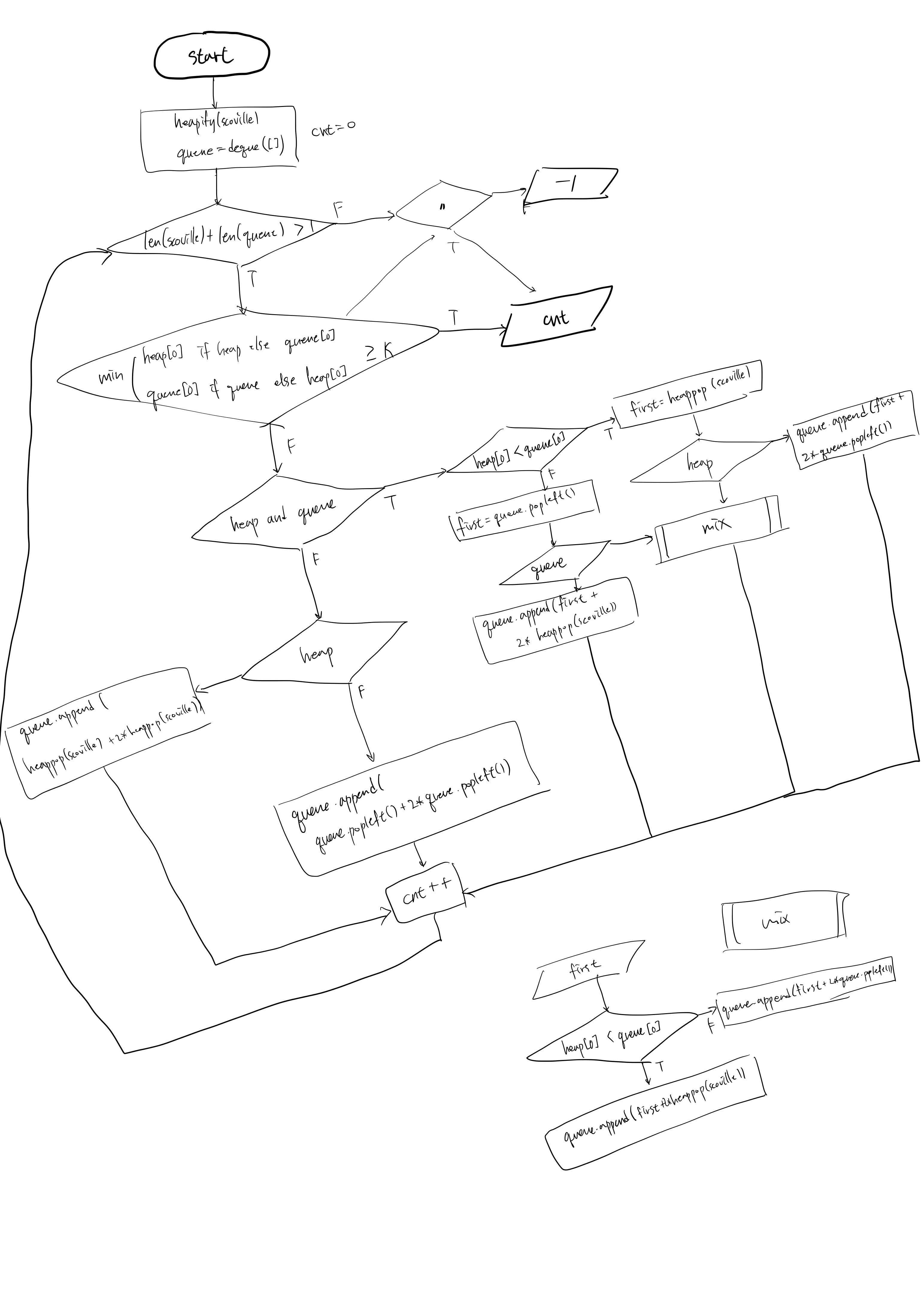
  (처절한 조건 분기의 흔적,,,)

Solution 3. Queue $O(n \lg n)$

def solution(scoville, K):
    scv = deque(sorted(scoville))
    mixed = deque()
    cnt = 0

    while (scv and scv[0]<K) or (mixed and mixed[0]<K):
        if len(scv)+len(mixed) < 2:
            return -1

        item = [0]*2
        for i in range(2):
            if scv and mixed:
                if scv[0] < mixed[0]:
                    item[i] = scv.popleft()
                else:
                    item[i] = mixed.popleft()
            elif scv:
                item[i] = scv.popleft()
            else:
                item[i] = mixed.popleft()
        
        mixed.append(item[0] + 2*item[1])
        cnt += 1
    
    return cnt

• 더 빠르게 동작시킬 방법이 없을지 다른 분들의 코드를 찾아보다가, 아마 가장 빠른 코드를 발견했다. 이 링크 가 이 코드의 원본이다.
• Solution 2.의 다소 지저분했던 casework를 반복문을 이용하여 아주 아름답게 해결하셨다. 반복되는 조건을 이용하여 계속해서 조건 분기를 해나가야하는 상황에서는 반복문을 꼭 고려해보아야 겠다. 조건 분기의 depth가 깊어질 수록 이 방법이 매우 아름다워진다.
• 처음부터 scoville을 정렬시켜서 queue로 바꾼다. 이를 통해 얻는 효과는, Solution 2.에서처럼 heappop() 을 통해 매번 $O(\lg n)$으로 heap을 유지시켜서 최솟값을 $O(1)$에 찾을 수 있도록 할 필요가 없다.
  • 미리 완전히 정렬시켜 놓고 popleft() 만 한다면, 정렬된 상태가 유지되기때문에 여전히 최솟값을 $O(1)$에 찾을 수 있게 된다.

---

[Challenger] 최소 힙

[최소 힙]

• Priority Queue의 기본 문제 격인 이 문제가 챌린저 문제로 나왔다는 것은 아마 직접 구현해보라는 뜻일 것 같다. 밥 먹고 구현해봐야지 ㅎㅎ

Solution 1. $O(n \lg n)$

from heapq import *

heap = []

for _ in range(int(input())):
    n = int(input())
    if n: heappush(heap, n)
    else: print(heappop(heap) if heap else 0)

---