행렬이란?(알면 Keep)
행렬 개요
출처인 수학방으로 가시면 더 자세한 설명이 있습니다!
행렬 곱셈 순서 문제를 설명드리기 전에, 행렬이 익숙하지 않은 분들을 위해 행렬부터 설명드리려 합니다.
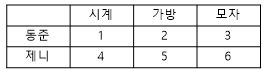
동준이와 제니가 가지고 있는 시계, 가방, 모자의 수를 표로 나타냈습니다.
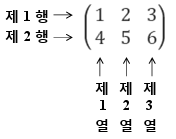
숫자나 문자를 직사각형 모양으로 배열한 후 양쪽을 괄호로 나타낸 것이 행렬(Matrix)입니다. 가로 배열을 행(row)라고 하고, 세로 배열을 열(column)이라고 합니다.
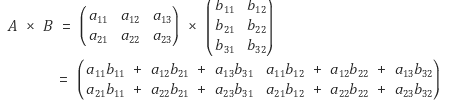
행렬에서의 곱은 행렬간의 더하기, 빼기와는 다르게 (x 기호 앞의 행렬의 열의 개수) = (x 뒤에 있는 행렬의 행의 개수)일때만 곱셈이 가능합니다.
- 그 이유는 행렬이 일차변환을 연구하는 데서 나타났기 때문인데, 일차변환의 합성과 관련한 성질 때문입니다.
- 행렬간의 나눗셈은 정의되지 않습니다.
(더 알아보기)
행렬과 일반적인 수들이나 다항식과 성질의 차이가 있습니다.
알고리즘 문제 풀이
한국외대 신찬수 교수님의 알고리즘 강의를 정리한 내용입니다. 유튜브로 볼 수 있으니 자세한 내용은 출처로 이동하시면 됩니다. 출처 이동하기
행렬곱의 시간 복잡도
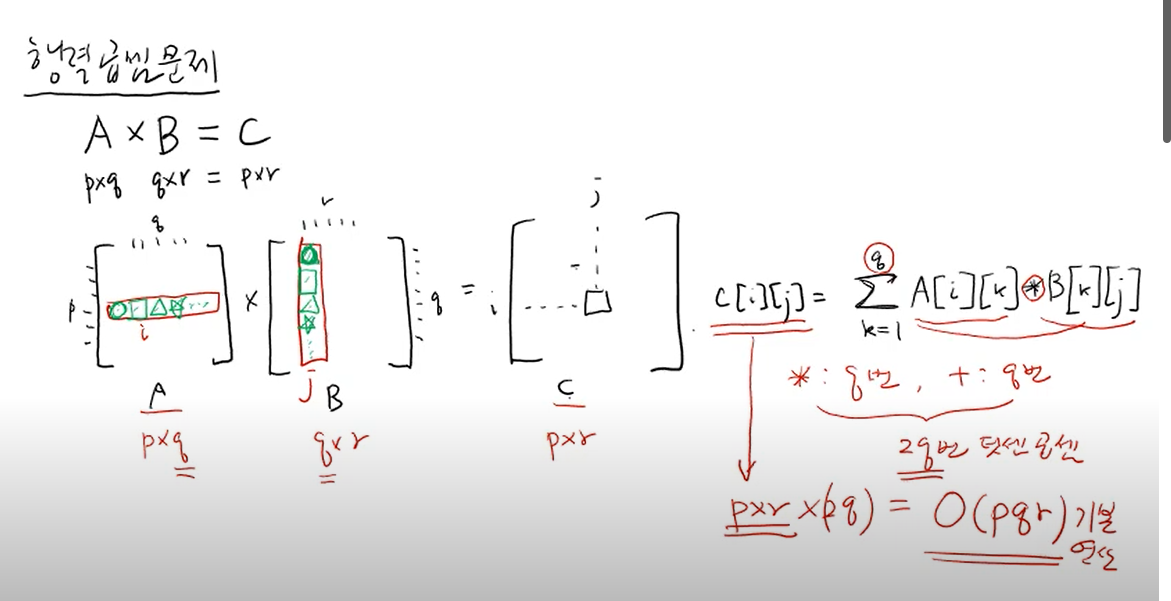
행렬 곱셈 문제에서는 시간 복잡도가 O(pqr)입니다.
그 이유는 행렬곱의 결과인 C 행렬이 p x r의 크기이고, C의 성분(entry)인 C[i][j]가 행렬 A의 p행과 행렬 B의 r열의 곱(*)으로 q번만큼 더해지기(+) 때문에
p x r x (2q) = O(pqr)
이 기본적인 연산 횟수가 됩니다.
행렬 곱셈 순서 문제
그렇다면 행렬 곱셈의 순서는 왜 문제가 됐을까요?
그 이유는 행렬곱은 교환법칙이 성립하지 않기 때문에 연산 순서(결합의 순서)에 따라 기본 연산의 횟수(pqr)가 달라지기 때문입니다.

예를들어 위의 M1 x M2 x M3의 행렬 곱셈 문제에서도
((M1 x M2) x M3)로 계산한 연산 횟수는 32번
(M1 x (M2 x M3))로 계산한 연산 횟수는 60번
이 되는 것입니다.
위의 경우 ((M1 x M2) x M3)로 괄호를 치는 것이 유리하겠죠?
그러나, 행렬이 4개로 늘어나면 괄호치는 경우의 수는 5개, 5개일 땐 14개, 6개일 땐 42개 ...로 기하급수적으로 늘어납니다. (이를 catalan 수라고 부릅니다.)
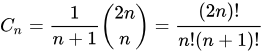
그렇다면 그러한 경우의 수 중 연산 횟수가 최소가 되는 경우를 찾는 것이 연산 성능을 높일 수 있겠네요!(나아가 시스템의 성능도 높일 수 있는 개발자가 되겠죠?)
11049 행렬 곱셈 순서
연산 횟수가 최소가 되는 경우를 구하는 알고리즘은 동적 프로그래밍 알고리즘을 활용합니다.
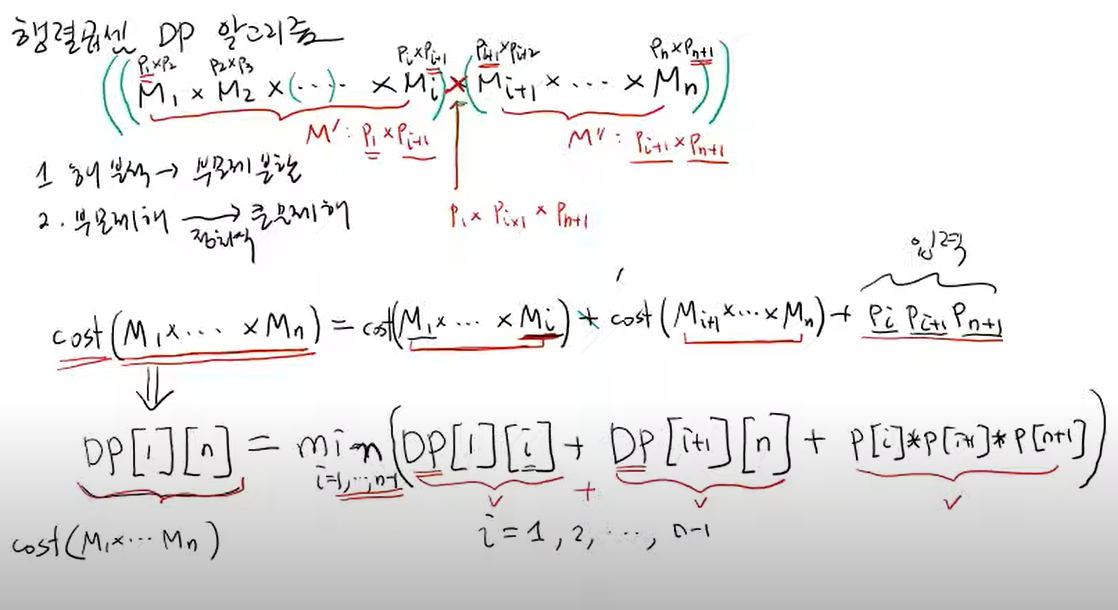
그 이유는 행렬의 연산 횟수는 (( M1 x M2 x ... x Mi) x (Mi+1 x ... Mn)) 처럼 어디에 괄호를 치느냐, 다시 말해 어떻게 나누느냐의 문제이기 때문입니다.
위 처럼 전체 문제의 해를 분석했더니 부분 문제로 분할할 수 있겠네요. 그렇다면 부분 문제를 더 잘게 쪼개서 규칙을 찾아 점화식을 만들어 큰 문제(전체 문제)의 해를 구할 수 있겠네요! 전형적인 DP 문제입니다.
정리하자면, 큰 문제를 계속 쪼개서 부분 문제들의 최소를 구하여 모두 더하면 전체 문제 또한 최소가 된다는 말이 됩니다.
즉, cost(M1 x M2 x ... Mn) = cost(M1 x ... Mi) + cost(Mi+1 x ... x mn) + Pi x Pi+1 x Pn+1 의 값을 구하면 됩니다.
여기서 Pi x Pi+1 x Pn+1은 저 두 덩어리의 행렬곱의 결과인 i번째 매트릭스는 i행 x i+1열로 이루어져 있고, n번째 매트릭스는 i+1행 x n+1열로 이루어져 있기 때문입니다.(i는 1도 될 수 있어요.)
but! 저 중요한 i를 모르기 때문에 모두 탐색해보아야 합니다.(i = 1부터 n까지 모두다요!)
그래서 DP라는 2차원 리스트에 연산 횟수를 담아 최종 연산 횟수가 최소가 되는 경우를 찾을겁니다.
위 식의 점화식을 코드로 구현하면
DP[1][n] = min(DP[1][i] + DP[i+1][n] + P[i]*P[i+1]*P[n+1])
# DP[1][n] = cost(M1 x ... x Mn)
# min의 range는 i = 1, ... , n-1-
문제 개요
크기가 N×M인 행렬 A와 M×K인 B를 곱할 때 필요한 곱셈 연산의 수는 총 N×M×K번이다. 행렬 N개를 곱하는데 필요한 곱셈 연산의 수는 행렬을 곱하는 순서에 따라 달라지게 된다.
예를 들어, A의 크기가 5×3이고, B의 크기가 3×2, C의 크기가 2×6인 경우에 행렬의 곱 ABC를 구하는 경우를 생각해보자.
AB를 먼저 곱하고 C를 곱하는 경우 (AB)C에 필요한 곱셈 연산의 수는 5×3×2 + 5×2×6 = 30 + 60 = 90번이다.
BC를 먼저 곱하고 A를 곱하는 경우 A(BC)에 필요한 곱셈 연산의 수는 3×2×6 + 5×3×6 = 36 + 90 = 126번이다.
같은 곱셈이지만, 곱셈을 하는 순서에 따라서 곱셈 연산의 수가 달라진다.
행렬 N개의 크기가 주어졌을 때, 모든 행렬을 곱하는데 필요한 곱셈 연산 횟수의 최솟값을 구하는 프로그램을 작성하시오. 입력으로 주어진 행렬의 순서를 바꾸면 안 된다. -
입력
3
5 3
3 2
2 6 -
출력
90

