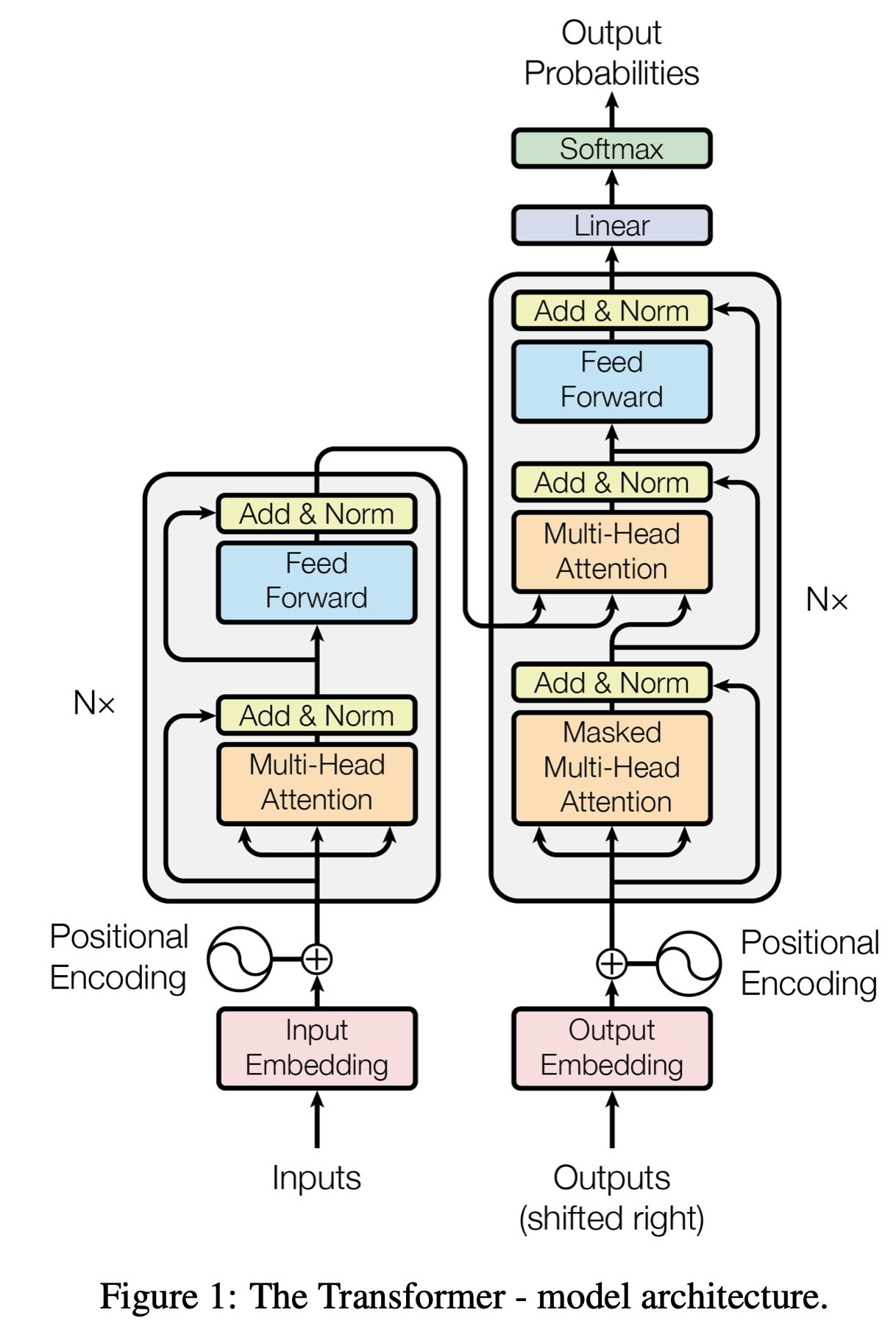
지금까지 위 Transformer Decoder에 위치하는 대부분의 component들에 대해 알아보았다.
순서대로 나열해보면
- Token Embedding
- Positional Embedding
- Self-Attention
- Masked Multi-Head Attention
이렇게 알아봤는데, 구조에서 가장 위쪽에 Feed Forward가 존재하는 것을 확인할 수 있다.
class FeedForward(nn.Module):
"""a simple linear layer followed by a non-linearity """
def __init__(self, n_embd):
super().__init__()
self.net = nn.Sequential(
nn.Linear(n_embd, 4 * n_embd),
nn.ReLU(),
nn.Linear(4 * n_embd, n_embd), # proj
)
def forward(self, x):
return self.net(x)위와 같이 FeedForward network를 만든다.
이 모듈은 self-attention module바로 뒤에 위치하게 된다.
여기서 Linear는 per token level로 모든 token에 독립적으로 적용되는데, self-attention에서 모든 sequence에 대해서 communication을 진행을 했으니, Linear 에서는 개별 token에서 진행.
최종적으로 Block이 xN 번 구성되는 것으로 아키텍처가 이뤄져 있는데, 여기서 한가지 optimization을 도와주는 두가지 방법이 들어가는데 하나가 Residual connection , 다른 하나는 Layer Normalization이다.
Residual Connection
input -> target 에서 block이 배우는 것은 오직 plus되는 부분만 학습을 하면 되는 것임.
backpropagation할 때, 효과적임(나중에 다른 포스트에서 언급하겠음)
LayeNorm
BatchNorm이랑 비슷한데, BatchNorm은 Batch dimension에서 정규화가 일어나는 것
module = BatchNorm1d(100)
x = torch.randn(32, 100) # batch size 32 of 100-dimensional vectors
x = module(x)
x.shapetorch.Size([32, 100])x[:, 0].mean(), x[:, 0].std() # mean, std of one feature across all batch inputs(tensor(7.4506e-09), tensor(1.0000))x[0, :].mean(), x[0, :].std() # mean, std of a single input from the batch, of its features(tensor(0.0411), tensor(1.0431))이런식으로 0 mean에 1 std 를 가지게 된다. (feature 별로)
LayerNorm은 row단위로 진행을 하는데
x[:, 0].mean(), x[:, 0].std() # mean, std of one feature across all batch inputs(tensor(0.1469), tensor(0.8803))x[0, :].mean(), x[0, :].std() # mean, std of a single input from the batch, of its features(tensor(-9.5367e-09), tensor(1.0000))이렇게 진행된다. (sequence 단위로 된다는 의미)
buffer도 필요 없게 된다. (BN에서는 inference시에 buffer가 필요, 필요없음)
class Block(nn.Module):
""" Transformer block : communication followed by computation """
def __init__(self, n_embd, n_head):
# n_embd: embedding dimension, n_head: the number of heads we'd like
super().__init__()
head_size = n_embd // n_head
self.sa = MultiHeadAttention(n_head, head_size)
self.ffwd = FeedForward(n_embd)
self.ln1 = nn.LayerNorm(n_embd)
self.ln2 = nn.LayerNorm(n_embd)
def forward(self, x):
x = x + self.sa(self.ln1(x))
x = x + self.ffwd(self.ln2(x))
return xclass BigramLanguageModel(nn.Module):
def __init__(self):
super().__init__()
# each token directly reads off the logits for the next token from a lookup table
self.token_embedding_table = nn.Embedding(vocab_size, n_embd)
self.position_embedding_table = nn.Embedding(block_size, n_embd)
self.blocks = nn.Sequential(*[Block(n_embd, n_head=n_head) for _ in range(n_layer)])
self.ln_f = nn.LayerNorm(n_embd)
self.lm_head = nn.Linear(n_embd, vocab_size)
def forward(self, idx, targets=None):
B, T = idx.shape
# idx and targets are both (B,T) tensor of intergers
tok_emb = self.token_embedding_table(idx) # (B,T,C)
pos_emb = self.positional_embedding_table(torch.arange(T, device=device)) # (T,C)
x = tok_emb + pos_emb # (B, T, C)
x = self.blocks(x) # (B, T, C)
x = self.ln_f(x) # (B, T, C)
logits = self.lm_head(x) # (B, T, vocab_size)
if targets in None:
loss = None
else:
B, T, C = logits.shape
logits = logits.view(B*T, C)
targets = targets.view(B*T)
loss = F.cross_entropy(logits, targets)
return logits, loss
def generate(self, idx, max_new_tokens):
# idx is (B, T) array of indices in the current context
for _ in range(max_new_tokens):
# crop idx to the last block_size tokens
idx_cond = idx[:, -block_size:]
# get the predictions
logits, loss = self(idx_cond)
# focus only on the last time step
logits = logits[:, -1, :] # becomes (B, C)
# apply softmax to get probabilities
probs = F.softmax(logits, dim=-1) # (B, C)
# sample from the distribution
idx_nex = torch.multinomial(probs, num_samples=1) # (B, 1)
# append sampled index to the running sequence
idx = torch.cat((idx, idx_next), dim=1) # (B, T+1)
return idx