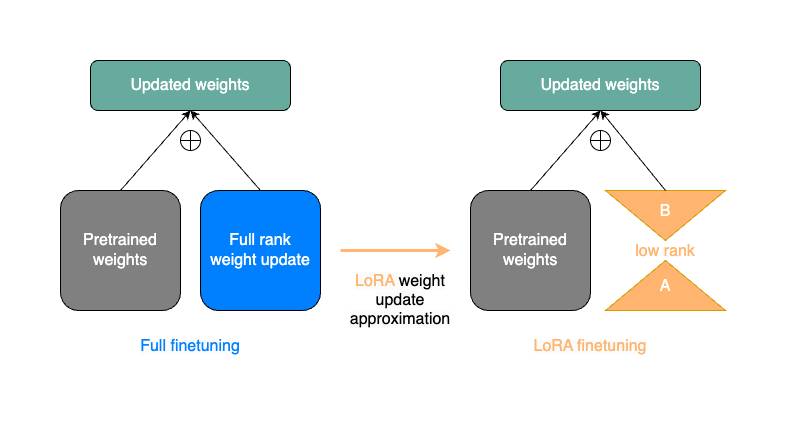
Reference : https://pytorch.org/torchtune/stable/tutorials/lora_finetune.html
How LoRA works
- LoRA의 기본적인 아이디어는 pre-trained matrices (i.e. paprameters of the original model)을 frozen한 상태로 작은 small delta를 original matrix에 더해줌으로써 original matrix보다 적은 parameter를 학습하는데 의미를 가짐.
- Updated weight matrices를 구하기 위해, 와 동일한 사이즈이면서 low rank를 지니는 작은 parameter들을 학습함으로써, weight를 업데이트 하는 방법 (?)
- 무슨 말인지는 알겠는데 저는 LLM에서 weight matrix가 가지는 의미에 대해서 이해가 안갈 수 있음.
- 내가 이해한 바는
-> LoRA는 pre-trained된 matrix를 효율적으로 fine-tuning하는 방법론으로, full fine-tuning이 아니라, low-rank의 delta weight를 학습함으로써 그 delta weight (결국 full fine-tuning했을 때 원래 pretrained에서 업데이트 되었어야할)를 학습을 통해 찾아내서 기존 frozen matrix + delta weight를 더하는 방법으로 이해.
- LoRA 같은 경우 추가적인 parameter들이 forward에서 발생하지만,
AandBmatrices만 학습을 진행함. - 이는 원래 저장을 위해 필요했던 gradient의 수를
in_dim*out_dim에서r*(in_dim+out_dim)으로 획기적으로 줄여줌 (r은 매우 작음in_dim이랑out_dim이랑 비교했을 때는) - LLaMA2의 self-attention Q,K, V projection에 필요한 dimension은
in_dim=out_dim=4096. r=8로 decomposition하면 4096*4096=15M→8*8192=65K.
실제 코드단에서는 다음과 같이 적용됨.
from torch import nn, Tensor
class LoRALinear(nn.Module):
def __init__(
self,
in_dim: int,
out_dim: int,
rank: int,
alpha: float,
dropout: float
):
# These are the weights from the original pretrained model
self.linear = nn.Linear(in_dim, out_dim, bias=False)
# These are the new LoRA params. In general rank << in_dim, out_dim
self.lora_a = nn.Linear(in_dim, rank, bias=False)
self.lora_b = nn.Linear(rank, out_dim, bias=False)
# Rank and alpha are commonly-tuned hyperparameters
self.rank = rank
self.alpha = alpha
# Most implementations also include some dropout
self.dropout = nn.Dropout(p=dropout)
# The original params are frozen, and only LoRA params are trainable.
self.linear.weight.requires_grad = False
self.lora_a.weight.requires_grad = True
self.lora_b.weight.requires_grad = True
def forward(self, x: Tensor) -> Tensor:
# This would be the output of the original model
frozen_out = self.linear(x)
# lora_a projects inputs down to the much smaller self.rank,
# then lora_b projects back up to the output dimension
lora_out = self.lora_b(self.lora_a(self.dropout(x)))
# Finally, scale by the alpha parameter (normalized by rank)
# and add to the original model's outputs
return frozen_out + (self.alpha / self.rank) * lora_out# Print the first layer's self-attention in the usual Llama2 model
>>> print(base_model.layers[0].attn)
CausalSelfAttention(
(q_proj): Linear(in_features=4096, out_features=4096, bias=False)
(k_proj): Linear(in_features=4096, out_features=4096, bias=False)
(v_proj): Linear(in_features=4096, out_features=4096, bias=False)
(output_proj): Linear(in_features=4096, out_features=4096, bias=False)
(pos_embeddings): RotaryPositionalEmbeddings()
)
# Print the same for Llama2 with LoRA weights
>>> print(lora_model.layers[0].attn)
CausalSelfAttention(
(q_proj): LoRALinear(
(dropout): Dropout(p=0.0, inplace=False)
(lora_a): Linear(in_features=4096, out_features=8, bias=False)
(lora_b): Linear(in_features=8, out_features=4096, bias=False)
)
(k_proj): Linear(in_features=4096, out_features=4096, bias=False)
(v_proj): LoRALinear(
(dropout): Dropout(p=0.0, inplace=False)
(lora_a): Linear(in_features=4096, out_features=8, bias=False)
(lora_b): Linear(in_features=8, out_features=4096, bias=False)
)
(output_proj): Linear(in_features=4096, out_features=4096, bias=False)
(pos_embeddings): RotaryPositionalEmbeddings()
)위에서 볼 수 있듯이, 기존의 matrix에 해당하는 4096 * 4096의 pretrained weight를 고정하고, 학습가능한 low-rank linear A, B matrix를 사용하여 이들을 학습함으로써 weight를 업데이트(?)할 수 있는 를 찾아냄.