GOAL : Uncertainty quantification in large language models (LLMs)
위 논문에서는 LLMs에서의 불확실성 측정을 다룬 논문.
Contributions
- Decouple Epistemic and aleatoric uncertainty
- Aim to identify when only the epistemic uncertainty is large
이게 무슨말인가 ?
-
Epistemic uncertainty : Ground truth에 대한 knowledge의 부족 (데이터 부족) - 학습을 통해 해결 가능
-
Aleatoric uncertainty : 예측 문제의 무작위성으로 인한 줄일 수 없는 불확실성 - 학습으로 해결 불가능
- Same query에 대한 여러개의 정답을 가진 경우
- For example : What is the capital of the UK ? 이 쿼리의 경우 aleatoric uncertainty가 높지 않음. (single label query)
- Name a city in the UK : 이 쿼리의 경우 aleatoric uncertainty가 있음. (multi-label queries)
-
위 관점에서 truthfulness는 epistemic uncertainty로 볼 수 있음.
- epistemic uncertainty가 낮다는 의미는 곧 ground truth에 가깝다는 의미. (no hallucination)
-
이전 연구(estimating entropy, ensembling, conformal prediction)에서의 공통적인 한계점
- 오직 하나의 올바른 응답만이 정답인 문제 상황을 가정하는 경우가 많음. (즉, aleatoric uncertainty가 거의 없는 경우)
- 만약 여러 응답이 올바른 경우는 어떨까 ?
- 정답에 aleatoric uncertainty가 존재하게 됨.
- 기존의 방법은 이를 고려하지 않음
결국 하고 싶은 것은 ?
- Multi-response queries를 효과적으로 다룰 수 있도록 epistemic uncertainty가 높은 상황을 탐지하고 배제하자.
High epistemic uncertainty를 어떻게 측정할 수 있을까 ?
- 프롬프트에서 가능한 응답을 여러 번 반복하면, 언어 모델의 출력에 뚜렷한 영향을 미칠 수 있음
- 이를 이용해서 epistemic uncertainty is high vs aleatoric uncertainty is high 를 구분
예시 )

- 여기서 sentence 를 반복한다.
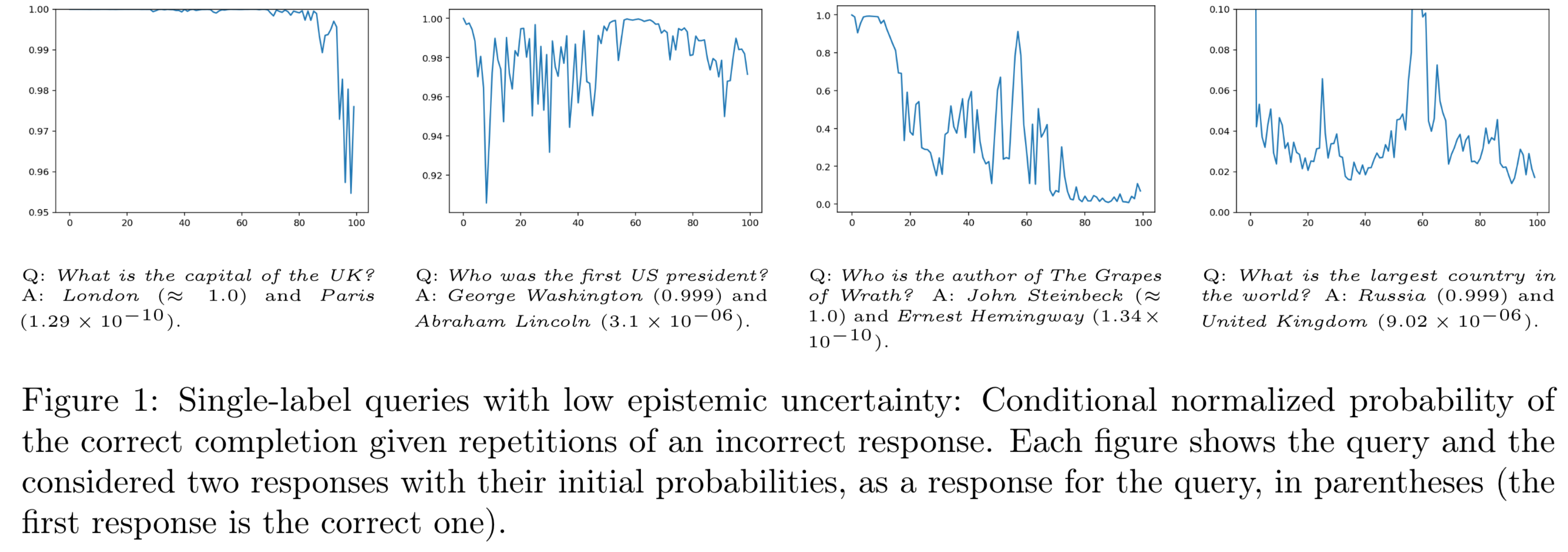
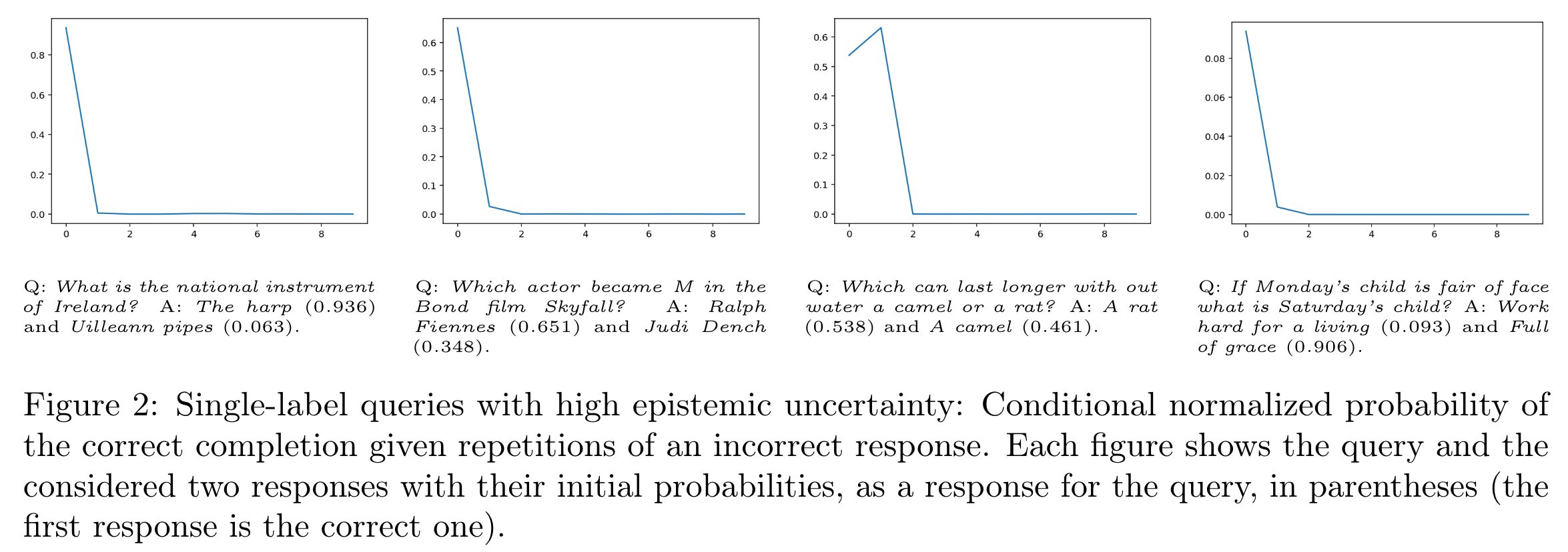
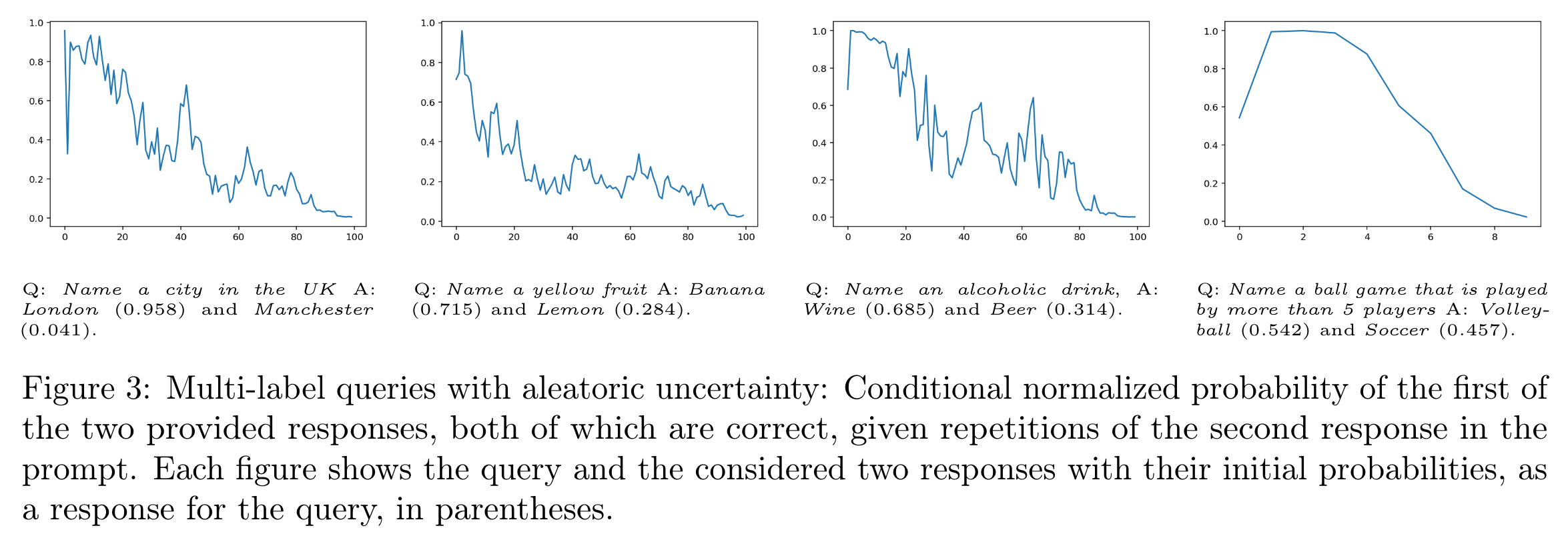
- Figure 1같은 경우 correct response : 이고, 이에 대한 반복으로 를 100번까지 반복하지만, 96%까지밖에 떨어지지 않음.
- 반면에 Figure 2에서, 라는 질문의 답으로 와 가 높은 확률로 나왔고, 이번엔 incorrect response를 여러번 입력했을 때, probability가 심하게 떨어지는 모습을 볼 수 있음.
- 마지막으로, multi-label queries가 correct answer인 경우 상대적으로 Figure 2에 비해서 크게 유지되는 것을 확인할 수 있음.
결국 어떻게 Epistemic uncertainty를 측정하는가 ?
notation
: the space of finite text sequences
: be the ground-truth conditional probability distribution over text sequences given a prompt
: be the learned language model.
Assumption 4.1 (Ground truth independence assumption). The ground-truth satisfies
for any and any .
위 assumption은 이전의 샘플에 의한 query가 영향을 주지 않는 것을 가정함.
예를들어 를 입력했을 때, 의 확률이 만약에 이 들어온다고 해서, 달라지지 않음을 의미.
Definition 4.2 (Pseudo joint distribution). Given a family of prompt functions , a conditional distribution , and , we use notation to denote a pseudo joint distribution defined as
예를들어, 를 입력으로 나올 확률, 나올 확률 이런거 다 Assumption 4.1에 의해 joint distribution으로 표현 가능.
Remark 4.3 (Sampling from ). Note that sampling from can be simply done through a chain-rule-like procedure as can be seen from the above definition, that is to have we draw , , , and so on.
-
To measure epistemic uncertainty, we need to quantify how far the estimated pseudo joint distribution is from the ground truth . One natural choice is the following definition:
예를 들어, , …
이 들어왔을 때, 를 로 샘플링 가능,
를 가지고 pseudo joint distribution 를 구해야 epistemic uncertainty를 구할 수 있음.
Definition 4.4 (Epistemic uncertainty metric). Given an input , we say that the epistemic uncertainty of is quantified by .
따라서, Epistemic uncertainty를 다음과 같이 구할 수 있다.
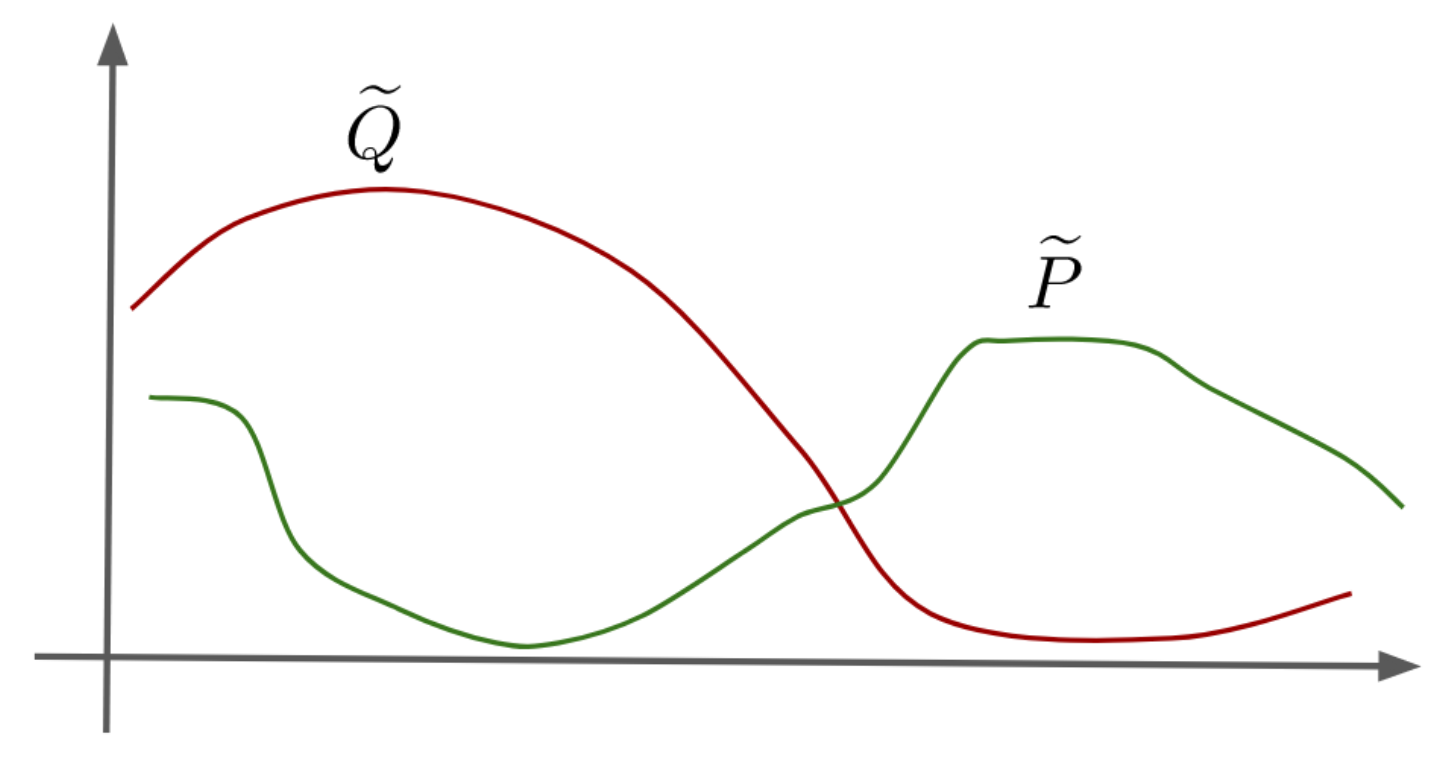
따라서, 은 얼마나 가 에 잘 근사하는지를 측정한다.
- 이 메트릭은 가 작은 확률을 가지는 사건에 가 큰 확률을 할당하는지 확인가능.
- LLM에서 이는 모델이 언어의 일반적인 사용에서 가능성이 낮은 시퀀스를 생성한다는 것을 의미.
- 위 그림에서 가 실제 정답으로 도출된 분포, 는 hallucination을 겪는 상황을 나타냄.
- 입력 가 주어졌을 때, 위 hallucination metric()을 추정하고 싶은데, 우리는 실제로 에만 접근이 가능하기 떄문에 명시적으로 계산하는 것은 불가능
- 하지만, 가정 4.1하에서 를 에만 의존하는 값으로 하한을 설정할 수 있음 (증명은 Appendix)
Theorem 4.5. For all pseudo joint distributions satisfying Assumption 4.1, we have that
- 정리에서의 하한은 모든 에 대해 균일하게 적용, 이 때 에 기반해서 계산이 가능
- 여기서 는 실제 쿼리에 대한 확률 를 독립적이라고 가정한 확률 분포.
- 무슨 의미냐면 어떤 쿼리에 대한 응답 이 번 째 위치할 때 나올 확률을 결합확률로 나타낸 것.
- 예를들어서 “London”이 i 번째 위치할 때 나올 확률을 모두 곱한 것
- 위 정리는 mutual information을 통한 epistemic uncertainty의 하한을 제공함
- 그러나 이런 mutual information은 무한한 문자열에 대해 관찰해야 하기 때문에 불가능
- 를 유한한 분포로 대체, 아래 알고리즘 방식을 사용.

Score-based hallucination tests
- : 알고리즘 1에서 로 계산된 값으로, 쿼리 에 대한 explicit dependence를 강조.
- 불확실성 추정값 : 주어진 쿼리 에 대한 LLM의 hallucination 정도를 나타내는 점수로 사용
- 이 점수를 통해 응답을 포기(abstain)할지 결정 가능
예를 들어, "What is the capital of the UK?"라는 쿼리에 대해 시스템이 "London"과 "Manchester"라는 두 개의 응답을 제공했다고 가정, 알고리즘을 통해 계산된 불확실성 추정치가 0.8이라고 보면, 시스템은 점수가 0.5 이상이면 응답을 제공하지 않는다고 했을 때, 응답을 hallucination으로 간주, 제공x.
Abstention policy
- Hallucination으로 간주되는 경우 응답을 포기하는 시스템
- Score-based abstention methods: 사용자에 의해 선택된 점수 (예로 응답 가능성이나 등)에 따라 임계값 설정, 이 임계값 초과 시 hallucination으로 선언.
Experiments
Language model
- Gemini 1.0 Pro : output이랑 score생성
Datasets
- TriviaQA : 50,000개의 무작위로 선택된 데이터 사용. 주로 단일 레이블 쿼리를 포함
- AmbigQA 데이터셋: 전체 데이터셋(12,038개)을 사용. 이 데이터셋도 주로 단일 레이블 쿼리를 포함
- WordNet 기반 다중 레이블 데이터셋: 각 데이터는 (개체, 자식들) 형태로 구성되며, "개체의 유형을 말하시오." 라는 쿼리를 만들고 자식들을 목표 레이블로 간주.
- “Name a type of entity”
Baselines
- the probability of the greedy response (denoted by T 0);
- the semantic-entropy method(denoted by S.E.).
- Proposed mutual information score (denoted by M.I)
- Self-verification method (denoted by S.V.)
- 쿼리 에 대해 첫 번째로 가장 큰 확률을 가지는 을 찾음
- 이후 다음 쿼리에 대해 “True”, “False”토큰 확률 계산
- “Consider the following question : Q: . One answer to question is . Is the above answer to question correct ? Answer True or False. A :”.
Results
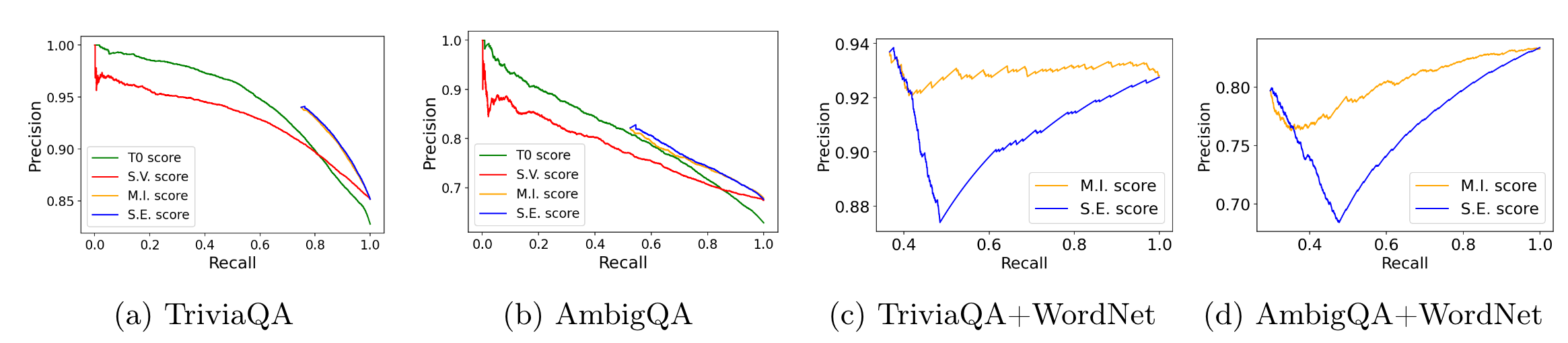
- Recall : 회피하지 않는 쿼리의 비율 (응답을 하는 쿼리의 비율)
- Precision : 회피하지 않은 쿼리 중 올바른 결정의 비율
그림에서 무슨의미냐 ?
-
S.E., M.I., 는 Recall이 매우 높은 지점에서 시작한다.
- TriviaQA와 AmbigQA는 대부분 단일 레이블 쿼리를 포함하기 때문에 시스템이 쿼리에 대한 응답을 회피할 필요성이 낮다. 즉 epistemic uncertainty가 낮은 데이터셋
-
M.I. 방법이, S.V. 기준선보다 더 우수하지만, S.E. 방법과 비슷한 성능.
-
AmbigQA 데이터셋은 일부 다중 레이블 쿼리를 토함하고 있지만, 대부분 쿼리에 대해 LLM이 낮은 엔트로피를 가지고 있음을 관찰.
-
이상적으로 LLM은 다중 레이블 쿼리에 대해 더 높은 엔트로피를 가져야 함.
-
이러한 쿼리를 사용하려고 TriviaQA와 AmbigQA를 WordNet과 합친 다중 레이블 쿼리 데이터셋을 구성
-
(c,d)에서 낮은 리콜값을 제외하고, S.E. 방법은 다중 레이블 데이터의 추가로 인해 성능이 눈에 띄게 저하됨.
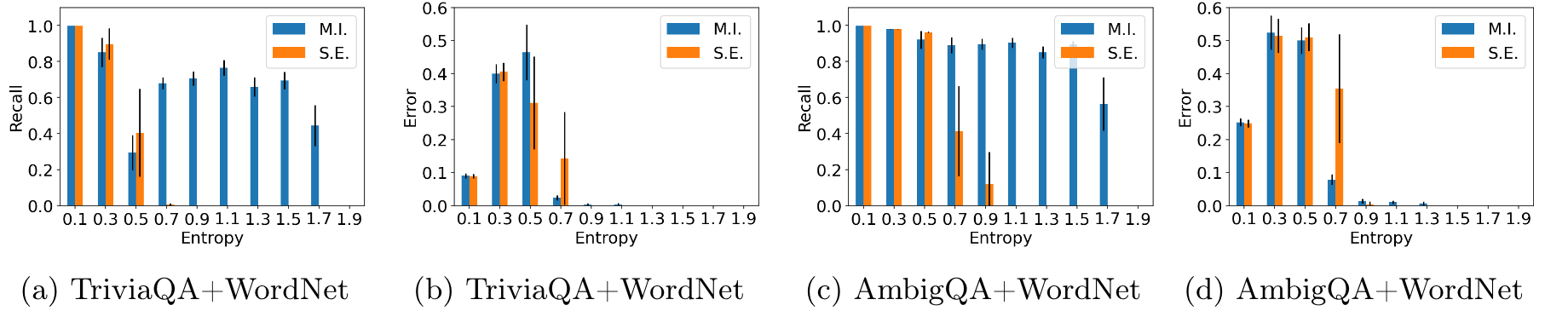
- "파리는 어느 나라의 수도인가?"라는 질문에 대해 모델이 "프랑스"라는 일관된 답을 여러 번 제공한다면, 이 질문의 엔트로피는 낮음.
- 모델이 이 질문에 대해 높은 확신을 가지고 있으며, 응답의 불확실성이 거의 없다
- S.E. 방법은 낮은 엔트로피 쿼리에 대해서는 제안된 방법과 유사한 재현율 및 오류율을 보였으나, 높은 엔트로피 쿼리에 대해서는 재현율이 훨씬 낮음
Conclusion
-
LLM의 truthfulness를 평가하는 지표로 epistemic uncertainty를 고려함.
-
증명가능한 하한을 제공하는 Mutual-information based uncertainty estimator를 제안.
-
여러가지 답변의 결합분포를 고려함으로써, aleatoric, epistemic uncertainty를 분리하고, 이를 통해 epistemic uncertainty를 단독으로 사용하는 방법으로, 전체를 사용하는 first order method보다 좋은 성능을 보임.
-
vision에서도 같은 개념으로 사용될 수 있는가 ?
-
Uncertainty , Unlearning이 연관되어 있지 않을까?
-
diffusion uncertainty.
- Epistemic, aleatoric를 어떻게 정의해야 할까?
-
언어에 따른 aleatoric uncertainty가 다른가?
