Chapter 2 Descriptive Statistics:
Tabular and Graphical Presentations
Categorical data 관점
Frequency Distribution
- 도수분포표(Frequency Distribution)는 서로 겹치지 않는 여러 구간에서 각 항목의 빈도(또는 수)를 보여주는 데이터의 요약
- 이는 원본 데이터만으로는 빠르게 얻을 수 없는 데이터에 대한 통찰력(insights)을 제공하기
이해를 돕기 위한 자료
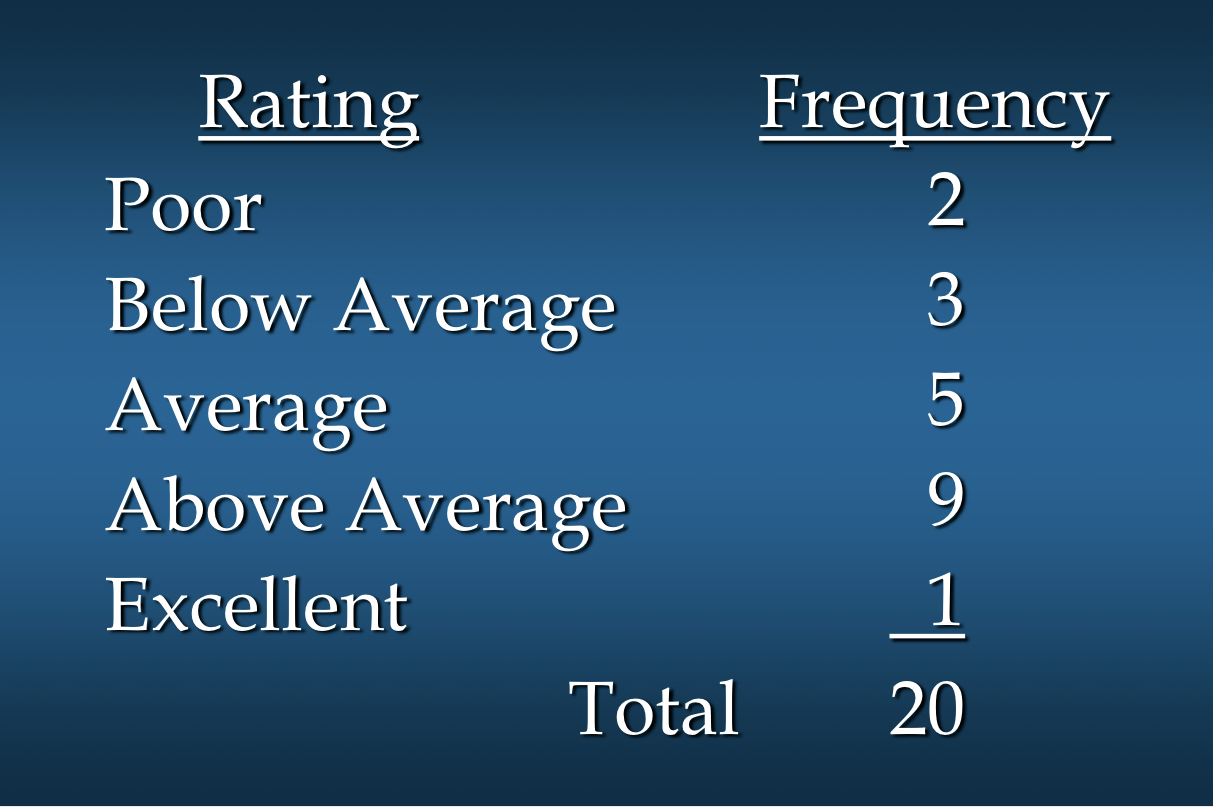
Marada Inn에 머무는 손님들에게 숙박 시설의 질을
훌륭하다, 평균 이상이다, 보통이다, 평균 이하이다, 혹은 나쁘다로
평가하도록 요청하였다. 20명의 표본에서 제공된 평가는 다음과 같다:
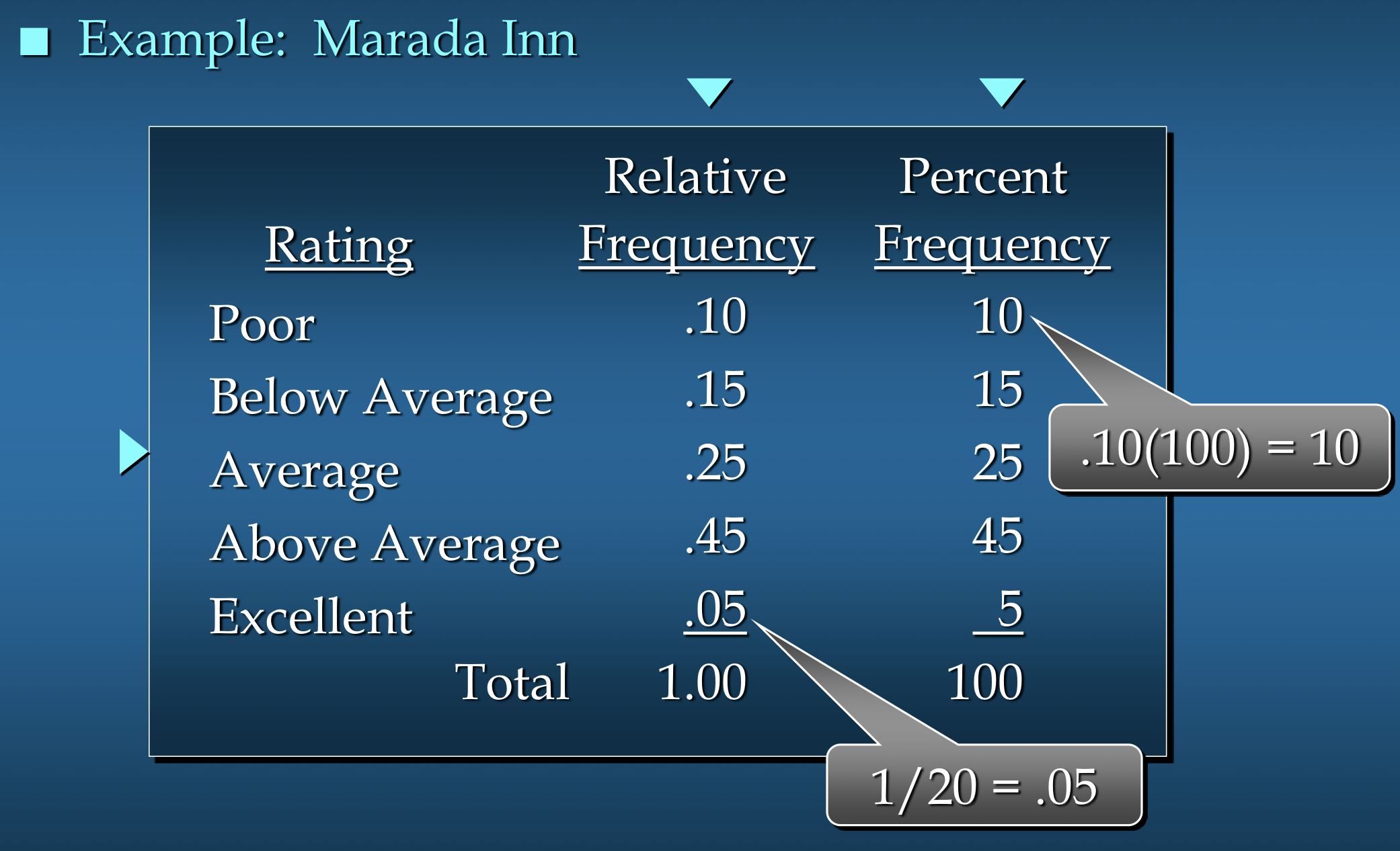
상대도수분포(Relative Frequency Distribution)
- 상대도수분포(Relative Frequency Distribution)는 클래스에 속하는 데이터 항목의 총 개수에 대한 분수 또는 비율
- 각 클래스의 상대도수를 보여주는 데이터 집합의 표적 요약
백분율 빈도 분포(Percent Frequency Distribution)
- 클래스의 백분율 빈도는 상대 빈도에 100을 곱한 것
- 백분율 빈도 분포는 각 클래스의 백분율 빈도를 보여주는 데이터 집합의 표 요약
이해를 돕기 위한 자료
- 추가 예시
학생들의 수학 점수과 다음과 같다:
[60, 75, 80, 85, 90, 95, 95, 100, 100, 100]
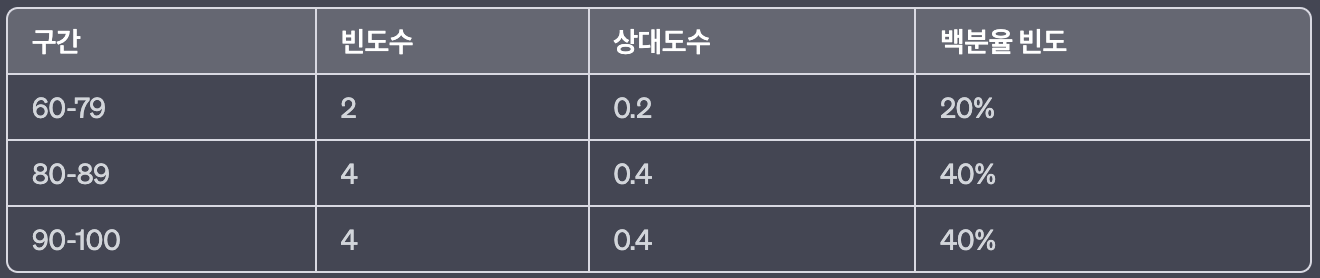여기서, 상대도수 = 빈도수 / 데이터 총 개수
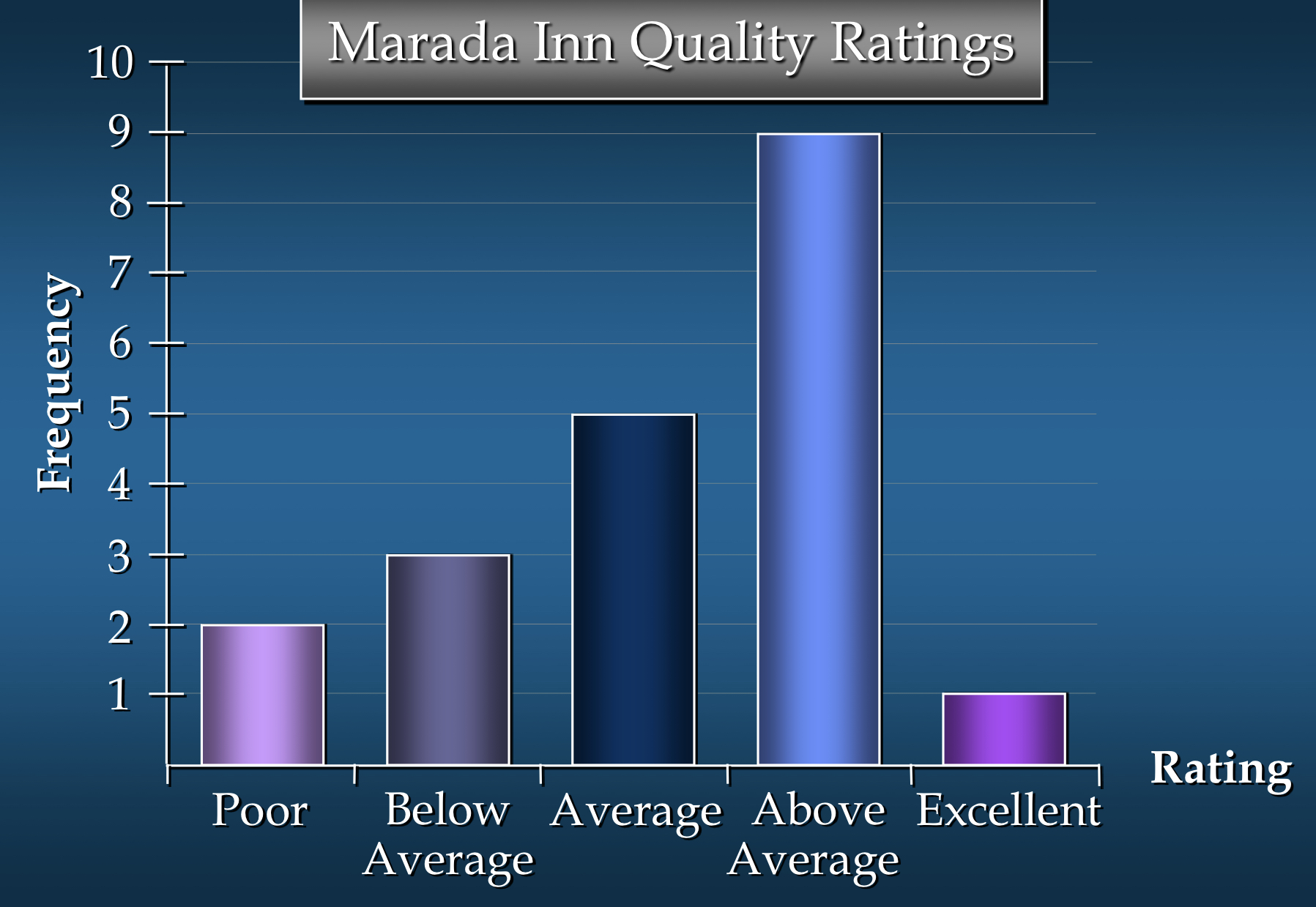
막대 그래프(Bar Chart)
- 막대 그래프(bar chart)는 질적 데이터(qualitative data)를 시각적으로 나타내기 위한 그래픽 기법
- 하나의 축(보통 가로축)에는 각 범주(category)를 나타내는 레이블을 지정
- 다른 축(보통 세로축)에는 도수(frequency), 상대도수(relative frequency), 또는 백분율 빈도(percent frequency) 척도를 사용
- 각 범주 레이블 위에 고정 폭의 막대를 그리고 높이를 적절하게 확장
- 막대는 각 범주가 별개의 범주임을 강조하기 위해 분리
원형 그래프(Pie Chart)
- 원형 그래프(Pie Chart)는 범주형 데이터(categorical data)의 상대도수(relative frequency)와 백분율 빈도(percent frequency distributions)를 표시하는 데 자주 사용되는 그래픽 기기
- 먼저 원을 그린 다음, 각 범주에 해당하는 상대도수(relative frequency)를 사용하여 원을 분할
- 원에는 360도가 있으므로, 상대도수가 0.25인 범주는 원에서 0.25(360) = 90도를 차지
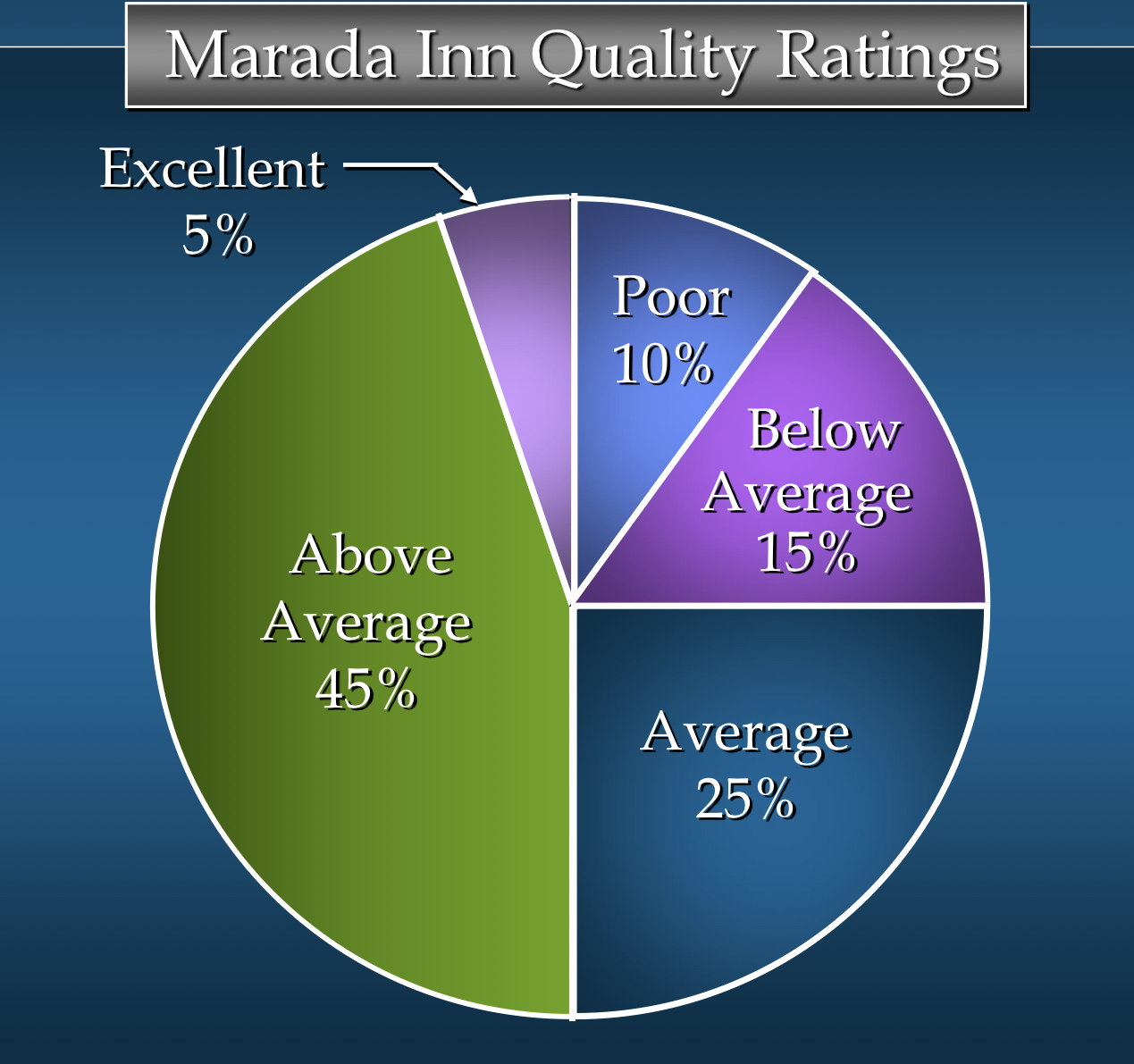
- 원형 그래프로부터 얻는 인사이트
- 조사 대상 고객의 절반이 "평균 이상" 또는 "매우 좋음"으로 마라다를 평가 (파이 차트 왼쪽을 보면)
-> 이것은 매니저를 기쁘게 할 수 있을 것 - "매우 좋음" 등급을 준 고객 한 명당 "나쁨" 등급을 준 고객이 두 명 (파이 차트 상단을 보면)
-> 이것은 매니저를 불평케 할 것
- 조사 대상 고객의 절반이 "평균 이상" 또는 "매우 좋음"으로 마라다를 평가 (파이 차트 왼쪽을 보면)
Quantitative data 관점
Frequency Distribution
이해를 돕기 위한 자료
Hudson Auto Repair:
Hudson Auto의 매니저는 자신들의 차량 정비소에서 수리에 사용되는 부품 비용에 대해 더 잘 이해하기 위해,
정비 서비스 중인 50 건의 고객 인보이스를 조사합니다.
부품 비용은 가장 가까운 달러로 반올림되어 다음 슬라이드에 나열되어 있습니다.
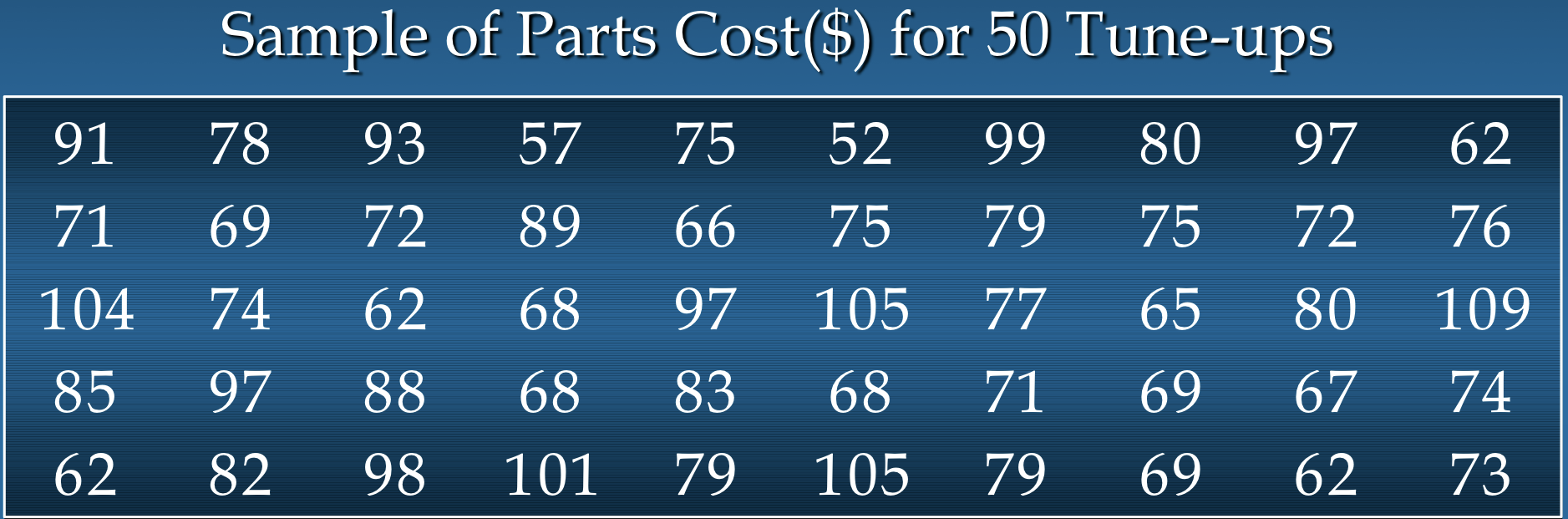
양적 자료(Quantitative data)를 이용한 도수분포표를 만들기 위해 필요한 세 가지 단계:
- 중복되지 않는 클래스의 수를 결정
- 각 클래스의 폭을 결정
- 클래스 한계를 결정
클래스 수를 결정하는 지침
- 5에서 20개 사이의 클래스를 사용합니다.
- 데이터의 요소 수가 많을수록 더 많은 클래스가 필요합니다.
- 요소 수가 적은 데이터는 적은 수의 클래스가 필요합니다.
각 클래스의 폭을 결정하는 지침
- 동일한 폭의 클래스를 사용하세요.
- 근사 클래스 폭 = (최대 데이터 값 - 최소 데이터 값) / 클래스 수
즉, 최대 데이터 값과 최소 데이터 값의 차이를 클래스 수로 나눈 것이 각 클래스의 폭이 되도록 하는 것
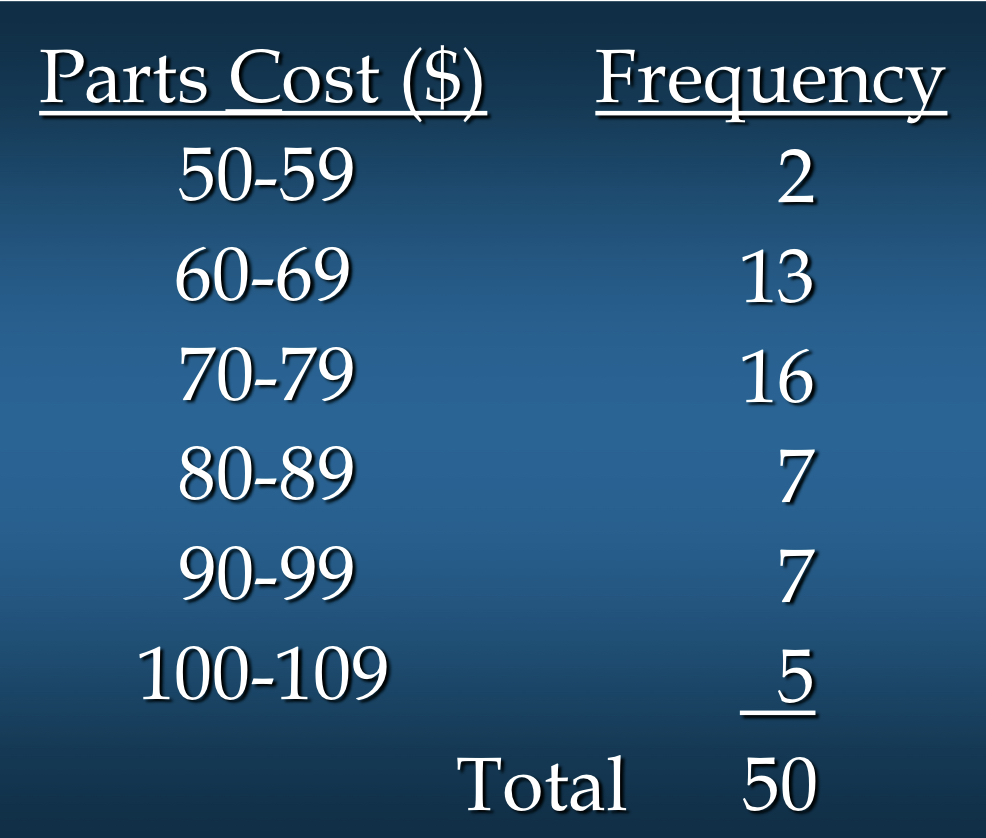만약, 우리가 6개의 class들을 골랐다고 가정:
근사 클래스 폭(Approximate Class Width) = (109 - 52) / 6 = 9.5 = 10
상대도수분포(Relative Frequency Distribution) & 백분율 빈도 분포(Percent Frequency Distribution)
이해를 돕기 위한 자료
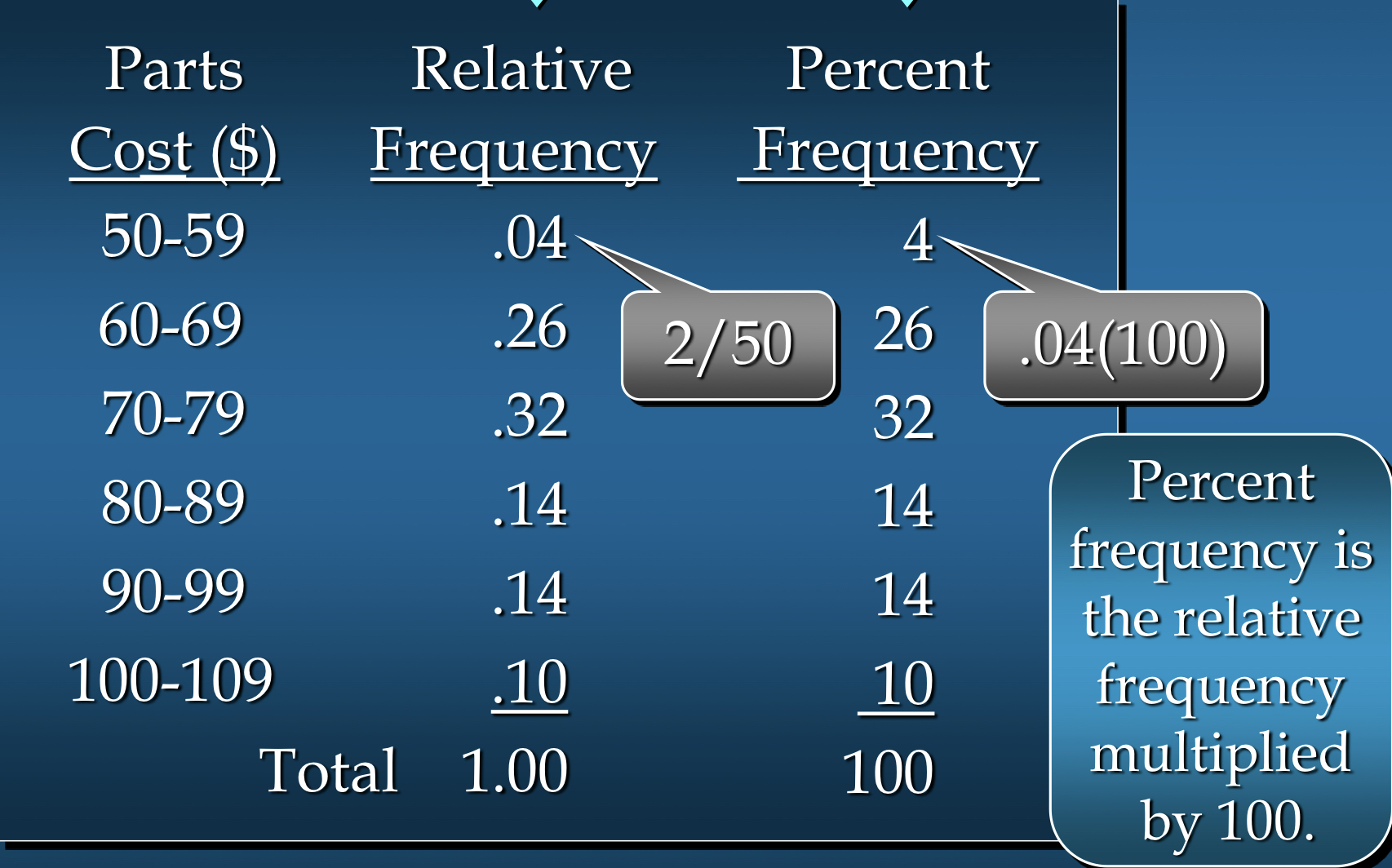
백분율 빈도수 분포에서 얻은 인사이트:
- 부품 비용이 $50-59 범주에 속하는 것은 전체 중 4%뿐
- 부품 비용의 30%가 $70 미만
- 부품 비용의 가장 큰 비율인 32%(거의 1/3)가 $70-79 범주에 속함
- 부품 비용의 10%는 $100 이상
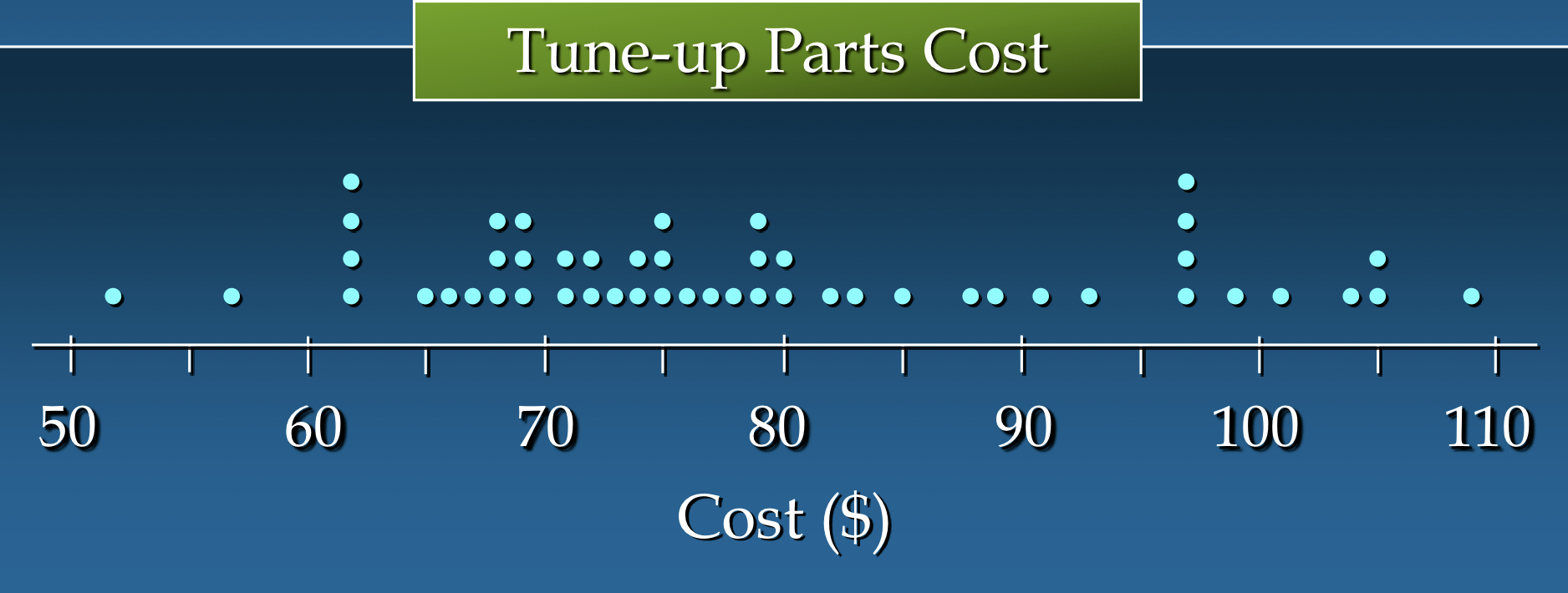
도트 플롯(Dot Plot)
- 데이터를 시각적으로 요약하는 가장 간단한 그래픽 요약 방법 중 하나
- 수평축은 데이터 값의 범위를 보여 줌
- 그런 다음 각 데이터 값은 축 위에 위치한 점으로 나타냄
이해를 돕기 위한 자료
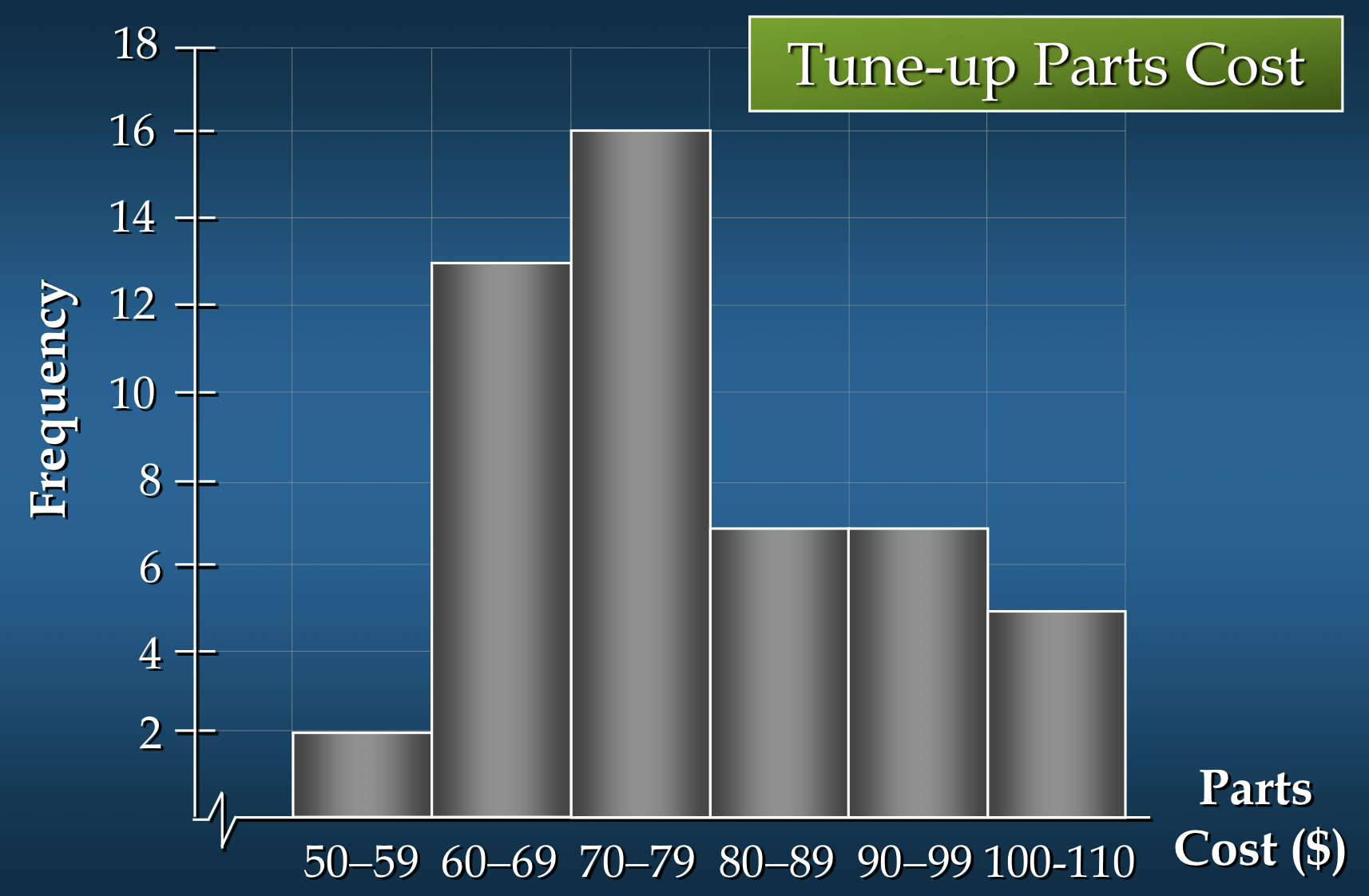
히스토그램(Histogram)
- 양적 자료(quantitative data)를 그래프로 나타내는 일반적인 방법 중 하나
- 변수의 범위가 수평축(horizontal axis)에 표시
- 각 구간에 해당하는 사각형을 그림으로써, 사각형의 높이가 해당 구간의 빈도, 상대도수(relative frequency) 또는 백분율 빈도(percent frequency)와 대응
- 막대 그래프와는 달리, 히스토그램에서는 인접한 클래스의 사각형 사이에 자연스러운 간격이 없음
이해를 돕기 위한 자료
히스토그램의 왜도를 보여주는 경우
-
대칭인 경우(Symmetric)
- 왼쪽 꼬리와 오른쪽 꼬리가 거울상의 이미지인 경우
- 예시:
사람들의 키와 몸무게
-
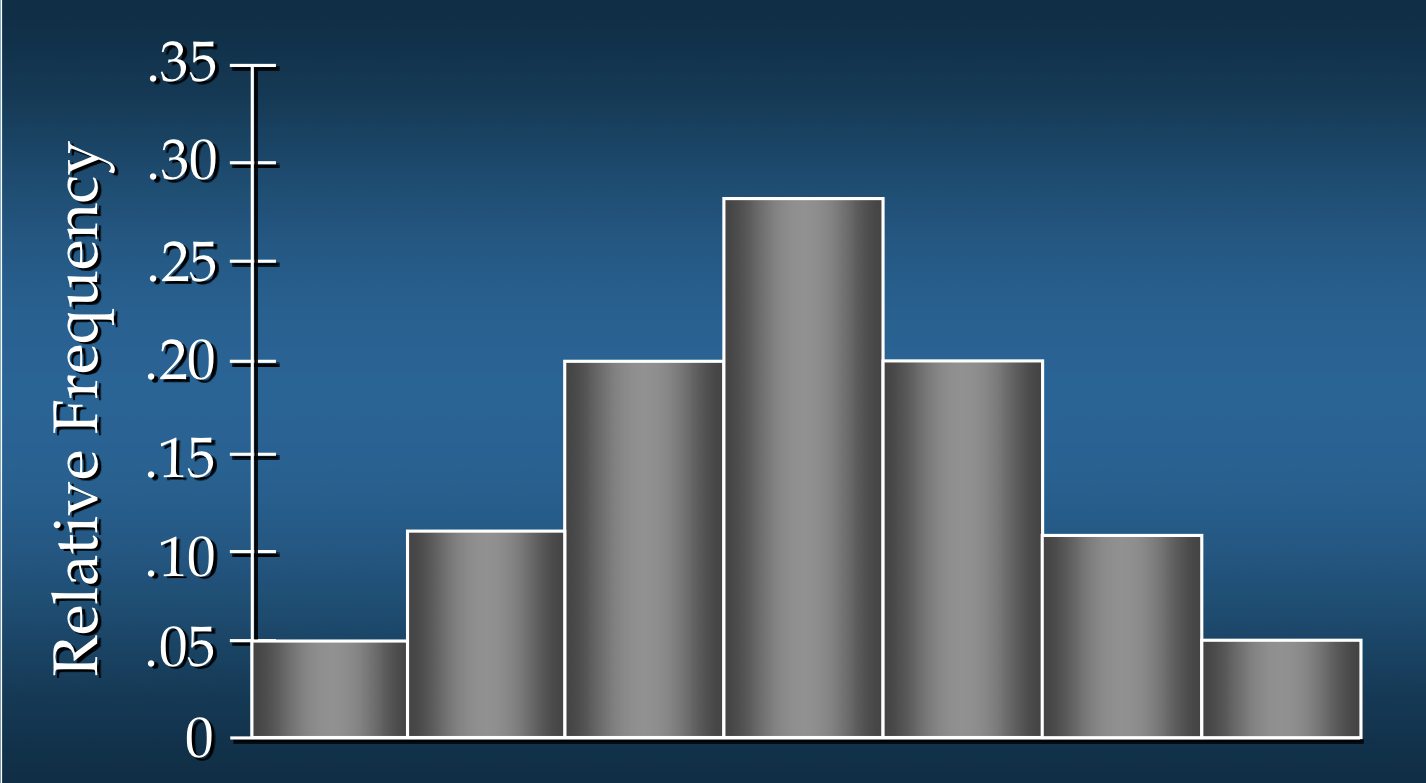
중간 정도 왼쪽 치우침(Moderately Skewed Left)
- 왼쪽에 긴 꼬리가 있는 모양
- 예시:
시험 성적
-
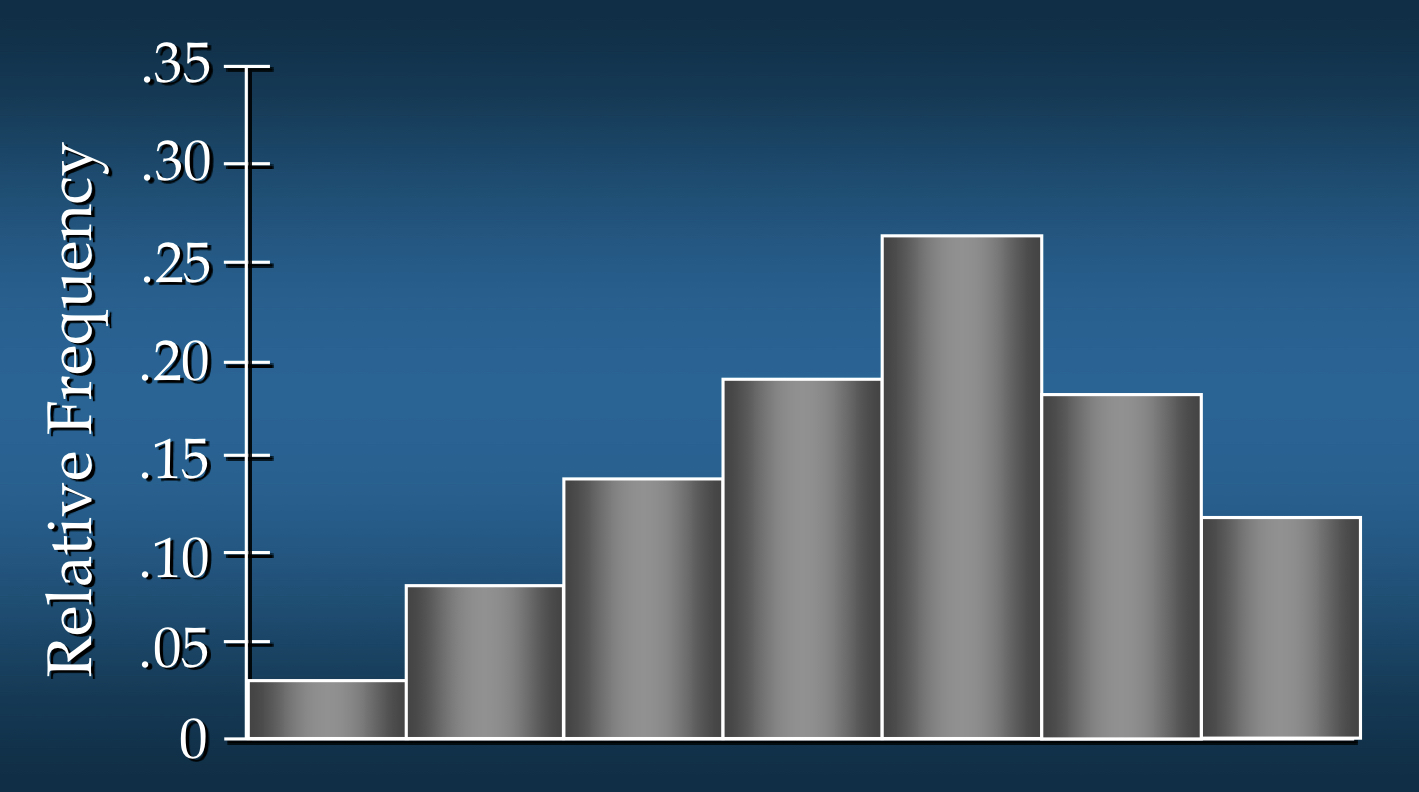
종모양이 오른쪽으로 길게 늘어진 분포(Moderately Right Skewed)
- 오른쪽으로 길게 늘어진 꼬리가 있음
- 예시:
부동산 가치
-
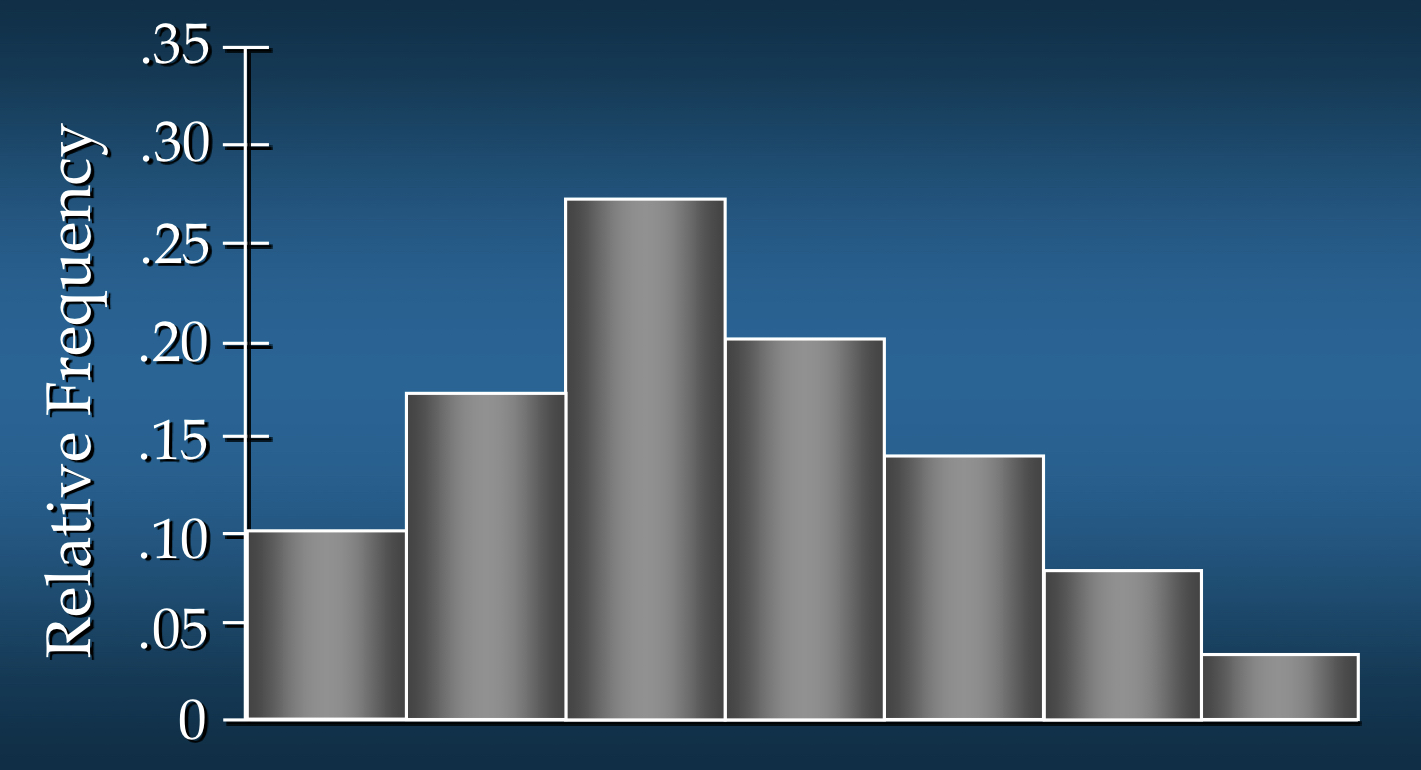
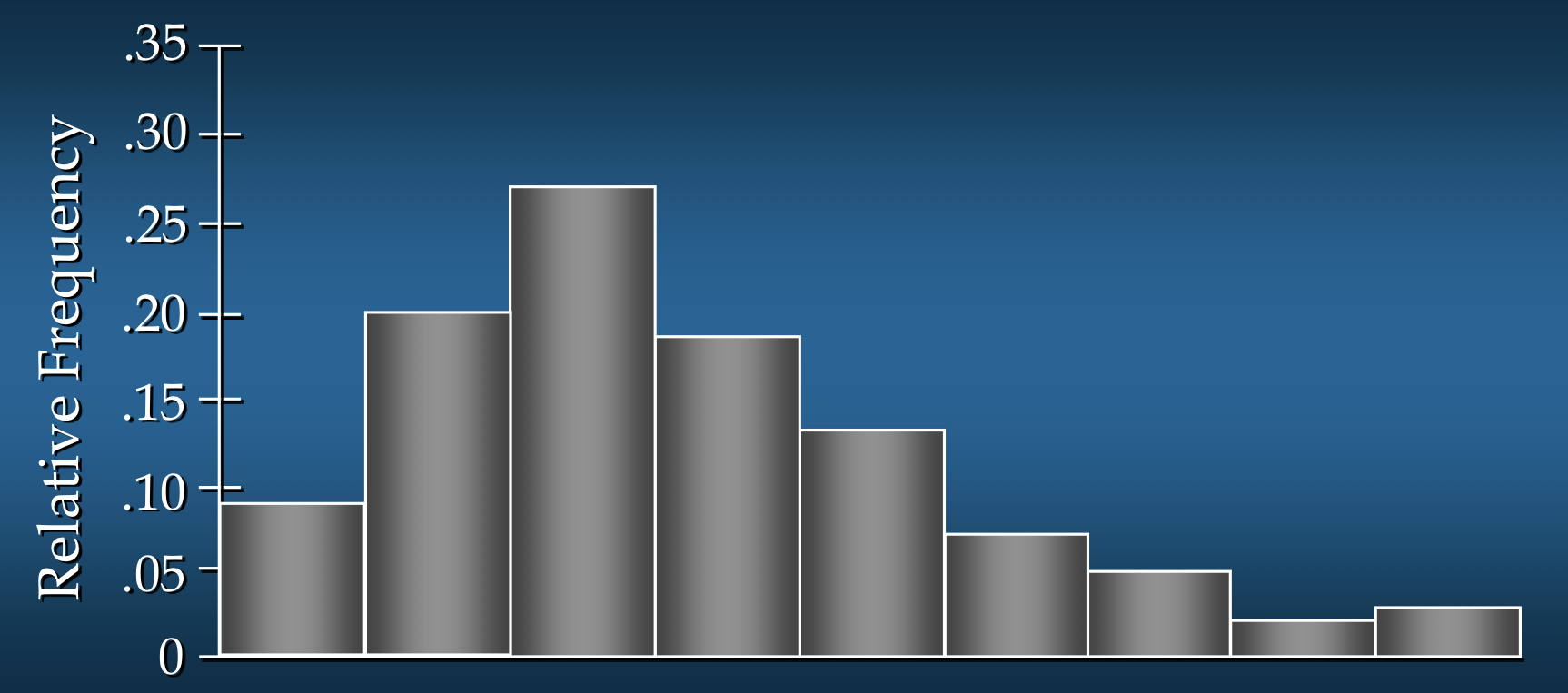
좌우 비대칭이 심한 경우(Highly Skewed Right)
- 오른쪽으로 매우 긴 꼬리를 가진 경우
- 예시:
경영진 연봉
누적 분포(Cumulative Distributions)
-
누적 도수 분포(Cumulative frequency distribution)
각 계급 상한값보다 작거나 같은 값의 항목 수를 보여 줌 -
누적 상대 도수 분포(Cumulative relative frequency distribution)
각 계급 상한값보다 작거나 같은 값의 항목 비율을 보여 줌 -
누적 백분율 도수 분포(Cumulative percent frequency distribution)
각 계급 상한값보다 작거나 같은 값의 항목 백분율을 보여 줌
이해를 돕기 위한 자료
오지브(Ogive)
- 오지브는 누적 분포의 그래프(cumulative distribution)
- 수평 축에는 데이터 값이 표시
- 수직 축에는 다음 중 하나가 표시
- 누적 빈도(cumulative frequencies)
- 누적 상대 빈도(cumulative relative frequencies)
- 누적 백분율 빈도(cumulative percent frequencies)
- 각 클래스의 빈도(위에서 언급한 중 하나)가 점으로 표시
- 그림에서 표시된 점들은 직선으로 연결
이해를 돕기 위한 자료
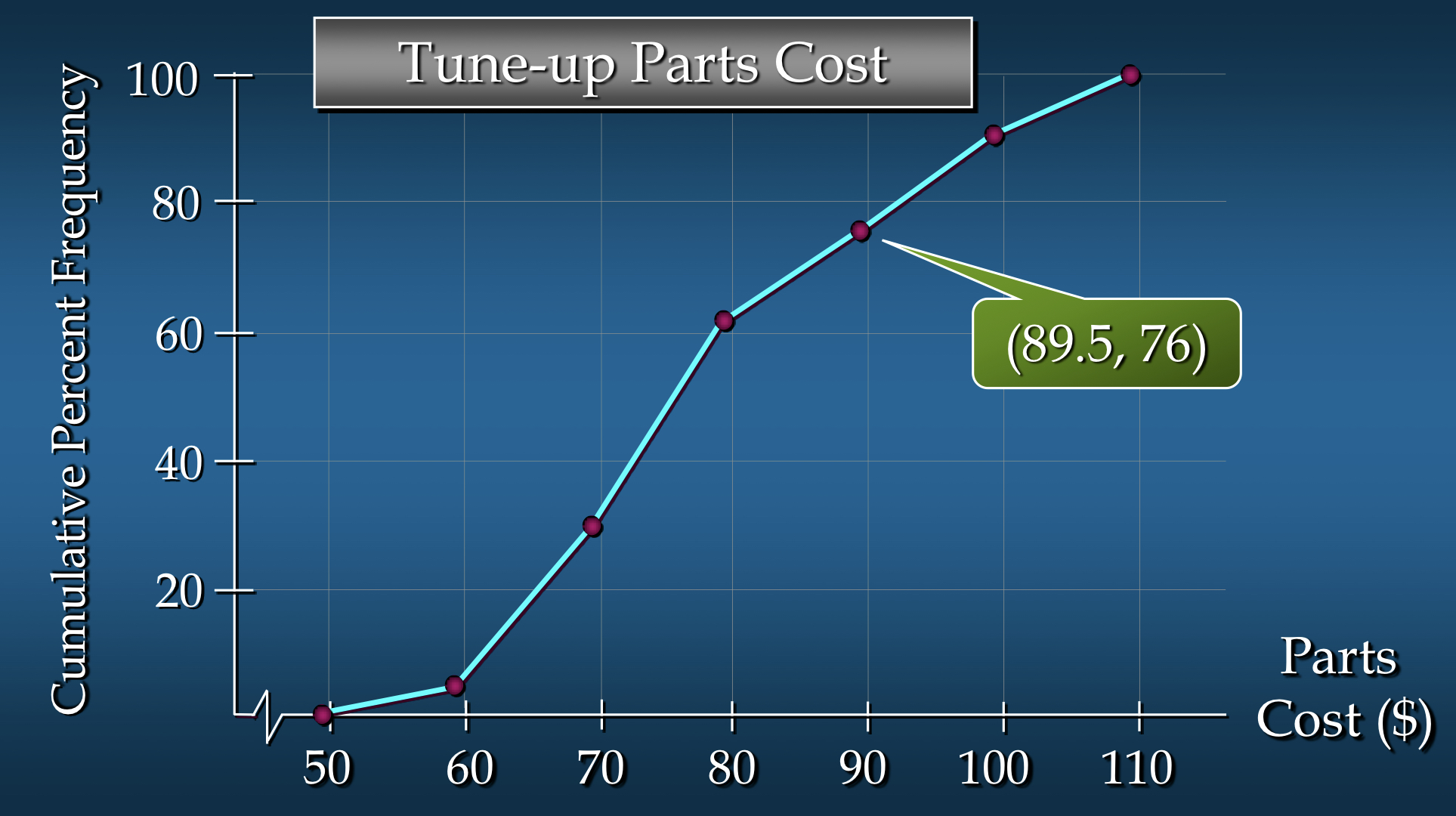
부품 비용 데이터의 클래스 한계가 50-59, 60-69 등이므로 59에서 60, 69에서 70 등 사이에 1단위 간격이 나타남
이러한 간격은 클래스 한계의 중간 지점에 점을 표시하여 제거
따라서, 50-59 클래스에 대해 59.5, 60-69 클래스에 대해 69.5 등을 사용
- 공백 발생 이유??
예를 들어, 50-59 구간에는 53, 56, 59 등의 값이 속하는데, 이 구간의 상한값이 59이므로 59보다 큰 값은 다음 구간인 60-69에 속하게 됨
이 경우, 59와 60 사이에 값이 있을 수 있지만 해당 값은 어느 구간에도 속하지 않기 때문에 공백이 생김
이를 해결하기 위해 구간의 중간값을 사용하면 이러한 공백을 없앨 수 있음
