머신러닝 기초 - 주성분분석 (Principal Component Analysis, PCA)

1. 차원축소의 필요성

• 데이터는 일반적으로 수많은 특성(변수)으로 표현됨
• 차원이 커질수록 계산 복잡성과 자원 소모가 증가 → 분석/학습 효율 저하
• 차원 축소 시 이점:
  • 계산 속도 향상
  • 시각화 가능
  • 노이즈 제거 및 모델 성능 개선

📌 예시 (iris 데이터 4차원 → 2차원)

from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import pandas as pd

iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['target'] = iris.target

plt.scatter(df['sepal length (cm)'], df['sepal width (cm)'], c=df['target'])
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.title('Iris Dataset 2D Projection Example')
plt.show()

2.차원축소 방법

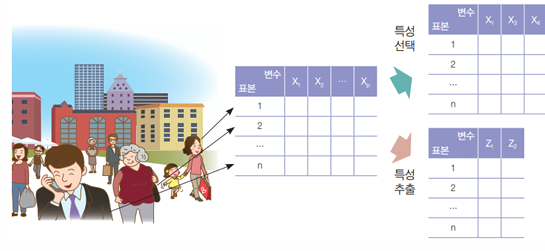
1. 특성 선택 (Feature Selection)

• 유의미한 변수만 선택
• 분산이 작거나 상관계수가 높은 변수 제거

2. 특성 추출 (Feature Extraction)

• 기존 변수를 변환해 새로운 변수(주성분, PC)를 생성
• PCA는 대표적인 특성 추출 방법

3. PCA 기본원리

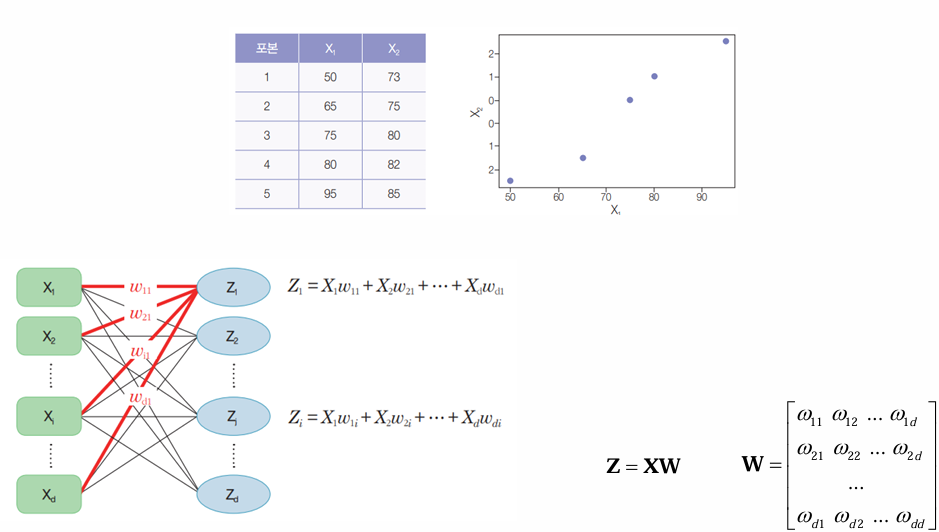
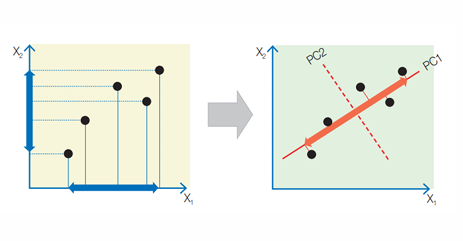
• 입력 변수를 선형 변환하여 새로운 직교 좌표계(주성분) 생성
• 분산이 큰 방향(정보가 많은 방향)부터 주성분을 선택
• 공분산 행렬의 고유벡터 → 주성분 방향
• 고윳값의 크기 → 분산 크기

📌 예시 (PCA 적용)

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

# 데이터 스케일링
X = StandardScaler().fit_transform(iris.data)

# PCA 2차원으로 축소
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

print("설명된 분산 비율:", pca.explained_variance_ratio_)

4. PCA 단계별 절차

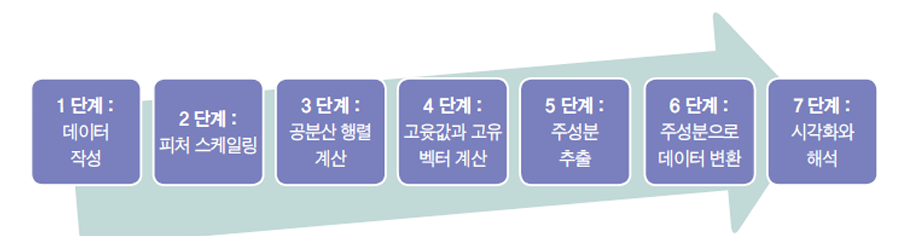
1. 데이터 표준화 (평균=0, 분산=1)
2. 공분산 행렬 계산
3. 고유값/고유벡터 추출
4. 가장 큰 고유값 방향(주성분) 선택
5. 데이터 변환 (Projection)

📌 시각화 예제

import matplotlib.pyplot as plt

plt.figure(figsize=(8,6))
plt.scatter(X_pca[:,0], X_pca[:,1], c=iris.target, cmap='viridis')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.title('Iris Dataset PCA (2D)')
plt.colorbar(label='Species')
plt.show()

6. 활용 사례

• 이미지 데이터 (MNIST)
  • 28×28 = 784차원 → 수십 차원으로 축소 가능
  • 학습 시간 단축 & 노이즈 감소
• 보스턴 주택 가격 예측
  • 13개 독립변수 → 일부 주성분만 활용하여 효과적 예측

📌 MNIST 예제 (차원축소)

from sklearn.datasets import fetch_openml

mnist = fetch_openml('mnist_784', version=1)
X_mnist, y_mnist = mnist.data, mnist.target

pca = PCA(n_components=50)  # 784 → 50차원
X_mnist_pca = pca.fit_transform(X_mnist)

print("원본 차원:", X_mnist.shape)
print("축소된 차원:", X_mnist_pca.shape)

7. PCA 결과 해석

• 설명된 분산 비율 (Explained Variance Ratio)
  → 각 주성분이 원본 데이터의 정보를 얼마나 보존하는지 나타냄

• 로딩(Loading)
  → 각 원본 변수가 주성분에 기여하는 정도

print("주성분 로딩:\n", pca.components_)

8. 핵심 요약

8. 핵심 요약

• 차원축소는 계산 효율과 시각화, 성능 개선에 중요
• PCA는 특성 추출 기반 차원축소 기법으로, 공분산 행렬의 고유벡터를 활용
• 데이터의 분산을 최대한 보존하면서 차원을 줄임
• 주요 지표: 설명된 분산 비율, 로딩
• 응용: 이미지 인식(MNIST), 데이터 시각화(Iris), 회귀 예측(보스턴 주택가격)