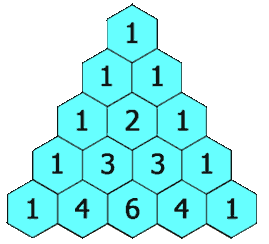
예제: Pascal's Triangle II
문제
Given a non-negative index k where k ≤ 33, return the k'th index row of the Pascal's triangle.Note that the row index starts from 0.
In Pascal's triangle, each number is the sum of the two numbers directly above it.Example:
Input: 3 Output: [1,3,3,1]Follow up:
Could you optimize your algorithm to use only O(k) extra space?
풀이
k번째의 파스칼 삼각형의 행의 값을 찾는 문제이다.
피보나치 수열로 익숙한 문제이지만, 마지막에 use only O(k) extra space가 매우 압박스럽다.
따라서, vector(rowIndex + 1) 만큼의 메모리를 할당하지 말라는 소리로 이해하면 될 것 같다.
필자는 처음에 아래 CASE1번과 같이 풀었는데, 앞에서부터 피보나치 행렬을 만들려다 보니 tmp라는 벡터를 할당했다 해제하는 방법을 사용한다. 그러나 이 방법은 뭔가 좀 편법? 같은 느낌이 든다.
그래서 찾아보다가 CASE2번과 같은 아주 좋은 방법을 발견했는데, 피보나치 행렬을 뒤에서부터 만드는 것이다. 이렇게 하면 다른 메모리를 할당할 필요도 없이 깔끔하게 해결된다.
전체적인 소스코드는 아래와 같다.
소스 코드
/* CASE1 */
class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<int> res(rowIndex + 1);
res[0] = 1;
for (int i = 1; i <= rowIndex; i++) {
vector<int> tmp(res);
for (int j = 1; j < i; j++) {
res[j] = tmp[j - 1] + tmp[j];
}
res[i] = 1;
}
return res;
}
};
/* CASE2 */
class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<int> res(rowIndex + 1, 0);
res[0] = 1;
for (int i = 1; i <= rowIndex; i++) {
for (int j = i; j >= 1; j--) {
res[j] = res[j] + res[j - 1];
}
}
return res;
}
};풀이 후기
단지 피보나치 행렬을 만드는 순서를 앞에서 뒤로 바꾸었을 뿐인데, 코드가 훨씬 깔끔해지는 느낌을 받을 수 있다. 조금만 다른 시각으로 접근해도 코드를 훨씬 깔끔하게 만들 수 있다. 간단하지만 참 어려운 문제이다.