알고리즘 문제해결 전략 Chapter 08 - ASYMTILING(C++)

포타토·2019년 12월 2일

알고리즘

목록 보기

2/76

예제: 비대칭 타일링

문제

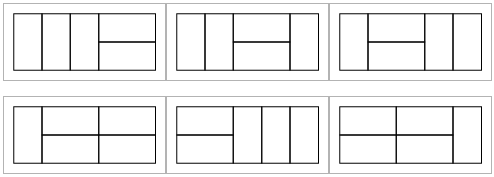
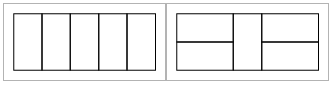
그림과 같이 2 n 크기의 직사각형을 2 1 크기의 타일로 채우려고 합니다. 타일들은 서로 겹쳐서는 안 되고, 90도로 회전해서 쓸 수 있습니다. 단 이 타일링 방법은 좌우 대칭이어서는 안 됩니다. 위 그림은 2 * 5 크기의 직사각형을 채우는 비대칭 타일링 방법 6가지를 보여줍니다. 다음의 2가지는 좌우대칭이기 때문에 세지 않습니다.

n 이 주어질 때 가능한 비대칭 타일링 방법의 수를 계산하는 프로그램을 작성하세요. 방법의 수는 매우 클 수 있으므로, 1,000,000,007 로 나눈 나머지를 출력합니다.

입력
입력의 첫 줄에는 테스트 케이스의 수 C (1 <= C <= 50) 가 주어집니다. 그 후 각 줄에 사각형의 너비 n (1 <= n <= 100) 이 주어집니다.

출력
각 테스트 케이스마다 한 줄에 비대칭 타일링 방법의 수를 1,000,000,007 로 나눈 나머지를 출력합니다.

예제 입력
3
2
4
92
```
__예제 출력__
```
0
2
913227494
```

풀이

이 문제는 두 가지 방법 정도가 떠올랐는데,
1. 전체 타일링 방법의 수(2 x n) - 반절의 타일링 방법의 수(2 x (n / 2))
2. 대칭 형태를 제외하며 타일링 방법 count

필자는 1번 방법이 더 수월해 보였기 때문에, 1번 방법을 택하였다.

1) 전체 타일링 방법의 수(2 x n)

필자는 이 문제를 두 번째로 풀었는데, 이전 코드보다는 좀 더 효율적이 되었다고 생각하여 해당 풀이를 수정한다. 전체 타일링 방법의 수는 이전에 풀었던 문제인 TILING2와 동일하다.

int tiling(int n) {
	if (n <= 1) return 1;

	int& res = cache[n];
	if (res != -1) return res;

	return res = (tiling(n - 1) + tiling(n - 2)) % MOD;
}

2) 반절의 타일링 방법의 수(2 x (n / 2))

n이 홀수일 경우와 짝수일 경우가 다른데, 홀수인 경우는 n / 2 지점에서(n = 5일 경우, idx = 2인 지점) 2 x 1짜리 타일을 한 개 깔아야 대칭이 된다.
n이 짝수인 경우는, n / 2 지점에서(n = 6인 경우, idx = 3인 지점) 2 x 1짜리 타일을 한개 깔거나, 1 x 2 타일을 두 개 깔때 대칭이 된다.

즉, 아래 그림과 같을 경우만 대칭이 된다.

x x | x x
x x | x x

x x ㅡ ㅡ x x
x x ㅡ ㅡ x x

x x | | x x
x x | | x x

우리는 이미 tiling() 함수를 통해서 모든 경우의 수를 구해놓았기 때문에,
짝수일 경우는 tiling(n) - tiling(n/2) - tiling(n/2 - 1),
홀수일 경우는 tiling(n) - tiling(n/2)를 해주면 되겠다.

다만 함정을 조심한다.
mod 연산을 하므로, tiling(n)이 tiling(n/2)보다 작을 수 있기 때문이다.

항상 이런 실수가 다 풀어놓고 틀리게 한다..
음수일 경우를 대비해서, -연산이 있다면 mod 연산의 제수를 더해준다.

전체적인 소스코드는 아래와 같다.

소스 코드

#include<iostream>
#include<cstring>

using namespace std;

const int MOD = 1000000007;
int cache[101];

int tiling(int n) {
	if (n <= 1) return 1;

	int& res = cache[n];
	if (res != -1) return res;

	return res = (tiling(n - 1) + tiling(n - 2)) % MOD;
}

int asymtiling(int n) {
	if (n % 2 == 1) {
		return (tiling(n) - tiling(n / 2) + MOD) % MOD;
	}
	else {
		return ((tiling(n) - tiling(n / 2) + MOD) % MOD - tiling(n / 2 - 1) + MOD) % MOD;
	}
}

int main() {

	int testCase;
	cin >> testCase;

	for (int tc = 0; tc < testCase; tc++) {
		memset(cache, -1, sizeof(cache));
		int n;
		cin >> n;

		cout << asymtiling(n) << endl;
	}

	return 0;
}