해싱(Hashing) : 다양한 크기의 입력값을 고정된 크기의 출력값으로 생성해 내는 과정
해시 함수 : 어떠한 크기의 입력이 들어와도 동일한 크기의 출력을 뱉는 함수 (SHA-256 : 항상 256비트 길이 값 출력, SHA-1 : 160 비트 값 출력)

🔗 블록체인에서 해싱의 역할

1. 해시값을 사용해 익명성 보장

공개키를 해싱하여 지갑 주소로 사용 → 지갑의 주인이 누구인지 알 수 없음. (암호화된 지갑 주소, 송금, 잔액은 확인 가능)

2. 무결성 검증

1) 이전 블록의 값을 해싱한 값을 사용해 이전 블록을 가리킴. → 이전 블록을 해싱한 값이 달라진 경우 이전 블록에 위변조가 일어났음을 알 수 있음.

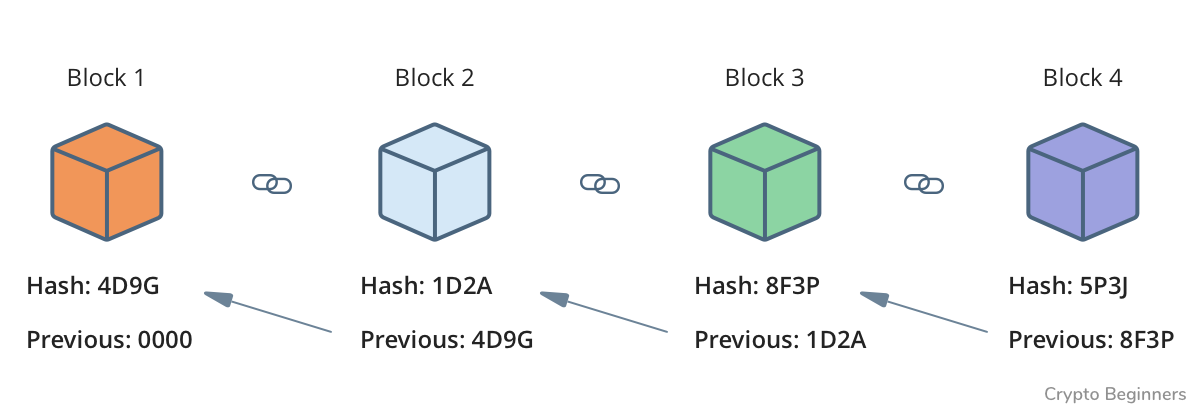
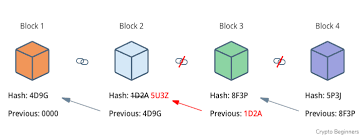
2) 하나의 블록에 저장된 모든 트랜잭션을 머클 트리 알고리즘으로 하나의 해시값으로 저장. 트랜잭션이 하나라도 변한 경우, 블록에 저장된 해시값도 변경됨

→ 모든 데이터를 대조할 필요 없이, 고정된 크기의 해시값을 비교하면 되기 때문에 많은 양의 데이터를 저장하거나 기억할 필요 없이 무결성 검증 가능.

3. 해시값을 사용해 채굴 노드를 정한다.

PoW 방식에서 특정 조건을 만족하는 해시값을 만족하기 위해 입력 값인 논스(Nonce)를 찾는 노드가 블록을 만들 권한을 주고, 채굴에 대한 보상으로 비트코인을 제공함.

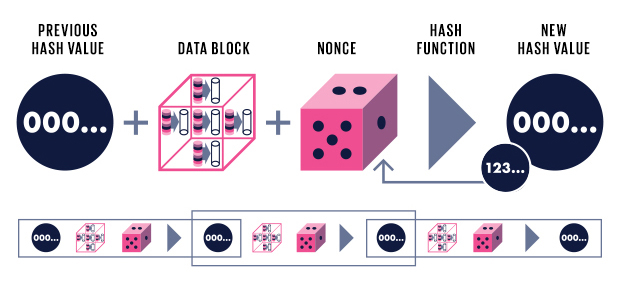
🔗 암호 해시 함수

암호 해시 함수의 안정성 평가 요소

1. 충돌 저항성

충돌이 발견되지 않는 상태

충돌: 서로 다른 입력값을 해시 함수에 넣었는데 동일한 출력값을 내뱉는 경우.

그러나 해시 함수의 충돌을 발견할 가능성은 매우 적음. (SHA-256의 경우의 수: 2^256)
그러나 충돌이 없는 해시 함수는 존재하지 않다. 충돌 저항성이 있다고 간주되는 해시 함수가 존재할 뿐.

2. 역상 저항성

해시 함수가 특정한 값을 출력하는 입력값을 찾을 확률이 매우 낮은 상태.

단방향 함수: 평문을 암호문으로 암호화만 할 수 있는 함수
양방향 함수: 평문을 암호화도 할 수 있고 암호문을 복호화도 할 수 있는 알고리즘

블록체인에서 사용되는 해시함수는 단방향 알고리즘을 사용하기 때문에, 해싱된 값을 이용하여 기존의 값을 찾기란 매우 어려움. 복호화하기 위해서는 수많은 무차별 대입을 시도해야 함.

따라서 데이터를 보호하는데 매우 유리. 메시지 원본을 공개하지 않고도 진위성 검증이 가능.

3. 제 2 역상 저항성

충돌 저항성과 역상 저항성이 복합적으로 작용한 경우로, 입력 값에 대해, 그 입력의 해시 값을 바꾸지 않으면서 입력을 변경하는 것이 계산상 어려운 상태.

제 2 역상 공격에 대해 안전해야 한다.

• 제 1 역상 공격(first preimage attack): 해시값이 주어져 있을 때, 그 해시값을 출력하는 입력값을 찾는다.
• 제 2 역상 공격(second preimage attack): 입력값이 주어져 있을 때, 그 입력과 같은 해시값을 출력하는 다른 입력값을 찾는다.