백준 1446 java : DP, 다익스트라

DP 카테고리와 다익스트라 카테고리 둘 다 있다. 처음 시도할 때는 DP 카테고리 위주로 풀이 중이었고, 최소비용 문제라 DP로 풀이가 가능하다고 생각했다. 다익스트라 카테고리에서도 동일한 문제 번호가 보여서 두 알고리즘으로 연습해 보겠다.

1차 DP 풀이

import java.util.Scanner;

public class bj1446 {
    static Scanner scanner = new Scanner(System.in);
    static int N, D;
    static int [][] shortCut;

    public static void main(String[] args) {
        inputData();
        System.out.println(findAnswerByDP());

        scanner.close();
    }

    public static void inputData(){
        System.out.println("inputData()");
        int i;

        N = scanner.nextInt();
        D = scanner.nextInt();
        shortCut = new int[N][3];
        for(i = 0; i < N; i++){
            shortCut[i][0] = scanner.nextInt();
            shortCut[i][1] = scanner.nextInt();
            shortCut[i][2] = scanner.nextInt();
        }
    }

    public static int findAnswerByDP(){
        System.out.println("findAnswerByDP()");
        int answer = 0;
        int [] DP = new int[D + 1];
        int i, j;

        //D로 가는데 필요한 거리 초기화//<- 0가는데 필요한 거리 0 ~ D가는데 필요한 거리 D...
        for(i = 0; i <= D; i++){
            DP[i] = i;
        }

        System.out.print("최초 이동거리 : ");
        for(i = 1; i <= D; i++){
            System.out.print(DP[i] + " ");
        }

        System.out.print("\n짧은 이동거리 : ");
        for(i = 1; i <= D; i++){//현재 위치
            DP[i] = Math.min(DP[i], DP[i-1] + 1);//지름길을 거쳐와서 이동거리가 줄었는지 확인
            for(j = 0; j < N; j++){//현재 위치가 지름길 사용 직후 위치와 동일하다면?
                if(shortCut[j][1] == i){
                    DP[i] = Math.min(DP[i], DP[shortCut[j][0]] + shortCut[j][2]);//지름길을 탄게 그대로 온거보다 짧은지 판단
                }
            }
            System.out.print(DP[i] + " ");
        }
        System.out.println();
        answer = DP[D];

        return answer;
    }
}

2차 다익스트라

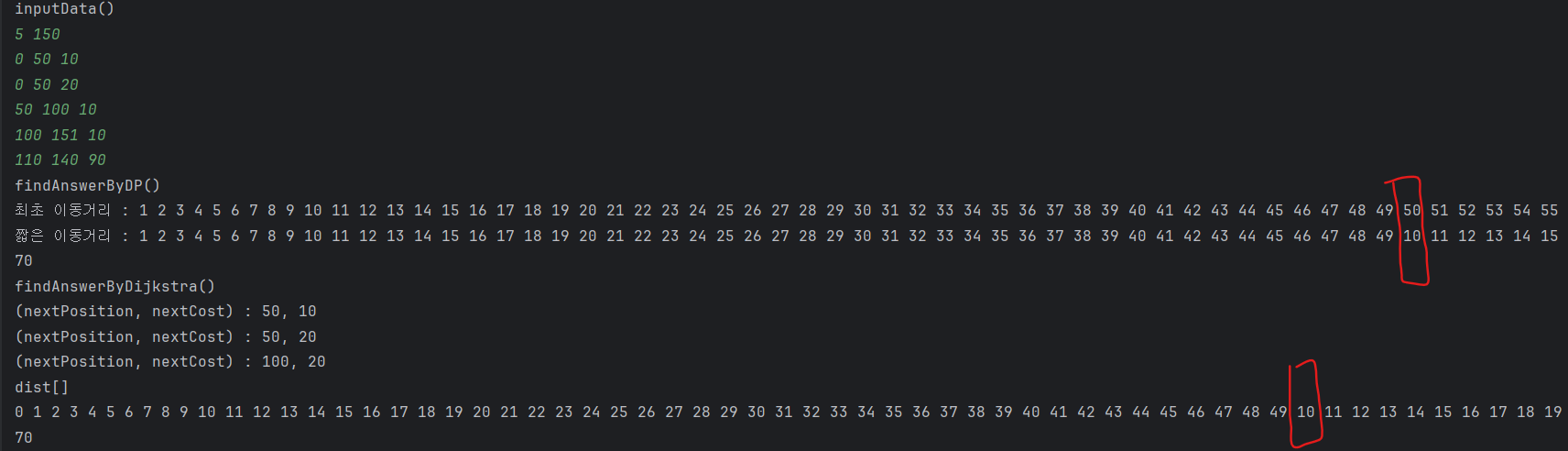
자원 소모 최적화를 안해서 메모리랑 시간이 더 사용된거 같다.

import java.util.*;

public class bj1446 {
    static Scanner scanner = new Scanner(System.in);
    static int N, D;
    static int [][] shortCut;
    static List<List<int[]>> graph = new ArrayList<>();

    public static void main(String[] args) {
        inputData();

        System.out.println(findAnswerByDP());
        System.out.println(findAnswerByDijkstra());

        scanner.close();
    }

    public static void inputData(){
        System.out.println("inputData()");
        int i, s, d, len;

        N = scanner.nextInt();
        D = scanner.nextInt();

        shortCut = new int[N][3];

        for (i = 0; i <= D; i++) {
            graph.add(new ArrayList<>());
        }

        for(i = 0; i < N; i++){
            s = scanner.nextInt();
            d = scanner.nextInt();
            len = scanner.nextInt();

            shortCut[i][0] = s;
            shortCut[i][1] = d;
            shortCut[i][2] = len;

            if (s <= D && d <= D && len < (d - s)) {
                graph.get(s).add(new int[]{d, len});
            }
        }
    }

    public static int findAnswerByDijkstra() {
        System.out.println("findAnswerByDijkstra()");
        PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[1]));
        int[] dist = new int[D + 1];
        Arrays.fill(dist, Integer.MAX_VALUE);
        dist[0] = 0;
        pq.add(new int[]{0, 0});

        while (!pq.isEmpty()) {
            int[] current = pq.poll();
            int position = current[0];
            int cost = current[1];

            if (cost > dist[position]) continue;

            for (int[] edge : graph.get(position)) {
                int nextPosition = edge[0];
                int nextCost = cost + edge[1];
                System.out.println("(nextPosition, nextCost) : " + nextPosition + ", " + nextCost);

                if (nextCost < dist[nextPosition]) {
                    dist[nextPosition] = nextCost;
                    pq.add(new int[]{nextPosition, nextCost});
                }
            }

            if (position + 1 <= D && cost + 1 < dist[position + 1]) {
                dist[position + 1] = cost + 1;
                pq.add(new int[]{position + 1, cost + 1});
            }
        }
        System.out.println("dist[]");
        for(int d : dist){
            System.out.print(d + " ");
        }
        System.out.println();

        return dist[D];
    }

    public static int findAnswerByDP(){
        System.out.println("findAnswerByDP()");
        int answer = 0;
        int [] DP = new int[D + 1];
        int i, j;

        //D로 가는데 필요한 거리 초기화//<- 0가는데 필요한 거리 0 ~ D가는데 필요한 거리 D...
        for(i = 0; i <= D; i++){
            DP[i] = i;
        }

        System.out.print("최초 이동거리 : ");
        for(i = 1; i <= D; i++){
            System.out.print(DP[i] + " ");
        }

        System.out.print("\n짧은 이동거리 : ");
        for(i = 1; i <= D; i++){//현재 위치
            DP[i] = Math.min(DP[i], DP[i-1] + 1);//지름길을 거쳐와서 이동거리가 줄었는지 확인
            for(j = 0; j < N; j++){//현재 위치가 지름길 사용 직후 위치와 동일하다면?
                if(shortCut[j][1] == i){
                    DP[i] = Math.min(DP[i], DP[shortCut[j][0]] + shortCut[j][2]);//지름길을 탄게 그대로 온거보다 짧은지 판단
                }
            }
            System.out.print(DP[i] + " ");
        }
        System.out.println();
        answer = DP[D];

        return answer;
    }
}