
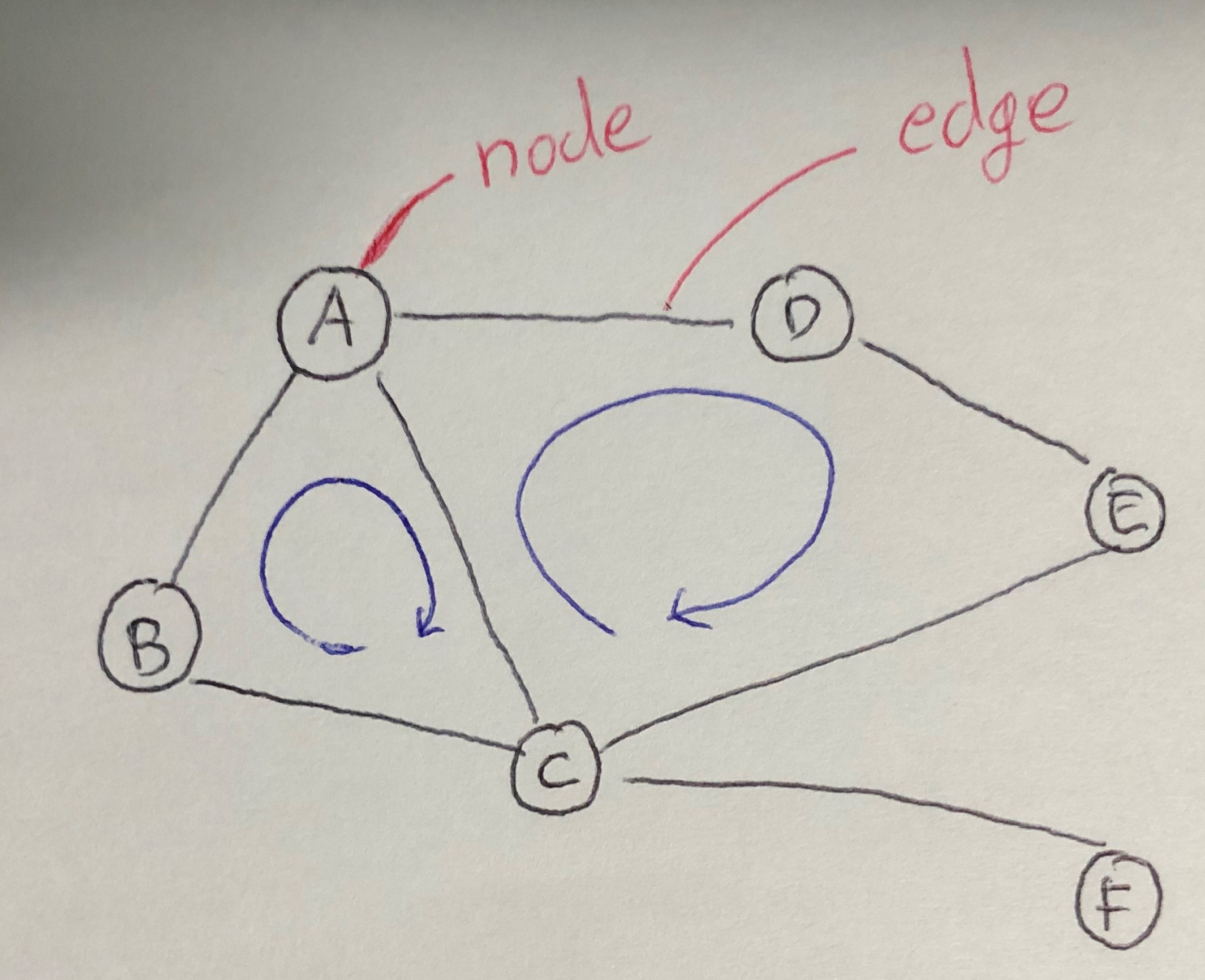
- 노드(node)를 간선(edge)으로 연결한 구조
1. 그래프의 기초
1.1 용어 정리
- node : 그래프의 정점.
A,B등 꼭지점을 말한다. - edge : node들을 이은 선을 말한다.
- degree : 무방향 그래프에서 하나의 정접에 인접한 정점의 수
- in-degree : 방향 그래프에서 한 노드로 들어오는 간선의 수(진입차수)
- out-degree : 방향 그래프에서 한 노드에서 나가는 간선의 수(진출차수)
1.2 특징
- 네트워크 모델이다.
- 출발 노드에서 도착 노드까지 여러 개의 경로를 가질 수 있다.
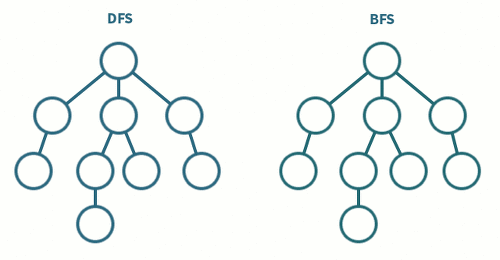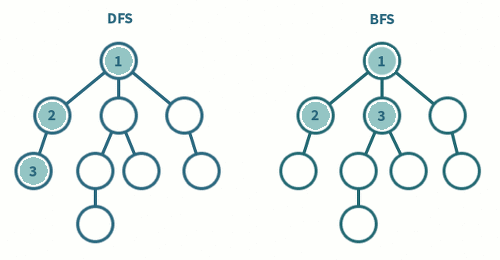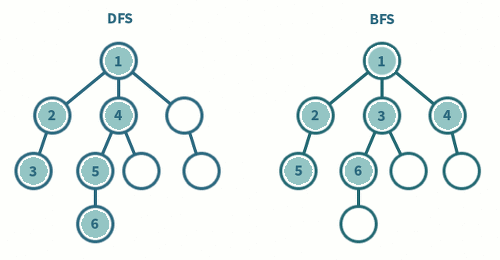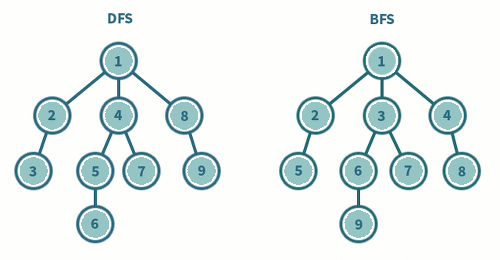
- 깊이 우선 탐색(DFS) / 너비 우선 탐색(BFS) 방법으로 순회할 수 있다.
- 루트(root)노드와 부모-자식 관계가 없다.
2. 그래프의 종류
2.1 무방향 그래프
- 간선을 통해서 양방향으로 이동이 가능한 그래프
- A노드에서 B노드로 갈 수 있다면, B에서 A로도 갈 수 있다.
2.2 방향 그래프
- 무방향 그래프와 다르게 A노드에서 B노드로 갈 수 있어도, 반대로는 불가능할 수 있다.
2.3 가중치 그래프
- 간선에 비용이나 가중치가 있는 그래프
- 네트워크 구조라고도 한다.
3. 그래프의 구현

3.1 인접 리스트로 구현하기
- 모든 노드의 간선 정보를 리스트에 저장하는 방법
- 필요한 만큼의 정보만 저장하여 공간 활용의 효율이 좋지만, 연결 정보를 확인하는데 시간이 걸린다.
- 그래프가 적은 수의 노드와 간선으로 이루어져 있을 때 효과적이다.
N = 7
edge_data = [1, 2, 1, 5, 1, 3, 2, 6, 3, 4, 4, 5, 5, 7, 6, 7]
adjacency_list = [[] for _ in range(N+1)]
for i in range(0, len(edge_data), 2):
# 두 개의 노드 정보를 담는다.
node_num_1 = edge_data[i]
node_num_2 = edge_data[i+1]
# 무방향 그래프이므로 두 개의 정보를 저장한다.
adjacency_list[node_num_1].append(node_num_2)
adjacency_list[node_num_2].append(node_num_1)edge_data에는 간선의 정보가 담겨 있다. 맨 처음 두 개는 1번 노드에서 2번 노드로 이어진다는 의미이다. 무방향 그래프를 구현하고 있으므로 반대 방향으로도 이어진다는 정보를 추가해야 한다.
[[],
[2, 5, 3],
[1, 6],
[1, 4],
[3, 5],
[1, 4, 7],
[2, 7],
[5, 6]]
0번 노드는 존재하지 않지만 인덱스가 zero-based이기 때문에 편의상 위와 같이 구성했다.
인접행렬로 구현하기
- 이차원 배열을 이용해서 간선 정보를 저장하는 방법
- 이차원 배열을 0으로 초기화한 뒤, 연결된 부분을 1로 바꿔주는 방법을 사용할 수 있다.
- 배열을 이용하기 때문에 연결 정보를 확인하는데 시간이 비교적 적게 걸리지만, 불필요한 공간을 사용한다는 단점이 있다.
- 인접리스트와 반대로 노드와 간선 정보가 매우 많을 때 사용하면 효과적이다.
N = 7
edge_data = [1, 2, 1, 5, 1, 3, 2, 6, 3, 4, 4, 5, 5, 7, 6, 7]
adjacency_matrix = [[0] * (N + 1) for _ in range(N + 1)]
for i in range(0, len(edge_data), 2):
node_num_1 = edge_data[i]
node_num_2 = edge_data[i+1]
adjacency_matrix[node_num_1][node_num_2] = 1
adjacency_matrix[node_num_2][node_num_1] = 1이차원 배열을 사용한 것을 제외하곤, 인접리스트와 로직은 비슷하다.
[
[0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 1, 0, 1, 0, 0],
[0, 1, 0, 0, 0, 0, 1, 0],
[0, 1, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 1, 0, 0],
[0, 1, 0, 0, 1, 0, 0, 1],
[0, 0, 1, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 1, 1, 0]
]
이번에도 마찬가지로 편의상 (N+1)행, (N+1)열을 이용했다. 무방향 그래프이므로 대칭행렬을 이룬다.
4. 그래프의 순회
그래프는 보편적으로 깊이우선탐색과 너비우선탐색을 이용한다.

4.1 깊이우선탐색(DFS) 구현
스택 자료구조를 이용하면 깊이우선 탐색을 구현할 수 있다.
visited = [0] * (N + 1)
stack = []
def DFS(n):
stack.append(1)
while stack:
tmp = stack.pop()
if visited[tmp] == 0:
visited[tmp] = 1
print(tmp, end=" ")
for node in adjacency_list[tmp]:
stack.append(node)
return
- 1번부터 순회를 시작했으므로 stack에 1을 저장한다.
- stack에서 맨 뒤에 요소를 pop한 뒤 방문 여부를 확인한다.
- 방문하지 않았을 경우 방문 체크를 하고 해당 노드에서 접근 가능한 모든 노드를 stack에 저장한다.
- stack이 빌 때까지 반복하며 모든 노드를 방문했을 경우 종료된다.
인접리스트 방식을 사용해서 그래프 정보를 저장했다. visited 리스트의 역할은 방문했던 노드를 체크해서 다시 방문하는 것을 방지하는 것이다.
n은 순회를 시작할 노드의 번호이며, 필자는 1번에서 시작했다.
결과 : 1 3 4 5 7 6 2
4.2 너비우선탐색(DFS) 구현
큐 자료구조를 이용하면 깊이우선 탐색을 구현할 수 있다.
visited = [0] * (N + 1)
queue = []
def BFS(n):
queue.append(1)
while queue:
tmp = queue.pop(0)
if visited[tmp] == 0:
visited[tmp] = 1
print(tmp, end=" ")
for node in adjacency_list[tmp]:
queue.append(node)
return탐색할 노드를 저장할 자료구조가 스택이 아닌 큐를 사용하는 것을 제외하면 깊이우선탐색과 동일한 로직으로 작동한다.
결과 : 1 2 5 3 6 4 7


