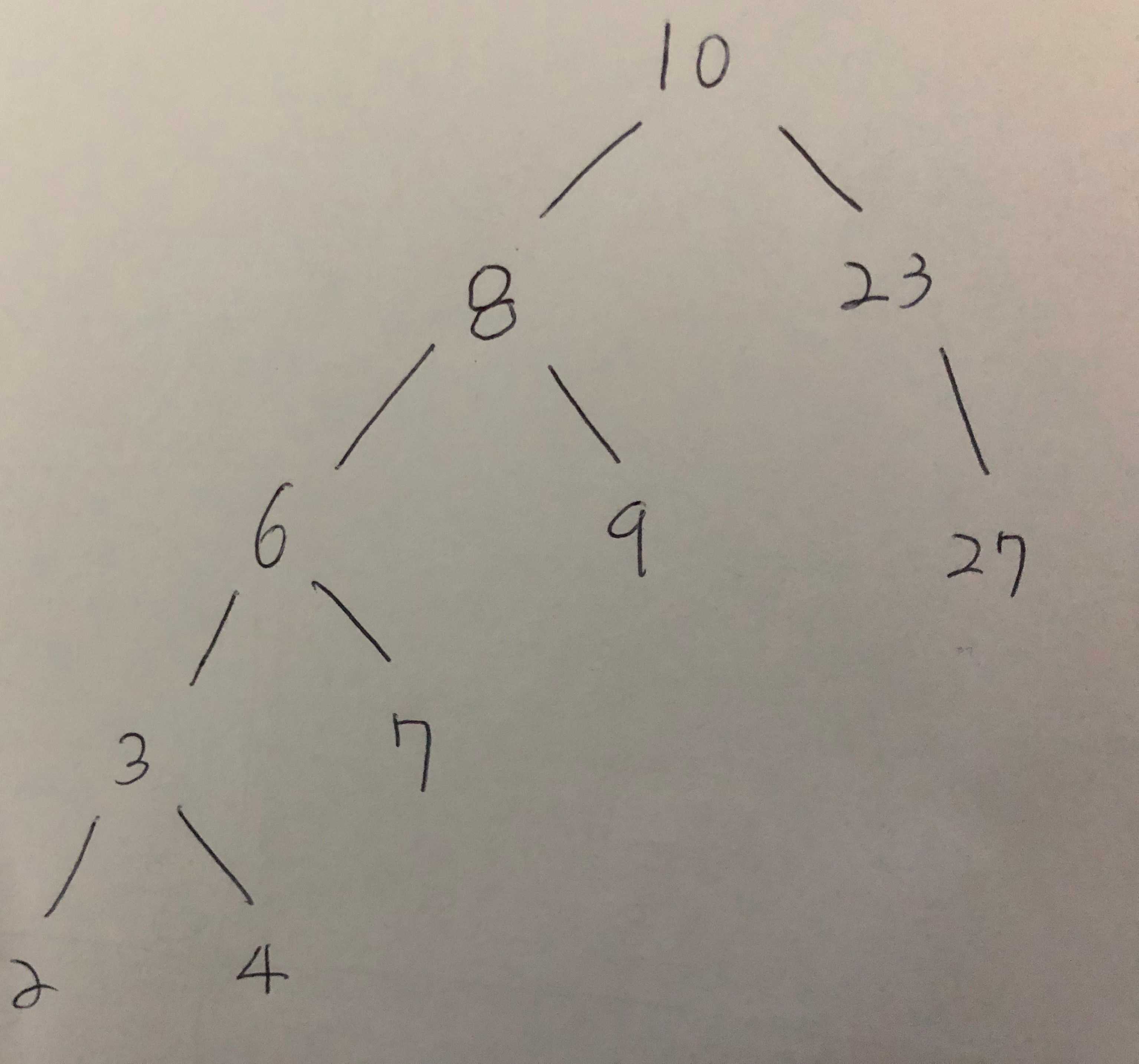
- 그래프 구조의 일종으로 볼 수 있다.
- 하나의 루트 노드를 갖는다.
- 모든 노드는 부모 노드와 0개 이상의 자식 노드를 갖는다.(루트 노드 제외)
- 임의의 두 노드간 경로는 단 하나만 존재하며, 사이클이 불가능하다.
- 전위 / 중위 / 후위 의 순회 방법이 있다.
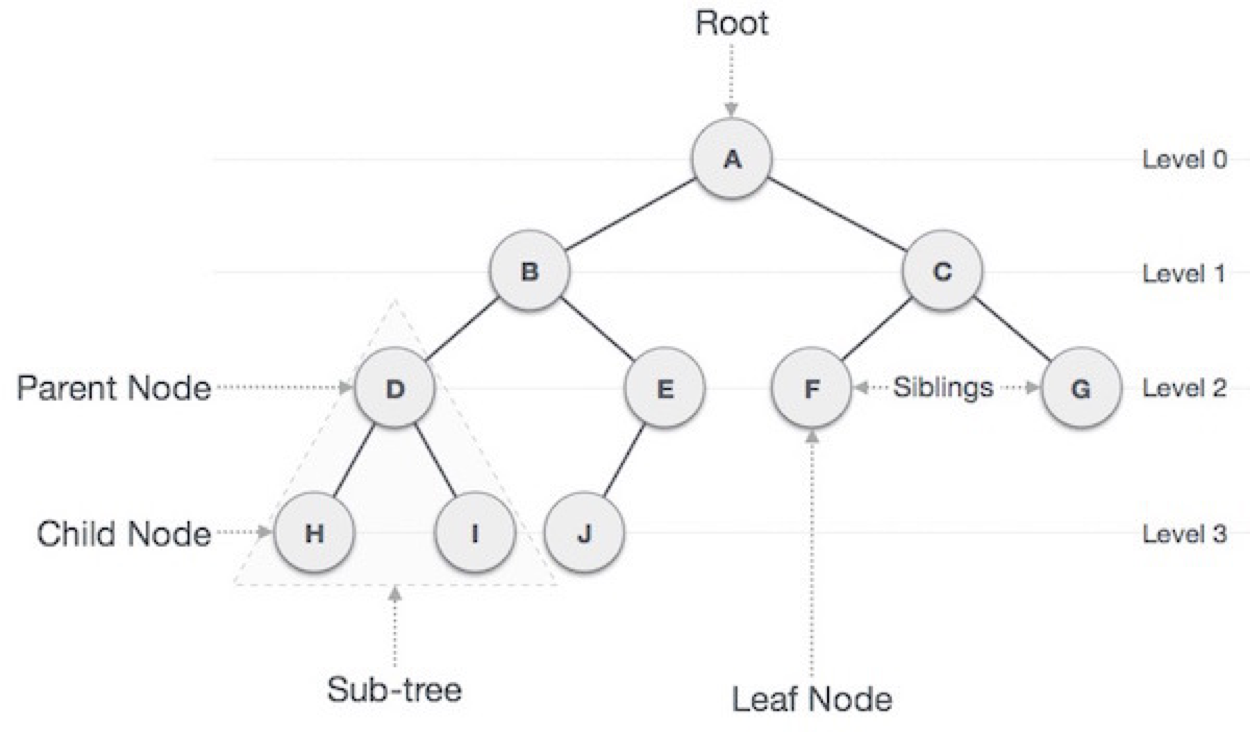
1. 트리 구조 용어 정리
- 루트 노드(Root Node) : 부모가 없는 최상위 노드. 하나만 존재
- 단말 노드(Leaf Node) : 자식이 없는 최하위 노드.
- 내부 노드(internal) : 루트 / 단말 노드가 아닌 노드
- 간선(Edge) : 노드를 연결하는 선
- 형제(Sibiling) : 같은 부모 노드를 공유하는 노드
- 노드의 크기 : 자신을 포함한 모든 자손 노드의 개수
- 노드의 깊이 : 어떤 노드에 도달하기 위한 간선의 수
- 노드의 레벨 : 트리의 특정 깊이를 가지는 노드의 집합
- 노드의 차수 : 노드가 가진 간선의 수
- 트리의 차수 : 트리의 최대 차수
- 트리의 높이 : 루트 노드로부터 가장 깊이 있는 노드의 깊이
트리도 많은 종류가 있지만, 이 포스트에서는 트리 구조 중에서도 많이 사용하는 이진 탐색 트리에 대한 종류와 추가, 순회(탐색), 삭제하는 방법을 정리하고 구현해 볼 것이다.
2. 이진 트리의 종류
완전 이진 트리
- 마지막 레벨을 제외하면 모든 레벨이 가득 차 있는 트리구조.
- 마지막 레벨도 왼쪽에서 오른쪽으로 채워져야 한다.
- 왼쪽에서부터 순차적으로 채워지기 때문에 배열을 이용하면 효율적으로 구현이 가능하다.
전 이진 트리
- 모든 노드가 0 또는 2개의 자식 노드를 가지는 트리 구조
포화 이진 트리
- 전 이진 트리와 완전 이진 트리의 특성을 모두 가지고 있는 트리 구조
- 모든 단말 노드는 같은 높이에 있어야 하며, 마지막 단계에서 노드의 수가 최대가 되어야 한다.
3. 이진 탐색 트리 구현
왼쪽의 자식노드는 부모보다 작으며, 오른쪽 자식 노드는 부모보다 큰 값을 가지도록 구성한 이진 트리이다.
3.1 배열로 구현하기
노드 삽입
tree = [None] * 20
tree[1] = 5
print(tree)
def add_node(num, index = 1):
while True:
if num <= tree[index]:
index = 2 * index
else:
index = 2 * index + 1
if tree[index] == None:
tree[index] = num
break
print(tree)노드의 인덱스를 구할 땐 다음과 같다.
- 노드 n의 부모 노드 = n/2
- 노드 n의 왼쪽 자식 = n*2
- 노드 n의 왼쪽 자식 = n*2 + 1
위의 규칙에 따라 노드의 인덱스를 구해서 값을 바꿔주면 된다.
노드 탐색
def find_node(num, index = 1):
while tree[index] != num:
if tree[index] != None:
if num <= tree[index]:
index = 2 * index
else:
index = 2 * index + 1
return index삽입과 마찬가지로 이진 탐색 트리의 규칙에 따라 노드를 탐색한 뒤 해당 노드가 있는 배열의 인덱스를 반환한다.
노드 삭제
이진 트리에서 노드를 삭제할 때는 세 가지 경우에 따라 다르게 진행한다.
- 단말 노드를 삭제할 때
- 자식 노드가 하나인 노드를 삭제할 때
- 자식 노드가 두 개인 노드를 삭제할 때
단말 노드를 삭제할 때는 해당 노드를 삭제하기만 하면 된다.
하나의 자식 노드를 가지고 있을 경우 해당 노드를 삭제하고 부모 노드와 자식 노드를 이어주면 된다.
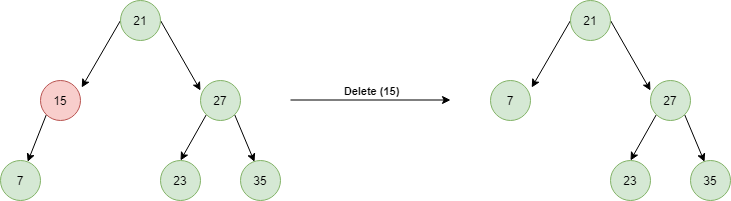두 개의 자식 노드를 가지고 있을 경우
- 왼쪽에서 가장 큰 값
- 오른쪽에서 가장 작은 값
위의 두 가지 중 하나의 값과 바꿔주면 된다. 위 두 가지 모두 반드시 단말 노드이기 때문에 값을 교환한 후 값이 바뀐 단말 노드를 삭제해주면 된다.
배열로 이진 탐색 트리를 만들면, 2번(하나의 자식 노드)의 경우 배열이라는 자료구조의 특성상 하나의 노드를 삭제하면 하위 노드들의 인덱스를 모두 재조정해주어야 한다. 그래서 두 개의 자식 노드를 가지고 있는 경우와 같은 방법으로 삭제를 구현했다.
def del_node(num):
index = find_node(num)
left = 2 * index
right = 2 * index + 1
# 단말 노드
if tree[left] == None and tree[right] == None:
tree[index] = None
# 자식 노드를 두 개 가진 노드
elif tree[left] != None and tree[right] != None:
while tree[2 * right] != None:
right = 2 * right
tree[index] = tree[right]
tree[right] = None
#자식 노드를 하나 가진 노드
else:
# 오른쪽 노드만 가졌을 때
if tree[left] == None:
while tree[2 * right] != None:
right = 2 * right
tree[index] = tree[right]
tree[right] = None
#왼쪽 노드만 가졌을 때
else:
while tree[2 * left + 1] != None:
left = 2 * left
tree[index] = tree[left]
tree[left] = None3.2 연결리스트로 구현
# 노드
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
# 이진 탐색 트리
# 노드
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
# 이진 탐색 트리
class BinaryTree:
def __init__(self, value):
new_node = Node(value)
self.root = new_node
def addNode(self, value):
new_node = Node(value)
tmp = self.root
while True:
# 현재 노드(tmp)보다 크고
if tmp.value > new_node.value:
# 왼쪽 노드가 비었다면 왼쪽 노드로
if tmp.left == None:
tmp.left = new_node
break
# 비어 있지 않다면 현재노드를 왼쪽 노드로 변경
else:
tmp = tmp.left
# 현재 노드(tmp)보다 작거나 같고
else:
# 오른쪽 노드가 비었다면 오른쪽 노드로
if tmp.right == None:
tmp.right = new_node
break
# 비어 있지 않다면 현재노드를 오른쪽 노드로 변경
else:
tmp = tmp.right
def findNode(self, value):
tmp = self.root
while tmp.value != value:
if tmp.value > value:
parant = tmp
tmp = tmp.left
else:
parant = tmp
tmp = tmp.right
if tmp == None:
break
if tmp.value == value:
return tmp, parant
return False, False
def deleteNode(self, value):
target, parant = self.findNode(value)
if not target:
print("해당 노드가 없습니다.")
# 삭제할 노드가 존재 한다면
else:
# 단말 노드일 경우
if target.left == None and target.right == None:
if parant.value > target.value:
parant.left = None
else:
parant.right = None
# 왼쪽 자식 노드만 가지고 있을 경우
elif target.left != None and target.right == None:
if parant.value > target.value:
parant.left = target.left
else:
parant.right = target.left
# 오른쪽 자식 노드만 가지고 있을 경우
elif target.left == None and target.right != None:
if parant.value > target.value:
parant.left = target.right
else:
parant.right = target.right
# 두 개의 자식 노드를 가지고 있을 경우
else:
tmp = target.left
# 단말 노드를 찾을 때까지
while tmp.right != None and tmp.left != None:
# 오른쪽 자식 노드로 이동
tmp = tmp.right
target_num = tmp.value # 왼쪽에서 가장 큰 값
self.deleteNode(target_num) # 왼쪽에서 가장 큰 값 삭제
target.value = target_num # 삭제하려고 한 노드 value 변경아래와 같이 임의의 이진 탐색 트리를 만들었다.
tree = BinaryTree(10)
tree.addNode(8)
tree.addNode(23)
tree.addNode(9)
tree.addNode(6)
tree.addNode(7)
tree.addNode(3)
tree.addNode(2)
tree.addNode(4)
tree.addNode(27)
이진 탐색 트리에서 삭제 연산을 할 때, 고려해야 하는 부분이 또 있다. 두 개의 자식 노드를 가지고 있는 노드를 삭제할 땐
- 왼쪽에서 가장 큰 값
- 오른쪽에서 가장 작은 값
위의 두 가지 중 하나를 택해서 삭제하고자 하는 노드(A)와 값을 바꾸기 위해 택한 노드(B)를 삭제한다.
그런데 (B)노드가 단말 노드가 아닐 수도 있다. 예를 들면 왼쪽에서 가장 큰 값을 가지는 노드가 왼쪽 자식 노드 하나만 가지고 있는 경우가 있다.
그래서 구현할 때 (B)노드의 value를 따로 저장한 뒤에 해당 노드를 재귀 방식으로 삭제 연산을 한 번 더 진행한다.
이 때, (B)노드는 절대로 자식 노드를 두 개 가질 수 없다. 자식 노드를 두 개 가지고 있으면 값을 바꾸기 위해 택하지 않는다.
3.3 이진 트리 순회
def Traversal(self, order, tmp):
if order == 'pre':
print(tmp.value, end=" ")
if tmp.left != None:
self.Traversal(order, tmp.left)
if tmp.right != None:
self.Traversal(order, tmp.right)
elif order == 'in':
if tmp.left != None:
self.Traversal(order, tmp.left)
print(tmp.value, end=" ")
if tmp.right != None:
self.Traversal(order, tmp.right)
elif order == 'post':
if tmp.left != None:
self.Traversal(order, tmp.left)
if tmp.right != None:
self.Traversal(order, tmp.right)
print(tmp.value, end=" ")
