
이 글의 목적?
하노이 탑 문제는 재귀에서 유명한 문제라고 한다. 이 유명한 것을 나는 이해가 안가 몇날 몇일을 고민했다. 물론 인터넷에서 돌아다니는 풀이도 살펴보았지만, 이해하기 쉽지는 않았다. (여러 레퍼런스들 중에서 가장 이해가 되었던 두 레퍼런스를 첨부해놓았다!)
결론적으로는 잘 해결했지만, 완벽하다고는 할 수 없다. 하지만 여기서 더 머물다가는 다른 문제들을 풀을 수 없으니, 어느 정도 수준까지만 이해도를 올리고 넘어가는게 좋을 것 같다.
문제
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.
- 한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
- 쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.
- 이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.
아래 그림은 원판이 5개인 경우의 예시이다.

풀이
솔직히 말하자면 이미지를 보면서 문제를 읽고 이해하기 어려웠다. 과정에 대한 설명없이 그저 1번 장대에서 3번 장대로 옮겼다! 라는 정보만 보여주다보니 불친절하다고 생각했다.
과정에 대한 움직임을 확인하기 위해 내가 참고한 레퍼런스에서의 이미지를 가져와보았다. (이 얼마나 친절한가! 👍)
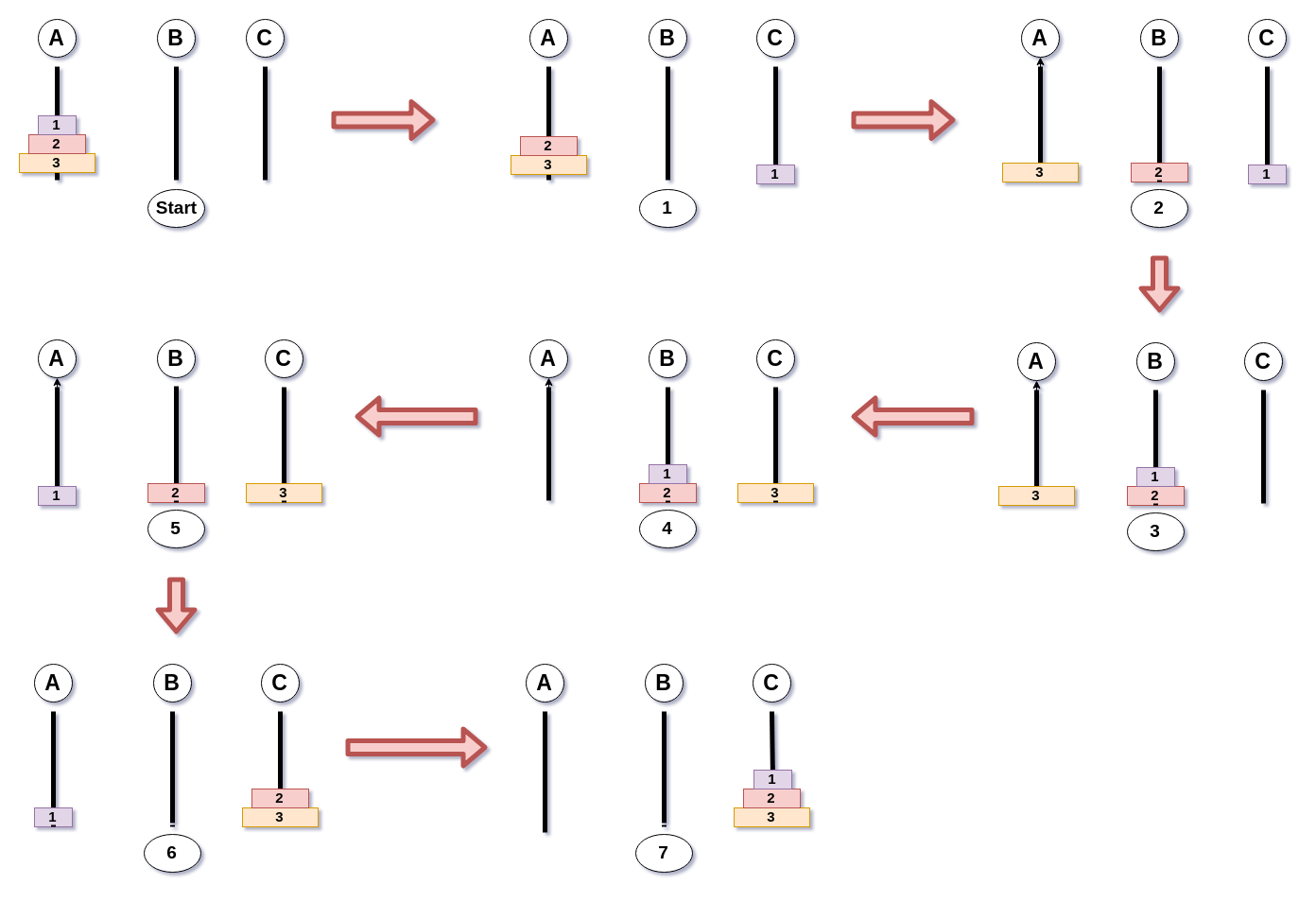
카테고리 자체가 재귀라는 점에서 재귀적으로 문제를 풀어야한다는 것을 알고는 있었지만, 아무리 생각해도 위의 과정에서 어떤 부분이 반복적으로 진행되는지, 어떤 규칙을 가지고 있는지 찾기 어려웠다.
그래서 여러 풀이 글들을 읽고 공통적으로 발견할 수 있었던 것은 바로 "n개의 원판이 있고 이를 목표 장대에 옮기고자 할 때 n-1개의 원판은 보조 장대에 옮겨야 한다!" 라는 점이다.
중요한 부분임을 알고는 있었지만, 도저히 설계를 어떻게 해야할지 생각이 나지 않다보니 과정을 보여주며 간략하게 코드로 옮겨보는 유튜브 영상을 보니 조금씩 이해되기 시작했다.
유튜브 영상의 내용을 가져와서 하나씩 정리해가며 다시 이해해보자.
재귀 함수를 위한 기본 아이디어는 이렇다.
hanoi(5개의 원판을, 1번 장대에서, 3번 장대로, 2번 장대를 보조로 사용)

그럼 가장 최소의 원판을 가질 경우에는 어떻게 해야할까? 이미지에서도 볼 수 있듯, 원판이 1개일 때는 3번 장대로 한번에 옮길 수 있다.
hanoi(1개의 원판을, 1번 장대에서, 3번 장대로, 2번 장대를 보조로 사용)
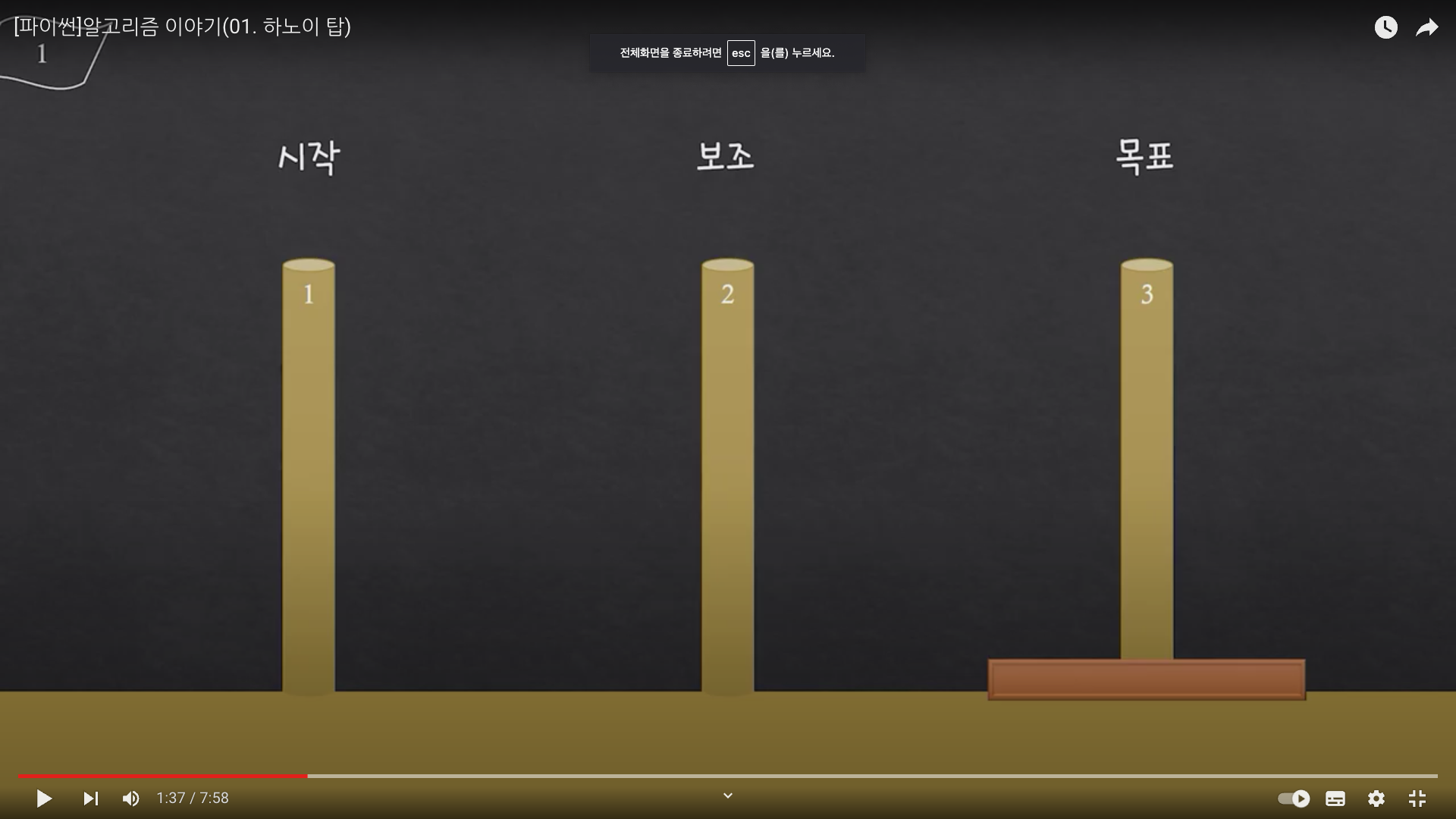
그럼 두 개일 때를 가정해보자.
원래라면 두 개의 원판을 3번 장대로 옮기는 것이 목표이므로 다음과 같은 함수가 호출될 것이다.
hanoi(2개의 원판을, 1번 장대에서, 3번 장대로, 2번 장대를 보조로 사용)
그럼 각 원판을 옮기는 과정은 어떻게 될까?
hanoi(1개의 원판을, 1번 장대에서, 2번 장대로, 3번 장대를 보조로 사용)
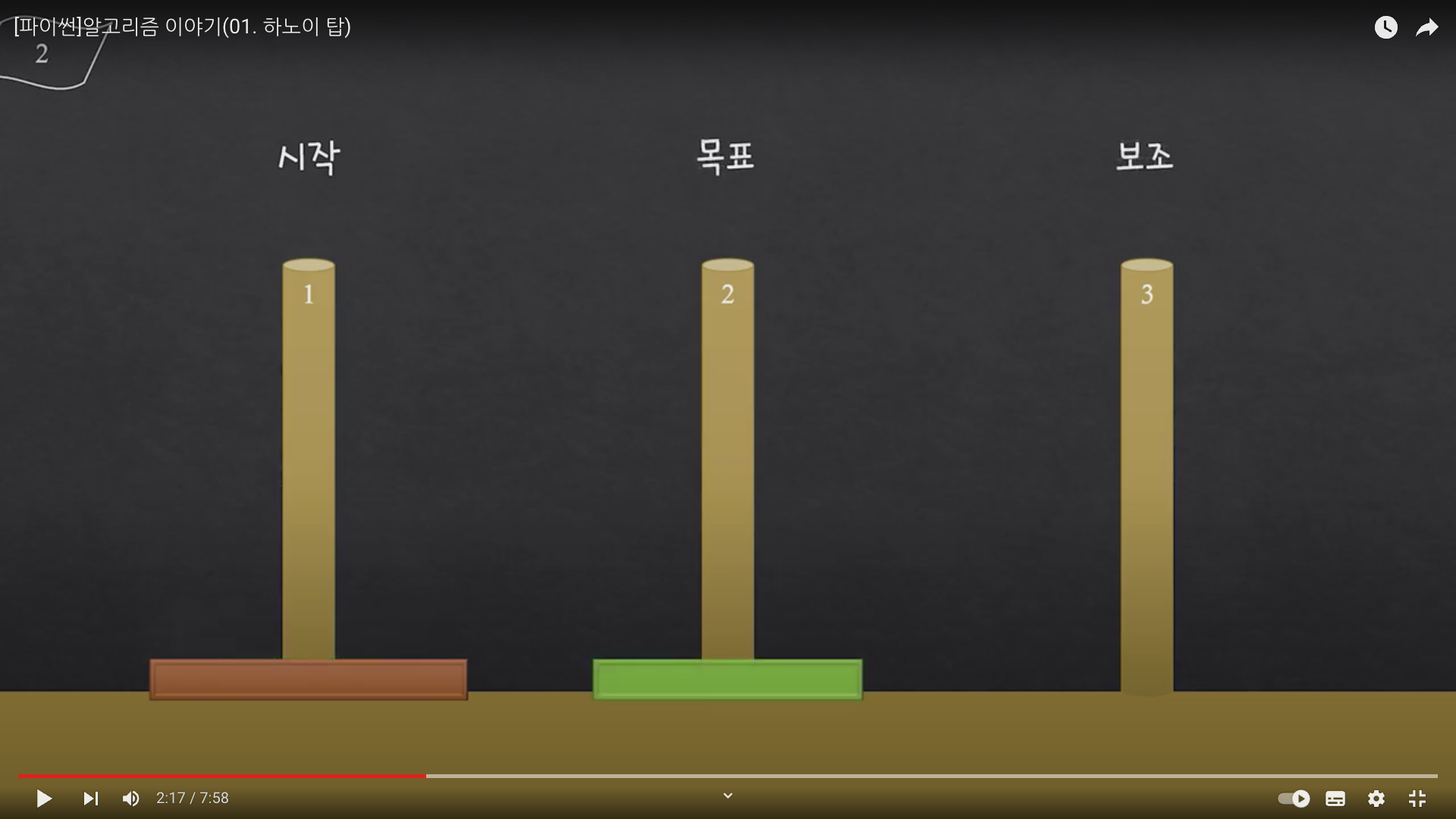
hanoi(1개의 원판을, 1번 장대에서, 3번 장대로, 2번 장대를 보조로 사용)
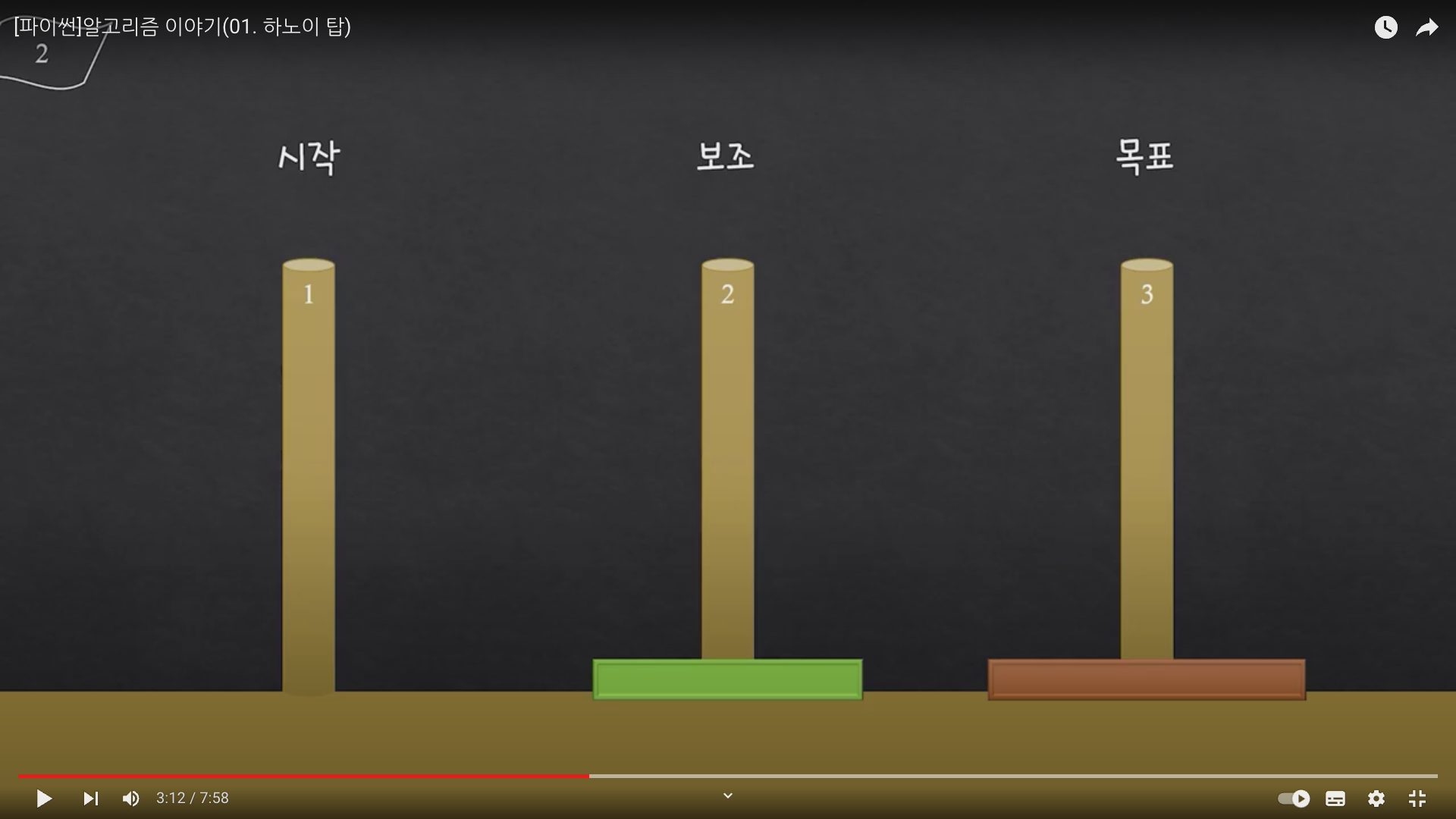
hanoi(1개의 원판을, 2번 장대에서, 3번 장대로, 1번 장대를 보조로 사용)
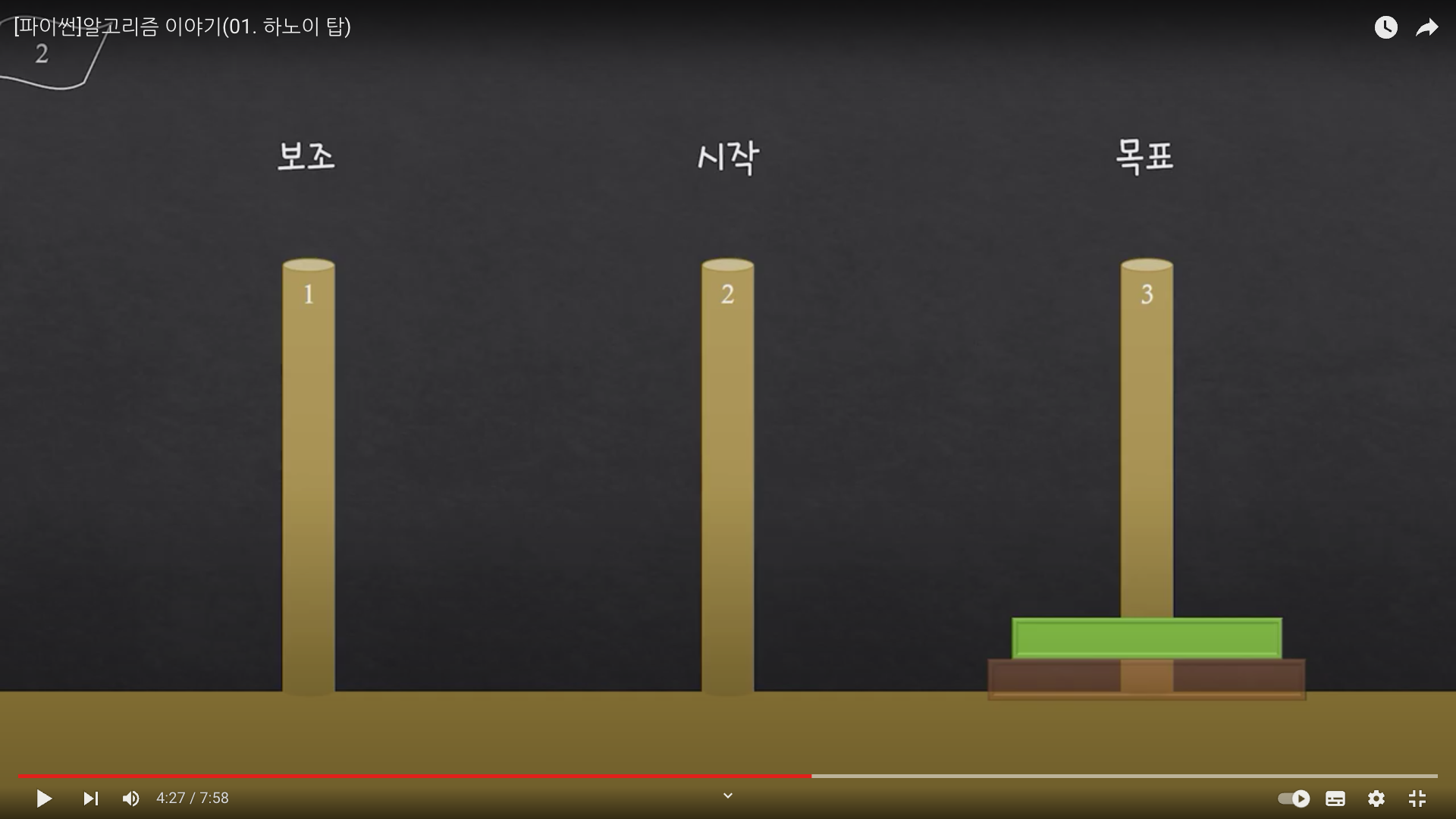
대충 보면 뭔가 보일 듯 하다.. 여기서 또 확인할 수 있는 부분으로는, 마지막에 보조 장대에 있는 원판을 목표 장대로 옮긴다는 과정이 필수적으로 들어가는 것 이다. 그럼 원판이 세 개일 때를 생각해보자. (이번에는 그림 없이!)
hanoi(3, 1, 3, 2) : 3개의 원판을 1번 장대에서 3번 장대로 2번 장대를 보조로 사용
hanoi(2, 1, 2, 3) : 2개의 원판을 1번 장대에서 2번 장대로 3번 장대를 보조로 사용
hanoi(1, 1, 3, 2) : 1개의 원판을 1번 장대에서 3번 장대로 2번 장대를 보조로 사용
✋🏻 원판이 1개이고 이를 이동시켰으니 더 이상할 일이 없음!
hanoi(1, 3, 2, 1) : 1개의 원판을 3번 장대에서 2번 장대로 1번 장대를 보조로 사용
✋🏻 원판이 1개이고 이를 이동시켰으니 더 이상할 일이 없음!
hanoi(2, 2, 3, 1) : 2개의 원판을 2번 장대에서 3번 장대로 1번 장대를 보조로 사용
hanoi(1, 2, 1, 3) : 1개의 원판을 2번 장대에서 1번 장대로 3번 장대를 보조로 사용
✋🏻 원판이 1개이고 이를 이동시켰으니 더 이상할 일이 없음!
hanoi(1, 1, 3, 2) : 1개의 원판을 1번 장대에서 3번 장대로 2번 장대를 보조로 사용
✋🏻 원판이 1개이고 이를 이동시켰으니 더 이상할 일이 없음!즉, 아이디어는 "n개의 원판이 있고 목표 장대로 옮기고자 할 때 n-1개의 원판은 보조 장대에 있어야하고, 마지막 과정에서 n-1개의 원판은 다시 목표 장대로 옮겨야 마무리가 된다." 라는 것이다.
코드
이를 바탕으로 코드를 작성하면 다음과 같다.
import java.util.Scanner;
public class Main {
public static final Scanner scanner = new Scanner(System.in);
public static int k; // 이동 횟수
public static StringBuilder sb = new StringBuilder();
public static void hanoi(int n, String start, String to, String assist) {
if(n == 1) {
k++;
sb.append(start).append(" ").append(to).append("\n");
return;
}
hanoi(n-1, start, assist, to);
sb.append(start).append(" ").append(to).append("\n");
hanoi(n-1, assist, to, start);
k++;
}
public static void main(String[] args) {
int n = scanner.nextInt();
// n개의 원판을 1번 장대에서 3번 장대로 이동시키고 2번 장대를 보조로 사용
hanoi(n, "1", "3", "2");
System.out.println(k);;
System.out.println(sb);
scanner.close();
}
}