
이 글의 목적?
에라토스테네스의 체를 이용하여 소수를 구하는 문제를 풀며 멘붕이 온 상태에 이어서 별 찍기 문제를 풀어보았는데 정말 헛웃음만 나왔다. 풀 수 있을 것 같은 자만심 때문도 있지만, 풀이를 보고도 제대로 이해하지 못해 많은 시간을 소비했다. (그럼에도 정답 비율이 53.435%라니...)
문제
재귀적인 패턴으로 별을 찍어 보자. N이 3의 거듭제곱(3, 9, 27, ...)이라고 할 때, 크기 N의 패턴은 N×N 정사각형 모양이다.
크기 3의 패턴은 가운데에 공백이 있고, 가운데를 제외한 모든 칸에 별이 하나씩 있는 패턴이다.
***
* *
***N이 3보다 클 경우, 크기 N의 패턴은 공백으로 채워진 가운데의 (N/3)×(N/3) 정사각형을 크기 N/3의 패턴으로 둘러싼 형태이다. 예를 들어 크기 27의 패턴은 예제 출력 1과 같다.
풀이
내가 먼저 접근한 방법을 먼저 이야기해보자. 나는 입력받은 n에 대하여 2차원 배열을 만들어주고 빈 공간을 만들어주는 방법으로 진행했다. 그리고 각 구멍을 만들어주는 부분에서 규칙을 찾고자 했다. 즉, 별로 모두 채워주고 삭제하는 방법을 생각해냈다.
그래서 가장 먼저 n이 27일 때만을 고려하여 별을 찍어보면서 규칙을 찾아보고자 했다. 하단의 코드는 각 빈 공간을 차례대로 순서를 매겨 이중 포문으로 작성해보았다.
import java.util.Scanner;
public class Main {
public static void main(String[] args {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
boolean[][] isBlank = new boolean[n][n];
// 가장 작은 구멍들
for (int i = 1; i < n; i+=3) {
for (int j = 1; j < n; j+=3) {
isBlank[i][j] = true;
}
}
// 1번째 구멍
for (int i = 3; i < 6; i++) {
for (int j = 3; j < 6; j++) {
isBlank[i][j] = true;
}
}
// 2번째 구멍
for (int i = 3; i < 6; i++) {
for (int j = 12; j < 15; j++) {
isBlank[i][j] = true;
}
}
// 3번째 구멍
for (int i = 3; i < 6; i++) {
for (int j = 21; j < 24; j++) {
isBlank[i][j] = true;
}
}
// 4번째 구멍
for (int i = 12; i < 15; i++) {
for (int j = 3; j < 6; j++) {
isBlank[i][j] = true;
}
}
// 5번째 구멍
for (int i = 12; i < 15; i++) {
for (int j = 12; j < 15; j++) {
isBlank[i][j] = true;
}
}
// 6번째 구멍
for (int i = 12; i < 15; i++) {
for (int j = 21; j < 24; j++) {
isBlank[i][j] = true;
}
}
// 7번째 구멍
for (int i = 21; i < 24; i++) {
for (int j = 3; j < 6; j++) {
isBlank[i][j] = true;
}
}
// 8번째 구멍
for (int i = 21; i < 24; i++) {
for (int j = 12; j < 15; j++) {
isBlank[i][j] = true;
}
}
// 9번째 구멍
for (int i = 21; i < 24; i++) {
for (int j = 21; j < 24; j++) {
isBlank[i][j] = true;
}
}
// 가장 큰 공간
for (int i = 9; i < 18; i++) {
for (int j = 9; j < 18; j++) {
isBlank[i][j] = true;
}
}
// 1, 2, 3 구멍 규칙
// (3) <= i < (6)
// (3 + 9k) <= j < (6 + 9k) (단, k는 0부터 시작)
// 4, 5, 6 구멍 규칙
// (12) <= i < (15)
// (3 + 9k) <= j < (6 + 9k) (단, k는 0부터 시작)
// 7, 8, 9 구멍 규칙
// (21) <= i < (24)
// (3 + 9k) <= j < (6 + 9k) (단, k는 0부터 시작)
// 가장 큰 구멍 규칙
// (9) <= i < 18
// (9) <= j < 18
// for (int i = n / 3; i < n / 3 * 2; i++) {
// for (int j = n / 3; j < n / 3 * 2; j++) {
// isBlank[i][j] = true;
// }
// }
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
System.out.print(isBlank[i][j] ? " " : 0 + "");
}
System.out.println();
}
scanner.close();
}
}여기서 규칙적인 부분은 가장 작은 구멍과 가장 큰 구멍을 제외한 곳에서 발견할 수 있었다. 이 규칙들을 바탕으로 구현한 코드는 다음과 같다.
import java.util.Scanner;
public class Main {
public static int n;
public static boolean[][] isBlank;
public static void recursion(int i) {
if(i <= 0) return;
int k = 0;
while(9 * k < n) {
for(int x = i - 3; x < i; x++ ) {
for(int y = 3 + 9 * k; y < 6 + 9 * k; y++) {
isBlank[x][y] = true;
}
}
k++;
}
recursion(i - 9);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
isBlank = new boolean[n][n];
// 가장 작은 구멍들
for (int i = 1; i < n; i+=3) {
for (int j = 1; j < n; j+=3) {
isBlank[i][j] = true;
}
}
recursion(n - 3);
// 가장 큰 공간
for (int i = n / 3; i < n / 3 * 2; i++) {
for (int j = n / 3; j < n / 3 * 2; j++) {
isBlank[i][j] = true;
}
}
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
System.out.print(isBlank[i][j] ? " " : "*" + "");
}
System.out.println();
}
scanner.close();
}
}구현한 코드가 잘 동작하는 것을 보면 나의 접근법은 틀리지 않았다고 생각한다. 다만 시간 초과라는 문제가 발생했기에 다른 방법을 찾아야했다. 내가 참고한 레퍼런스의 풀이를 이해해보자.
레퍼런스에서는 나와 동일하게 이차원 배열을 활용했다.
- n = 3

- n = 9

- n = 27
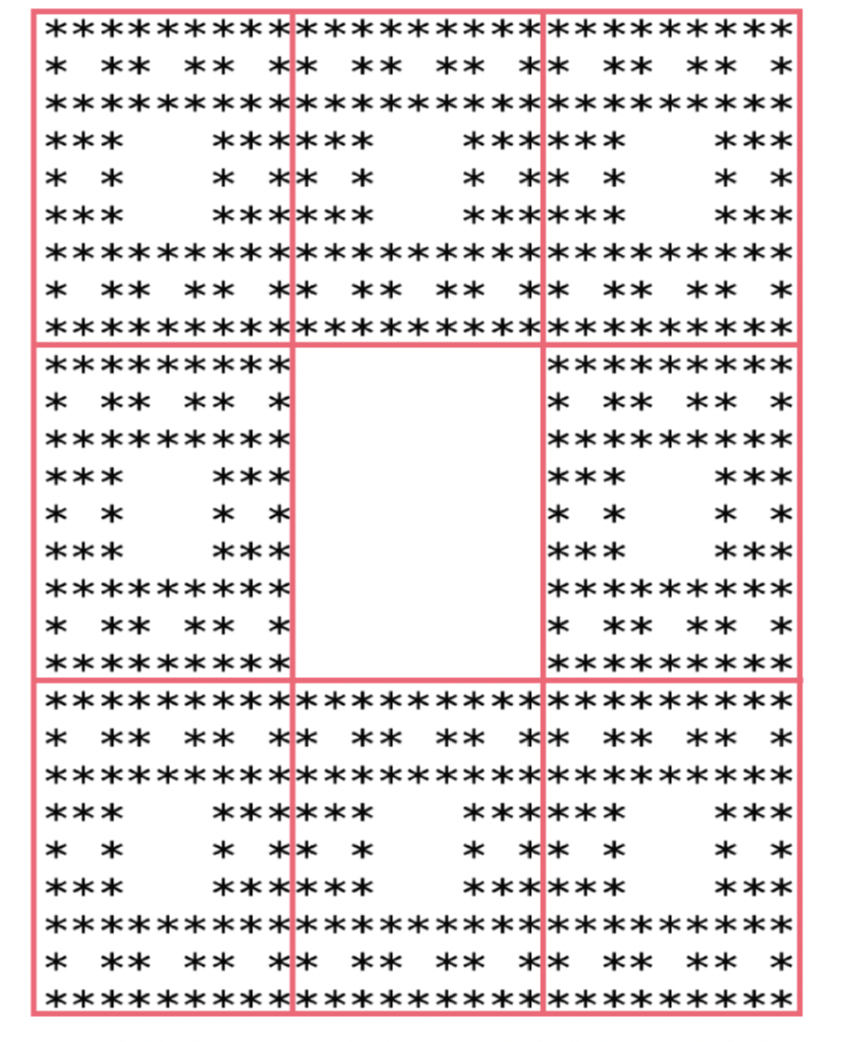
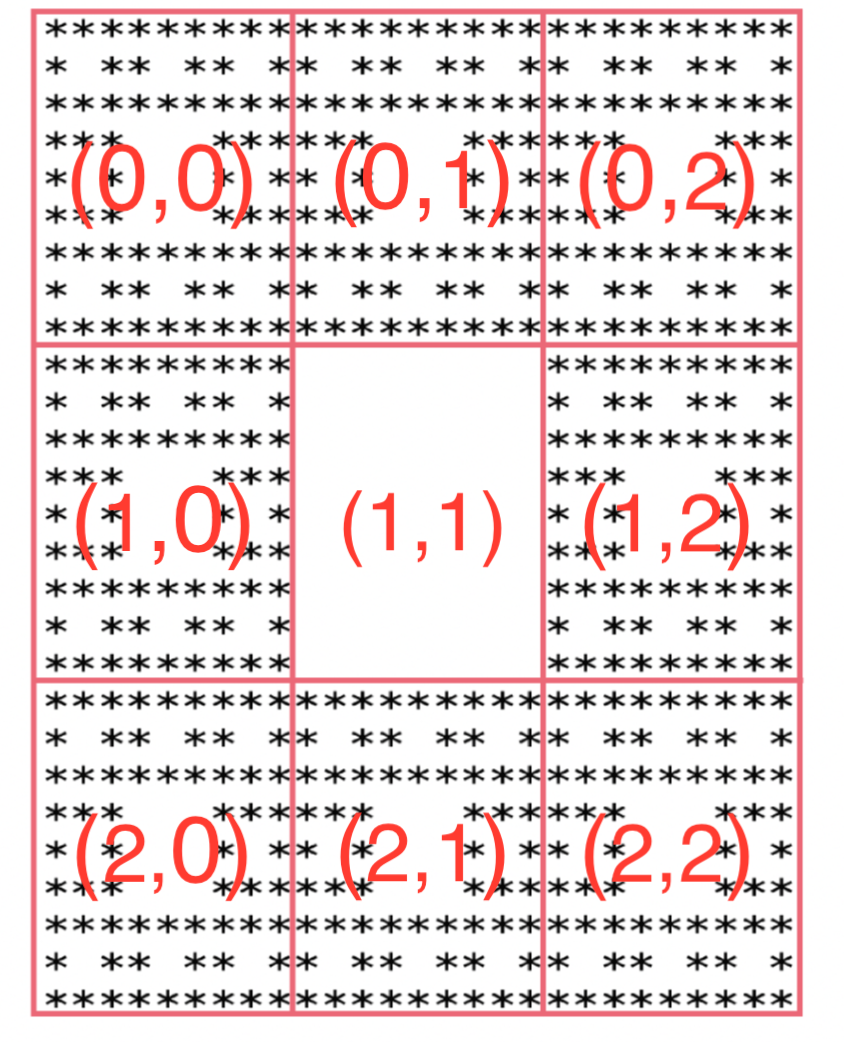
이미지처럼 빨간 경계선을 통해 각 케이스별로 찾을 수 있는 것은 9등분이되고, 9개의 블럭 중 가운데 블럭만이 비어있다는 것을 알 수 있다. 그리고 이를 이차원 배열로 표현하자면 arr[1][1] = (비어있음)이 되겠다.
이 방식으로 레퍼런스에서는 다음과 같은 트리 구조로 표현해놓았다.
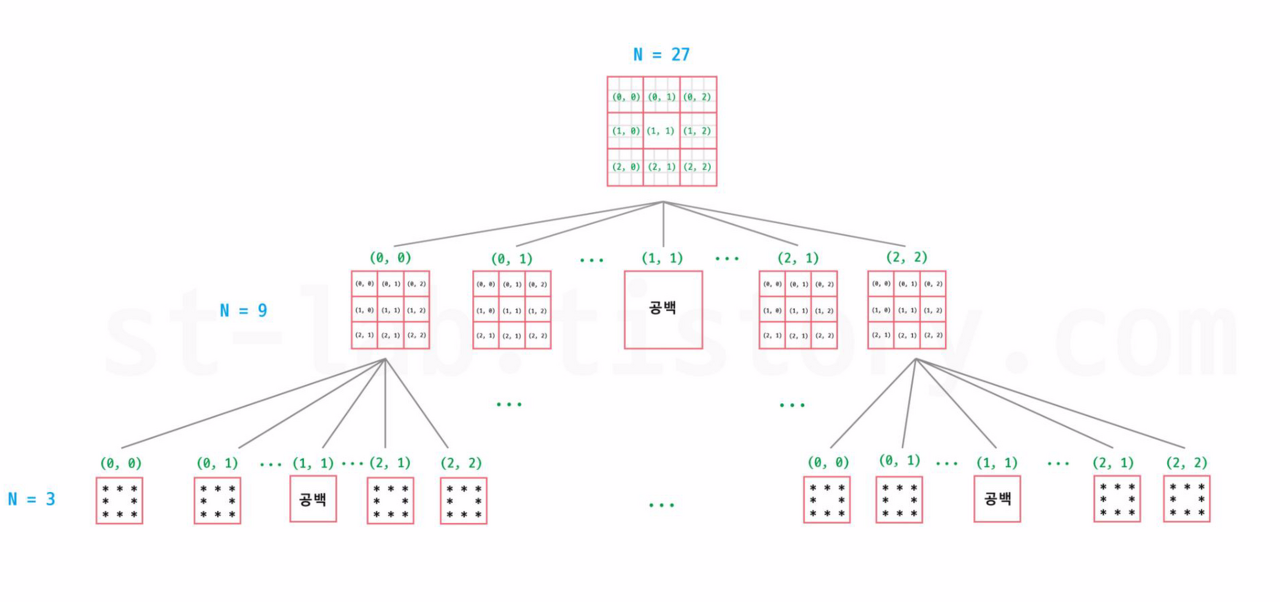
결국, 9등분으로 나누고 나뉜 블럭들의 좌표에 따라 재귀 호출을 하여 나눌 칸이 없을 때까지 반복하는 것이 레퍼런스의 풀이다.
코드
레퍼런스의 풀이에 따라 작성한 코드는 다음과 같다.
import java.util.Scanner;
public class Main {
public static char[][] arr;
public static void fillStar(int x, int y, int n, boolean isBlank) {
// 공백일 경우
if(isBlank) {
for(int i = x; i < x + n; i++) {
for(int j = y; j < y + n; j++) {
arr[x][y] = 32;
}
}
return;
}
// 더 이상 쪼갤 수 없는 블럭일 경우
if(n == 1) {
arr[x][y] = '*';
return;
}
// n = 27 일 경우, 한 블록의 사이즈는 9
// n = 9 일 경우, 한 블록의 사이즈는 3
// n 일 경우, 한 블록의 사이즈는 n / 3
int size = n / 3;
// 9등분된 상태에서 (1,1) 까지의 블록 수는 (0,0), (0,1), (0,2), (1,0) 총 4개
// 즉, 5번째 블록일 때는 가운데 가장 큰 비어있는 공간을 의미
int count = 0;
for(int i = x; i < x + n; i+=size) {
for(int j = y; j < y + n; j+=size) {
count++;
// (1,1)인 경우
if(count == 5) {
fillStar(i, j, size, true);
} else {
fillStar(i, j, size, false);
}
}
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
arr = new char[n][n];
// '*' 모두 채우기
fillStar(0, 0, n, false);
StringBuilder sb = new StringBuilder();
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
if (arr[i][j] == 0) {
sb.append(" ");
continue;
}
sb.append(arr[i][j]);
}
sb.append("\n");
}
System.out.println(sb);
scanner.close();
}
}