문제
https://www.acmicpc.net/problem/14500
폴리오미노란 크기가 1×1인 정사각형을 여러 개 이어서 붙인 도형이며, 다음과 같은 조건을 만족해야 한다.
- 정사각형은 서로 겹치면 안 된다.
- 도형은 모두 연결되어 있어야 한다.
- 정사각형의 변끼리 연결되어 있어야 한다. 즉, 꼭짓점과 꼭짓점만 맞닿아 있으면 안 된다.
정사각형 4개를 이어 붙인 폴리오미노는 테트로미노라고 하며, 다음과 같은 5가지가 있다.
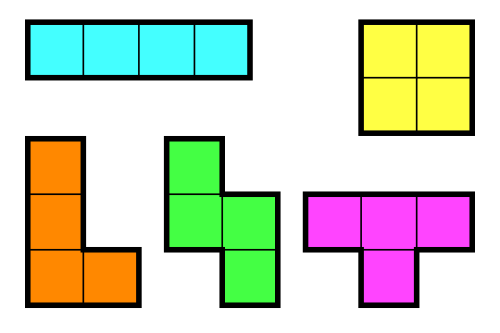
아름이는 크기가 N×M인 종이 위에 테트로미노 하나를 놓으려고 한다. 종이는 1×1 크기의 칸으로 나누어져 있으며, 각각의 칸에는 정수가 하나 쓰여 있다.
테트로미노 하나를 적절히 놓아서 테트로미노가 놓인 칸에 쓰여 있는 수들의 합을 최대로 하는 프로그램을 작성하시오.
테트로미노는 반드시 한 정사각형이 정확히 하나의 칸을 포함하도록 놓아야 하며, 회전이나 대칭을 시켜도 된다.
입력
첫째 줄에 종이의 세로 크기 N과 가로 크기 M이 주어진다. (4 ≤ N, M ≤ 500)
둘째 줄부터 N개의 줄에 종이에 쓰여 있는 수가 주어진다. i번째 줄의 j번째 수는 위에서부터 i번째 칸, 왼쪽에서부터 j번째 칸에 쓰여 있는 수이다. 입력으로 주어지는 수는 1,000을 넘지 않는 자연수이다.
출력
첫째 줄에 테트로미노가 놓인 칸에 쓰인 수들의 합의 최댓값을 출력한다.
예제 입력 1
5 5
1 2 3 4 5
5 4 3 2 1
2 3 4 5 6
6 5 4 3 2
1 2 1 2 1
예제 출력 1
19
예제 입력 2
4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
예제 출력 2
20
예제 입력 3
4 10
1 2 1 2 1 2 1 2 1 2
2 1 2 1 2 1 2 1 2 1
1 2 1 2 1 2 1 2 1 2
2 1 2 1 2 1 2 1 2 1
예제 출력 3
7
접근
처음에는 완전 탐색을 안 해보려고 우선순위 큐를 썼다.
가장 큰 숫자가 있는 칸의 위치 정보를 우선적으로 꺼내는 우선순위 큐를 선언하고,
현재까지 선택된 칸과 인접해 있고 아직 방문하지 않은 칸들의 위치 정보를 우선순위 큐에 넣었다.
그 상태에서 우선순위 큐에서 꺼낸 칸이 인접 칸 중에서 가장 숫자가 큰 칸이기 때문에, 그 칸을 선택하면 최적일 거라고 생각했다.
난 이렇게 하면 완전 탐색보다 빠를 줄 알았는데, 오히려 시간 초과가 났다.
1. 우선순위 큐에 대해 반복적으로 이뤄지는 정렬, poll, offer 연산으로 인한 오버헤드.
2. 완전 탐색을 하면 탐색 방향과 순서가 일관되게 정해지는 반면, 우선순위 큐를 사용해 탐색하면 탐색 방향이 중구난방이 됨. 그래서 DFS를 사용해 완전 탐색을 하면 딱 4칸만 방문하고 바로 종료되는 반면, 우선순위 큐를 사용해 탐색하면 선택된 칸과 인접해 있는 모든 칸을 방문하게 됨.
위 두 개가 가장 큰 이유인 것 같다.
한 방향만을 일관적으로 따라가다가, 범위를 벗어나거나 이미 방문한 칸이면 바로 백트래킹을 하는 게 오히려 낭비가 덜해서 빠른 것...
그리고 챗지피티 말로는 이런 방식은 최적해를 보장하지 않는다고 한다.
왜인지는 잘 모르겠다.....
무튼 간에 이 문제는 그냥 백트래킹하며 푸는 브루트 포스 문제였다. 그냥 하면 되는 거였는데 괜히 어렵게 생각했더니 오히려 오래 걸렸다...
ㅗ, ㅓ, ㅏ, ㅜ는 다른 테트로미노 모양과는 달리 가지가 두 갈래로 뻗어 나가야 하기에 백트래킹으로는 탐색이 불가능했고, 이 경우는 따로 처리를 해주었다.
구현
import java.io.*;
import java.util.*;
class Main {
static int result = 0;
static int n;
static int m;
static int[][] arr;
static boolean[][] visited;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
arr = new int[n][m];
visited = new boolean[n][m];
for (int i = 0; i < n; i++) {
String[] input = br.readLine().split(" ");
for (int j = 0; j < m; j++) {
arr[i][j] = Integer.parseInt(input[j]);
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
result = Math.max(result, putExclusiveTetromino(i, j));
visited[i][j] = true;
putTetromino(i, j, 1, arr[i][j]);
visited[i][j] = false;
}
}
System.out.println(result);
}
private static void putTetromino(int row, int col, int count, int sum) {
if (count == 4) {
result = Math.max(result, sum);
return;
}
int[] dx = {-1, 0, 1, 0};
int[] dy = {0, 1, 0, -1};
for (int i = 0; i < 4; i++) {
int nextX = row + dx[i];
int nextY = col + dy[i];
if (nextX >= 0 && nextX < n && nextY >= 0 && nextY < m && !visited[nextX][nextY]) {
visited[nextX][nextY] = true;
putTetromino(nextX, nextY, count + 1, sum + arr[nextX][nextY]);
visited[nextX][nextY] = false;
}
}
}
private static int putExclusiveTetromino(int row, int col) {
int sum = 0;
if (row - 1 >= 0 && col - 1 >= 0) {
// ㅜ
if (col + 1 < m) {
sum = Math.max(sum, arr[row][col] + arr[row - 1][col - 1] + arr[row - 1][col] + arr[row - 1][col + 1]);
}
// ㅏ
if (row + 1 < n) {
sum = Math.max(sum, arr[row][col] + arr[row - 1][col - 1] + arr[row][col - 1] + arr[row + 1][col - 1]);
}
}
if (row + 1 < n && col + 1 < m) {
// ㅗ
if (col - 1 >= 0) {
sum = Math.max(sum, arr[row][col] + arr[row + 1][col - 1] + arr[row + 1][col] + arr[row + 1][col + 1]);
}
// ㅓ
if (row - 1 >= 0) {
sum = Math.max(sum, arr[row][col] + arr[row - 1][col + 1] + arr[row][col + 1] + arr[row + 1][col + 1]);
}
}
return sum;
}
}
