BOJ 2533 사회망 서비스(SNS) (Java)

사람·2025년 4월 13일

BOJ

목록 보기

45/74

문제

https://www.acmicpc.net/problem/2533

페이스북, 트위터, 카카오톡과 같은 사회망 서비스(SNS)가 널리 사용됨에 따라, 사회망을 통하여 사람들이 어떻게 새로운 아이디어를 받아들이게 되는가를 이해하는 문제가 중요해졌다. 사회망에서 사람들의 친구 관계는 그래프로 표현할 수 있는데, 이 그래프에서 사람은 정점으로 표현되고, 두 정점을 잇는 에지는 두 정점으로 표현되는 두 사람이 서로 친구 관계임을 표현한다.

예를 들어, 철수와 영희, 철수와 만수, 영희와 순희가 서로 친구 관계라면 이를 표현하는 친구 관계 그래프는 다음과 같다.

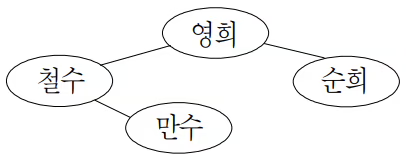
친구 관계 그래프를 이용하면 사회망 서비스에서 어떤 새로운 아이디어가 전파되는 과정을 이해하는데 도움을 줄 수 있다. 어떤 새로운 아이디어를 먼저 받아들인 사람을 얼리 아답터(early adaptor)라고 하는데, 사회망 서비스에 속한 사람들은 얼리 아답터이거나 얼리 아답터가 아니다. 얼리 아답터가 아닌 사람들은 자신의 모든 친구들이 얼리 아답터일 때만 이 아이디어를 받아들인다.

어떤 아이디어를 사회망 서비스에서 퍼뜨리고자 할 때, 가능한 한 최소의 수의 얼리 아답터를 확보하여 모든 사람이 이 아이디어를 받아들이게 하는 문제는 매우 중요하다.

일반적인 그래프에서 이 문제를 푸는 것이 매우 어렵다는 것이 알려져 있기 때문에, 친구 관계 그래프가 트리인 경우, 즉 모든 두 정점 사이에 이들을 잇는 경로가 존재하면서 사이클이 존재하지 않는 경우만 고려한다.

예를 들어, 8명의 사람으로 이루어진 다음 친구 관계 트리를 생각해보자. 2, 3, 4번 노드가 표현하는 사람들이 얼리 아답터라면, 얼리 아답터가 아닌 사람들은 자신의 모든 친구가 얼리 아답터이기 때문에 새로운 아이디어를 받아들인다.

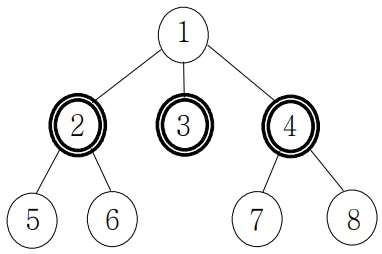
친구 관계 트리가 주어졌을 때, 모든 개인이 새로운 아이디어를 수용하기 위하여 필요한 최소 얼리 어답터의 수를 구하는 프로그램을 작성하시오.

입력
첫 번째 줄에는 친구 관계 트리의 정점 개수 N이 주어진다. 단, 2 ≤ N ≤ 1,000,000이며, 각 정점은 1부터 N까지 일련번호로 표현된다. 두 번째 줄부터 N-1개의 줄에는 각 줄마다 친구 관계 트리의 에지 (u, v)를 나타내는 두 정수 u와 v가 하나의 빈칸을 사이에 두고 주어진다.

출력
주어진 친구 관계 그래프에서 아이디어를 전파하는데 필요한 얼리 아답터의 최소 수를 하나의 정수로 출력한다.

예제 입력 1
8
1 2
1 3
1 4
2 5
2 6
4 7
4 8
예제 출력 1
3

예제 입력 2
9
1 2
1 3
2 4
3 5
3 6
4 7
4 8
4 9
예제 출력 2
3

1차 시도

접근

문제에 따르면 트리의 모든 노드는 아래의 두 가지 케이스 중 하나를 반드시 만족시켜야 한다.

자신이 직접 얼리어답터가 되든가.

자신을 제외한 모든 이웃 노드 (부모, 자식 노드)가 얼리어답터가 되든가.

그래서 문제를 보고 처음 한 생각은, (트리 특성상 루트를 제외한 모든 노드는 오직 1개의 부모만을 가질 수 있기에) 자식을 많이 갖고 있는 노드일수록 자기 자신이 직접 얼리어답터가 되는 게 유리할 거라는 거였다. 자식을 많이 갖고 있는 노드가 얼리어답터가 아니라면 그 모든 자식이 다 얼리어답터가 될 수밖에 없기 때문에 얼리어답터 수가 최소일 수 없겠다고 생각했다.

그래서 우선순위 큐를 사용해 이웃해 있는 노드 수가 가장 많은 노드 순으로 하나씩 차례로 꺼내서 해당 노드를 얼리어답터로 지정하는 방식을 사용해 구현해보았다. 이때 얼리어답터로 선택된 노드와 이웃해 있는 노드들의 경우에는 2번 케이스를 만족시키기 위해 필요한 이웃 얼리어답터가 1명 확보된 것이므로 이웃 노드에서 삭제함으로써 우선순위 큐에서 자신이 선택될 가능성(?)을 낮춰줬다.
위 과정을 반복하면서 얼리어답터 수를 1명씩 늘려 나가다가 문제의 조건을 모두 만족했다면 중단하고 출력을 했다.

구현

import java.io.*;
import java.util.*;

class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        List<Integer>[] tree = new List[N + 1];
        PriorityQueue<Integer> pq = new PriorityQueue<>((o1, o2) -> tree[o2].size() - tree[o1].size());
        for (int i = 1; i <= N; i++) {
            tree[i] = new ArrayList<>();
        }
        for (int i = 0; i < N - 1; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int u = Integer.parseInt(st.nextToken());
            int v = Integer.parseInt(st.nextToken());
            tree[u].add(v);
            tree[v].add(u);
        }
        for (int i = 1; i <= N; i++) {
            pq.offer(i);
        }

        int result = 0; 
        int spreadCount = 0; // 새로운 아이디어를 수용한 사람 수
        while (spreadCount < N) { 
            int curr = pq.poll(); // 새롭게 추가된 얼리어답터
            result++;
            spreadCount++;
            for (int friend : tree[curr]) {
                // 새로운 얼리어답터와 이웃해 있는 노드 - 새로운 얼리어답터 사이의 관계를 끊음
                tree[friend].remove(tree[friend].indexOf(curr));
                
                // friend와 이웃한 노드가 모두 얼리어답터가 된 경우
                // friend는 새로운 아이디어를 수용하게 됨.
                if (tree[friend].isEmpty()) {
                    spreadCount++;
                }
                
                // 우선순위 큐 재정렬
                pq.remove(friend);
                pq.offer(friend);
            }
        }

        System.out.println(result);
    }
}

이 구현에서 제일 나를 열받게 했던 점은, 우선순위 큐는 그 특성상 큐에 원소를 추가 혹은 삭제할 때만 정렬이 일어나는데

for (int friend : tree[curr]) {
    // 새로운 얼리어답터와 이웃해 있는 노드 - 새로운 얼리어답터 사이의 관계를 끊음
    tree[friend].remove(tree[friend].indexOf(curr));
}

위 코드 부분 (새롭게 선택된 얼리어답터와 이웃해있는 모든 노드들에 대해 얼리어답터와의 관계를 끊는 부분)은 우선순위 큐의 정렬 조건인 tree의 크기를 변경하고 있음에도 pq 원소에 대한 추가, 삭제는 발생하지 않아 다음 얼리어답터를 뽑을 때 이 변경 사항이 반영되지 않는다는 거였다. 그래서 우선순위 큐가 제대로 정렬되지 않은 상태라 이웃 노드 수가 최대인 노드가 제대로 선택되지 않았다.

// 우선순위 큐 재정렬
pq.remove(friend);
pq.offer(friend);

그래서 이 문제를 해결하기 위해 우선순위 큐에 있는 기존 원소를 삭제한 후 다시 넣는 코드를 추가함으로써 원소의 추가, 삭제를 발생시켜 정렬이 일어나도록 했다.

1차 시도의 문제점

하지만 결과적으로 이 방법으로는 문제를 풀 수가 없었다.

이 문제는 이와 같은 그리디한 방식으로 얼리 어답터를 선택하는 것이 최적해임이 보장되어 있지가 않다.
~~요즘 우선순위 큐의 저주에 걸린 건지 우선순위 큐로 풀면 다 틀린다...~~
시간 복잡도

while (spreadCount < N) {
    int curr = pq.poll();               // O(log N)
    ...
    for (int friend : tree[curr]) {     // 최악의 경우 O(N)
        tree[friend].remove(...);       // 최악의 경우 O(N)
        pq.remove(friend);              // O(N)
        pq.offer(friend);               // O(log N)
    }
}

pq.poll() → O(log N)
tree[friend].remove(...) → 리스트에서 값 제거 → 최악의 경우 O(N)
pq.remove(friend) → 리스트에서 임의 값 제거 → O(N)
pq.offer(friend) → O(log N)

최악의 경우 시간 복잡도가 O(N^2)에 가까워지기에 시간 초과가 발생한다.

2차 시도

접근

다른 접근법은 더 이상 떠오르지가 않아서 알고리즘 분류를 보고, DP로 풀어야 한다는 사실을 알게 되었다...
예전에 간단한 트리 DP 문제를 한 번 풀어본 적이 있어서 그래도 구현 방식 자체는 조금 수월하게 감을 잡았다.

dp[i]에 i번 노드를 루트로 하는 서브트리에서의 최소 얼리어답터 수를 저장하는 식으로 구현하면 될 것 같다고 생각했다.
이 값은 i번 노드가 얼리어답터인지 여부 (얼리어답터라면 1, 아니라면 0) + i번 노드의 자식을 루트로 하는 모든 서브트리에서의 최소 얼리어답터 수의 총합
이기에 부분합, 즉 DP로 해결할 수 있으니까.

그리고 i번 노드가 얼리어답터인지 여부는 부모 노드가 얼리어답터인지 여부에 따라 달라질 것이다.

부모가 얼리어답터였다면
: 자신은 얼리어답터여도 되고, 아니어도 된다.
-> 두 경우를 모두 구한 후 필요한 얼리어답터 수가 더 작은 경우를 채택한다.

부모가 얼리어답터가 아니었다면
: 자신은 반드시 얼리어답터여야 문제의 조건을 만족시킨다.

구현

import java.io.*;
import java.util.*;

class Main {
    static int N;
    static List<Integer>[] tree;
    static int[] dp;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        tree = new List[N + 1];
        dp = new int[N + 1]; // dp[i]: i번 노드를 루트로 하는 서브 트리에서 필요한 최소 얼리 어답터 수
        Arrays.fill(dp, -1);
        for (int i = 0; i <= N; i++) {
            tree[i] = new ArrayList<>();
        }
        for (int i = 0; i < N - 1; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int u = Integer.parseInt(st.nextToken());
            int v = Integer.parseInt(st.nextToken());
            tree[u].add(v);
            tree[v].add(u);
        }
        tree[1].add(0);
        dynamicProgramming(1, 0, true);
        System.out.println(dp[1]);
    }

    private static int dynamicProgramming(int subRoot, int parent, boolean isEarlyAdopter) {
    	// 리프 노드인 경우
        if (tree[subRoot].size() == 1) {
            return (isEarlyAdopter)? 0 : 1;
        }
        
        // 부모가 얼리어답터이면 자신은 얼리어답터여도 되고, 아니어도 됨.
        // 부모가 얼리어답터가 아니라면 자신은 반드시 얼리어답터여야 함.
        if (dp[subRoot] == -1) {
            // 자신이 루트 노드이거나 자신의 부모가 얼리어답터인 경우
            if (isEarlyAdopter) {
                dp[subRoot] = 0;
                // 자신도 얼리어답터인 경우
                int temp1 = 1;
                // 자신은 얼리어답터가 아닌 경우
                int temp2 = 0;
                for (int neighbor : tree[subRoot]) {
                    if (neighbor == parent) {
                        continue;
                    }
                    temp2 += dynamicProgramming(neighbor, subRoot, false);
                    temp1 += dynamicProgramming(neighbor, subRoot, true);
                }
                dp[subRoot] = Math.min(temp1, temp2);
            } else { // 부모가 얼리어답터가 아닌 경우
                dp[subRoot] = 1; // 자신은 무조건 얼리어답터여야 함
                for (int neighbor : tree[subRoot]) {
                    if (neighbor == parent) {
                        continue;
                    }
                    dp[subRoot] += dynamicProgramming(neighbor, subRoot, true);
                }
            }
        }

        return dp[subRoot];
    }
}

2차 시도의 문제점

하지만 이때도 일부 테스트 케이스에서 답이 조금씩 차이가 났다.

temp2 += dynamicProgramming(neighbor, subRoot, false);
temp1 += dynamicProgramming(neighbor, subRoot, true);

특히 위 두 코드의 순서를 바꿈에 따라 정답이 되기도 하고, 오답이 되기도 했다.
그러니까 호출 순서에 따라 dp 배열의 값에 충돌이 발생하고 있는 거다.
이 부분이 문제라는 건 알았는데 아무리 디버깅을 해봐도 어디를 바꿔야 할지 감이 안 왔다. 이 정도는 알아낼 수 있어야 했는데, 지금 와서 보니 좀 아쉽다...
암튼간에 이미 여기까지 하는 데 며칠을 썼기 때문에, 더 이상 지체할 수 없어 챗지피티에게 점화식을 부탁해서 최종 구현을 했다.

2차 시도에서 부모 노드가 얼리어답터인지 여부에 따라 자식의 상태가 달라지는 것까지는 잘 파악했다. 하지만 문제는 dp[subRoot]를 isEarlyAdopter 상태와 관계없이 단일 값으로 관리하고 있다는 점이었다.
이 dp 배열은 subRoot가 얼리어답터인지 여부에 따라 결과가 다르다. 하지만 나는 그럼에도 두 경우 중 단 하나의 값만 저장하고 있었다. 이 때문에 dynamicProgramming(neighbor, subRoot, false)와 dynamicProgramming(neighbor, subRoot, true)를 연달아 호출했을 때 캐싱 결과가 충돌해 순서에 따라 값이 달라지는 문제가 생기는 거였다.

3차 시도 (최종 풀이)

즉, 이 문제는 부모가 얼리어답터일 때, 얼리어답터가 아닐 때를 나누어 이차원 배열에 메모이제이션을 했어야 했던 거다.

dp[node][0]
: 해당 노드가 얼리어답터 아닐 때 해당 노드를 루트로 하는 서브트리의 최소 얼리어답터 수
dp[node][1]
: 해당 노드가 얼리어답터일 때 해당 노드를 루트로 하는 서브트리의 최소 얼리어답터 수
dp[node][1] = 1 + ∑ min(dp[child][0], dp[child][1]) // 내가 얼리어답터 → 자식은 자유
dp[node][0] = ∑ dp[child][1] // 내가 얼리어답터 아님 → 자식은 모두 얼리어답터

이렇게 말이다.

몇 차원 배열을 써야 하는지 이건 참... 언제 봐도 헷갈리는 부분이라 뭘 어떻게 해야 할지 모르겠다. 요즘 1차원 문제를 많이 푸니까 그냥 너무 당연하게 그렇게 접근했던 거 같다. 2, 3차원 dp 문제도 많이 풀어봐야 될 것 같다.

import java.io.*;
import java.util.*;

class Main {
    static int N;
    static List<Integer>[] tree;
    static int[][] dp;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        tree = new List[N + 1];
        // dp[i]: i번 노드를 루트로 하는 서브 트리에서 필요한 최소 얼리 어답터 수
        dp = new int[N + 1][2]; 
        for (int i = 1; i <= N; i++) {
            tree[i] = new ArrayList<>();
            Arrays.fill(dp[i], -1);
        }
        for (int i = 0; i < N - 1; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int u = Integer.parseInt(st.nextToken());
            int v = Integer.parseInt(st.nextToken());
            tree[u].add(v);
            tree[v].add(u);
        }
        tree[1].add(0);
        System.out.println(dynamicProgramming(1, 0, true));
    }

    private static int dynamicProgramming(int subRoot, int parent, boolean isEarlyAdopter) {
        // 리프 노드인 경우
        if (tree[subRoot].size() == 1) {
            return (isEarlyAdopter)? 0 : 1;
        }

        // 자신의 부모 노드가 얼리어답터인 경우: 자신은 얼리어답터여도 되고, 아니어도 됨.
        if (isEarlyAdopter) {
            if (dp[subRoot][0] == -1 || dp[subRoot][1] == -1) {
                int temp0 = 0; // 자신은 얼리어답터가 아닌 경우
                int temp1 = 1; // 자신도 얼리 어답터인 경우
                for (int neighbor : tree[subRoot]) {
                    if (neighbor == parent) {
                        continue;
                    }
                    temp0 += dynamicProgramming(neighbor, subRoot, false);
                    temp1 += dynamicProgramming(neighbor, subRoot, true);
                }
                dp[subRoot][0] = (dp[subRoot][0] == -1)? temp0 : dp[subRoot][0];
                dp[subRoot][1] = (dp[subRoot][1] == -1)? temp1 : dp[subRoot][1];
            }
        }
        // 자신의 부모가 얼리 어답터가 아닌 경우: 자신은 무조건 얼리어답터여야 함.
        else {
            if (dp[subRoot][1] == -1) {
                dp[subRoot][1] = 1;
                for (int neighbor : tree[subRoot]) {
                    if (neighbor == parent) {
                        continue;
                    }
                    dp[subRoot][1] += dynamicProgramming(neighbor, subRoot, true);
                }
            }
            return dp[subRoot][1];
        }

        return Math.min(dp[subRoot][0], dp[subRoot][1]);
    }
}