문제

https://www.acmicpc.net/problem/14719
2차원 세계에 블록이 쌓여있다. 비가 오면 블록 사이에 빗물이 고인다.

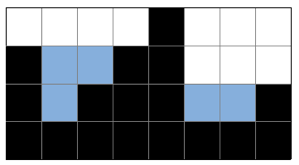
비는 충분히 많이 온다. 고이는 빗물의 총량은 얼마일까?

입력
첫 번째 줄에는 2차원 세계의 세로 길이 H과 2차원 세계의 가로 길이 W가 주어진다. (1 ≤ H, W ≤ 500)

두 번째 줄에는 블록이 쌓인 높이를 의미하는 0이상 H이하의 정수가 2차원 세계의 맨 왼쪽 위치부터 차례대로 W개 주어진다.

따라서 블록 내부의 빈 공간이 생길 수 없다. 또 2차원 세계의 바닥은 항상 막혀있다고 가정하여도 좋다.

출력
2차원 세계에서는 한 칸의 용량은 1이다. 고이는 빗물의 총량을 출력하여라.

빗물이 전혀 고이지 않을 경우 0을 출력하여라.

예제 입력 1
4 4
3 0 1 4
예제 출력 1
5

예제 입력 2
4 8
3 1 2 3 4 1 1 2
예제 출력 2
5

예제 입력 3
3 5
0 0 0 2 0
예제 출력 3
0

힌트
힌트 1:

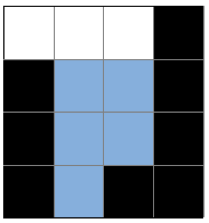
힌트 2:

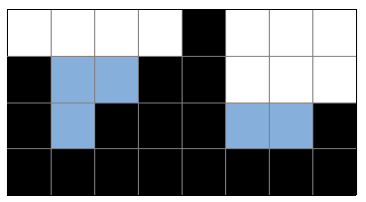
힌트 3:

---

접근

처음에 단순하게 생각했다가 생각보다 고려할 게 많아서 좀 헤맸다...
빗물이 고이기 시작하는 블록보다 높이가 높거나 같은 블록이 나올 때까지 빗물이 고일 것이다.

이렇게 말이다.
그리고 각 열마다 빗물이 고이는 양은 (시작 블록의 높이) - (현재 블록의 높이)이다. 이 값을 temp라는 int 타입 변수에 누적해 나가다가, 높이가 시작 블록 이상인 블록에 도달하면 이 temp 값을 sum에 모두 더해주는 식으로 구현하려고 했다.

그런데 문제가 있었다.

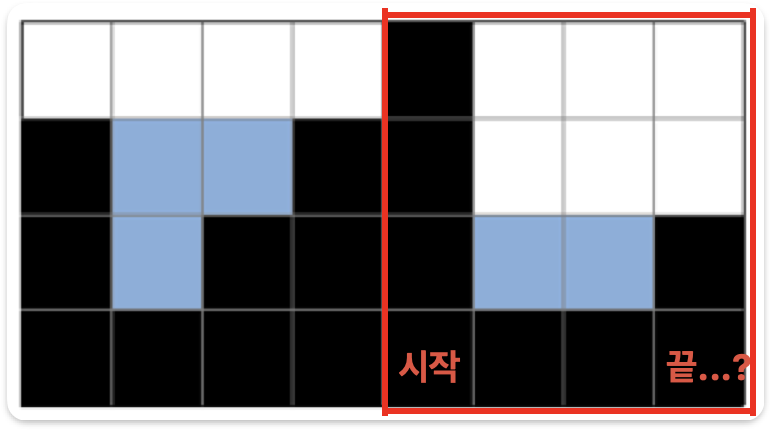
위 케이스처럼 시작 블록 이상의 높이를 가지는 블록이 마지막까지 나오지 않는 경우가 있을 수 있다는 것이다.
하지만 왼쪽에서 오른쪽으로 선형 탐색을 해나가는 와중에 뒤에 그런 블록이 존재할지 안 할지 예측할 수도 없는 거고.
이 경우를 어떻게 처리해야 할지를 고민하는 데 좀 오래 걸렸다.

그러다가, 시작 블록 이상의 높이를 가지는 블록이 무조건 존재하도록 탐색 방향을 바꿔보면 되지 않을까? 하는 생각을 하게 됐다.

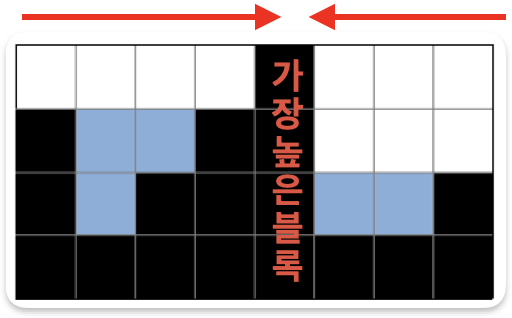
일단 입력을 받을 때, 블록 중 최댓값의 위치를 찾아 저장해 둔다.
그리고 그 최대 높이 블록에 도달할 때까지는 왼쪽 끝에서 오른쪽으로 탐색을 하고, 그 후에는 오른쪽 끝에서 이 최대 높이 블록까지 탐색을 하는 거다. 이렇게 하면 시작 블록 뒤에는 항상 자신보다 크거나 같은 블록이 존재할 수밖에 없게 된다.
그러므로, 이렇게 하면 자신보다 크거나 같은 블록이 나타날 때까지 temp에 현재 열에 고일 빗물의 양, 즉 (시작 블록의 높이) - (현재 블록의 높이) 값을 계속 누적하다가, 나타나면 그때 이 temp 값을 sum에 누적하는 방식으로 구현이 가능하다.

구현

import java.io.*;
import java.util.*;

class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        st.nextToken(); // H 값은 쓸 데가 없다...
        int W = Integer.parseInt(st.nextToken());
        int[] blocks = new int[W];
        
        int maxBlock = -1;
        int maxBlockIdx = 0;
        st = new StringTokenizer(br.readLine());
        for (int i = 0; i < W; i++) {
            blocks[i] = Integer.parseInt(st.nextToken());
            if (blocks[i] > maxBlock) {
                maxBlock = blocks[i];
                maxBlockIdx = i;
            }
        }

        boolean flag = false; // 시작 부분이 막혀있는지 여부 저장
        int init = 0;
        int sum = 0;
        int temp = 0;
        
        // 최대 높이의 블록이 나올 때까지는 왼쪽에서 오른쪽으로 탐색
        for (int i = 0; i <= maxBlockIdx; i++) {
            if (flag) {
                if (blocks[i] >= blocks[init]) {
                    sum += temp;
                    init = i;
                    temp = 0;
                } else {
                    temp += (blocks[init] - blocks[i]);
                }
            } else {
                if (blocks[i] == 0) {
                    continue;
                }
                flag = true;
                init = i;
            }
        }

        flag = false;
        init = W - 1;
        temp = 0;
        // 오른쪽에서 왼쪽으로 최대 높이의 블록이 나올 때까지 탐색
        for (int i = W - 1; i >= maxBlockIdx; i--) {
            if (flag) {
                if (blocks[i] >= blocks[init]) {
                    sum += temp;
                    init = i;
                    temp = 0;
                } else {
                    temp += (blocks[init] - blocks[i]);
                }
            } else {
                if (blocks[i] == 0) {
                    continue;
                }
                flag = true;
                init = i;
            }
        }

        System.out.println(sum);
    }
}

찾아보니까 다르게 푸신 분들도 많더라...!