문제

https://www.acmicpc.net/problem/17471

백준시의 시장 최백준은 지난 몇 년간 게리맨더링을 통해서 자신의 당에게 유리하게 선거구를 획정했다. 견제할 권력이 없어진 최백준은 권력을 매우 부당하게 행사했고, 심지어는 시의 이름도 백준시로 변경했다. 이번 선거에서는 최대한 공평하게 선거구를 획정하려고 한다.

백준시는 N개의 구역으로 나누어져 있고, 구역은 1번부터 N번까지 번호가 매겨져 있다. 구역을 두 개의 선거구로 나눠야 하고, 각 구역은 두 선거구 중 하나에 포함되어야 한다. 선거구는 구역을 적어도 하나 포함해야 하고, 한 선거구에 포함되어 있는 구역은 모두 연결되어 있어야 한다. 구역 A에서 인접한 구역을 통해서 구역 B로 갈 수 있을 때, 두 구역은 연결되어 있다고 한다. 중간에 통하는 인접한 구역은 0개 이상이어야 하고, 모두 같은 선거구에 포함된 구역이어야 한다.

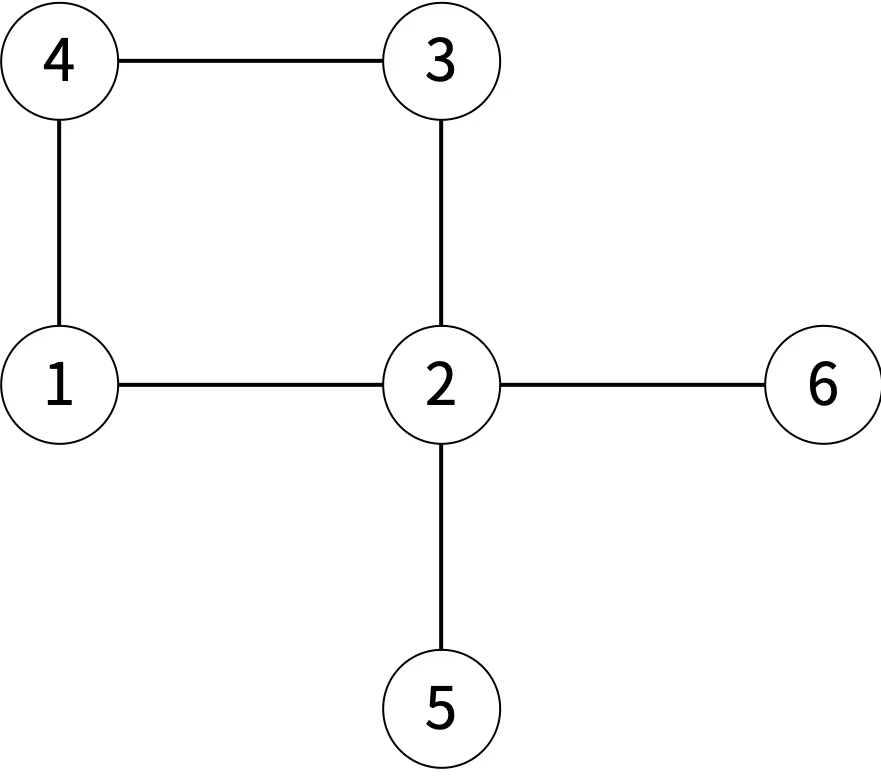
아래 그림은 6개의 구역이 있는 것이고, 인접한 구역은 선으로 연결되어 있다.

아래는 백준시를 두 선거구로 나눈 4가지 방법이며, 가능한 방법과 불가능한 방법에 대한 예시이다.

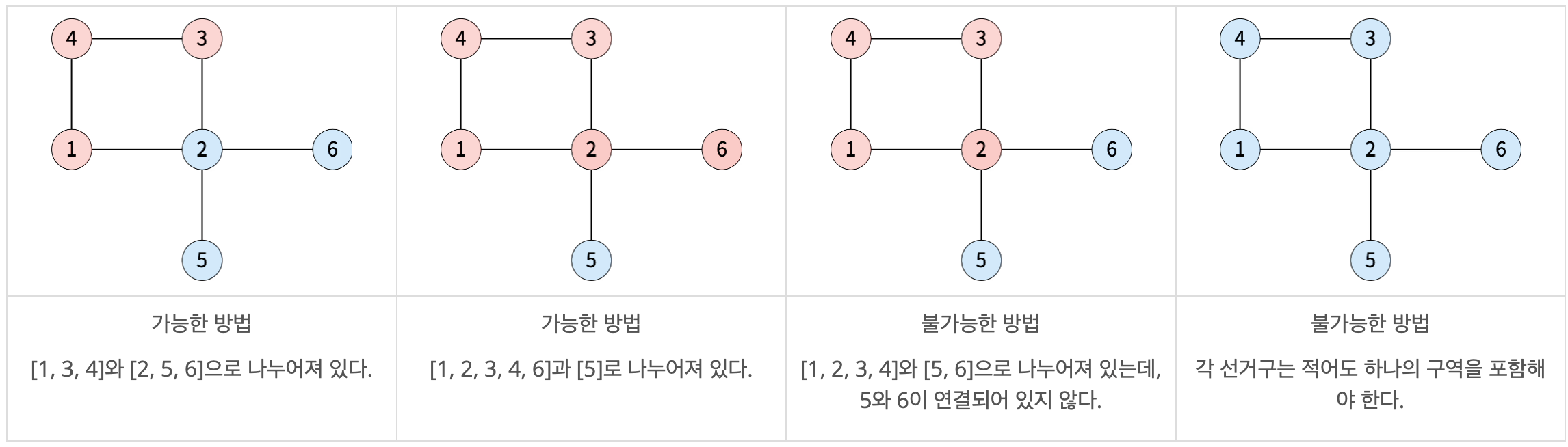
공평하게 선거구를 나누기 위해 두 선거구에 포함된 인구의 차이를 최소로 하려고 한다. 백준시의 정보가 주어졌을 때, 인구 차이의 최솟값을 구해보자.

입력
첫째 줄에 구역의 개수 N이 주어진다. 둘째 줄에 구역의 인구가 1번 구역부터 N번 구역까지 순서대로 주어진다. 인구는 공백으로 구분되어져 있다.

셋째 줄부터 N개의 줄에 각 구역과 인접한 구역의 정보가 주어진다. 각 정보의 첫 번째 정수는 그 구역과 인접한 구역의 수이고, 이후 인접한 구역의 번호가 주어진다. 모든 값은 정수로 구분되어져 있다.

구역 A가 구역 B와 인접하면 구역 B도 구역 A와 인접하다. 인접한 구역이 없을 수도 있다.

출력
첫째 줄에 백준시를 두 선거구로 나누었을 때, 두 선거구의 인구 차이의 최솟값을 출력한다. 두 선거구로 나눌 수 없는 경우에는 -1을 출력한다.

제한
2 ≤ N ≤ 10
1 ≤ 구역의 인구 수 ≤ 100

예제 입력 1
6
5 2 3 4 1 2
2 2 4
4 1 3 6 5
2 4 2
2 1 3
1 2
1 2
예제 출력 1
1
선거구를 [1, 4], [2, 3, 5, 6]으로 나누면 각 선거구의 인구는 9, 8이 된다. 인구 차이는 1이고, 이 값보다 더 작은 값으로 선거구를 나눌 수는 없다.

예제 입력 2
6
1 1 1 1 1 1
2 2 4
4 1 3 6 5
2 4 2
2 1 3
1 2
1 2
예제 출력 2
0
선거구를 [1, 3, 4], [2, 5, 6]으로 나누면 인구 차이가 0이다.

예제 입력 3
6
10 20 10 20 30 40
0
0
0
0
0
0
예제 출력 3
-1
두 선거구로 나눌 수 있는 방법이 없다.

예제 입력 4
6
2 3 4 5 6 7
2 2 3
2 1 3
2 1 2
2 5 6
2 4 6
2 4 5
예제 출력 4
9

접근

아 처음에 너무 이상하게 접근해서 시간을 너무 많이 버렸다...ㅜㅜ
그냥 백트래킹 하면서 구역을 일단 둘로 쪼갠 다음에 쪼개기가 끝나면 마지막에만 각 구역이 서로 연결되어 있는지 확인하면 코드도 훨씬 간단하고 시간 복잡도 면에서도 더 효율적인데, 처음부터 연결되어 있는 애들끼리 선택하려고 하다보니까 매 선택마다 연결 여부를 확인하는 미친 짓을 하다가 코드를 엎었다...^^ 아 너무 바보 같다.
생각을 좀 하면서 풀어야겠다고 생각했다.

구현

import java.io.*;
import java.util.*;

class Main {
    static int N;
    static int result = Integer.MAX_VALUE;
    static int[] population;
    static List<Integer>[] graph;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        population = new int[N + 1];
        graph = new List[N + 1];
        StringTokenizer st = new StringTokenizer(br.readLine());

        for (int n = 1; n <= N; n++) {
            population[n] = Integer.parseInt(st.nextToken());
            graph[n] = new ArrayList<>();
        }

        for (int n = 1; n <= N; n++) {
            st = new StringTokenizer(br.readLine());
            int total = Integer.parseInt(st.nextToken());
            for (int i = 0; i < total; i++) {
                int neighbor = Integer.parseInt(st.nextToken());
                graph[n].add(neighbor);
                graph[neighbor].add(n);
            }
        }

        backtracking(1, new ArrayList<>(), new ArrayList<>(), 0, 0);

        if (result == Integer.MAX_VALUE) {
            System.out.println(-1);
            return;
        }
        System.out.println(result);
    }

    private static void backtracking(int depth, List<Integer> A, List<Integer> B, int sumOfA, int sumOfB) {
        if (depth > N) {
            if (isConnected(A, B)) {
                result = Math.min(result, Math.abs(sumOfA - sumOfB));
            }
            return;
        }

        A.add(depth);
        sumOfA += population[depth];
        backtracking(depth + 1, A, B, sumOfA, sumOfB);

        A.remove(A.size() - 1);
        sumOfA -= population[depth];
        B.add(depth);
        sumOfB += population[depth];
        backtracking(depth + 1, A, B, sumOfA, sumOfB);
        B.remove(B.size() - 1);
    }

    private static boolean isConnected(List<Integer> A, List<Integer> B) {
        if (A.isEmpty() || B.isEmpty()) {
            return false;
        }
        
        Queue<Integer> q = new LinkedList<>();
        Set<Integer> set = new HashSet<>(A);
        q.offer(A.get(0));
        set.remove(A.get(0));
        while (!q.isEmpty()) {
            int curr = q.poll();
            for (int neighbor : graph[curr]) {
                if (!set.contains(neighbor)) {
                    continue;
                }
                set.remove(neighbor);
                q.offer(neighbor);
            }
        }
        if (!set.isEmpty()) {
            return false;
        }

        set.addAll(B);
        q.offer(B.get(0));
        set.remove(B.get(0));
        while (!q.isEmpty()) {
            int curr = q.poll();
            for (int neighbor : graph[curr]) {
                if (!set.contains(neighbor)) {
                    continue;
                }
                set.remove(neighbor);
                q.offer(neighbor);
            }
        }
        return set.isEmpty();
    }
}