문제
https://www.acmicpc.net/problem/1749
동주는 항상 혼자 노느라 심심하다. 하지만 혼자 놀기의 고수가 된 동주는 매일매일 게임을 개발하여 혼자놀기의 진수를 우리에게 보여준다. 어느 날 동주는 새로운 게임을 개발하였다. 바로 점수 따먹기라는 게임인데 그다지 재밌어 보이지는 않는다.
동주가 개발한 게임은 이렇다. 일단 N*M 행렬을 그린 다음, 각 칸에 -10,000 이상 10,000 이하의 정수를 하나씩 쓴다. 그런 다음 그 행렬의 부분행렬을 그려 그 안에 적힌 정수의 합을 구하는 게임이다.
동주가 혼자 재밌게 놀던 중 지나가는 당신을 보고 당신을 붙잡고 게임을 하자고 한다. 귀찮은 당신은 정수의 합이 최대가 되는 부분행렬을 구하여 빨리 동주에게서 벗어나고 싶다.
입력
첫째 줄에 N (1 < N < 200), M (1 < M < 200)이 주어진다. 그 다음 N개의 줄에 M개씩 행렬의 원소가 주어진다.
출력
첫째 줄에 최대의 합을 출력하라.
예제 입력 1
3 5
2 3 -21 -22 -23
5 6 -22 -23 -25
-22 -23 4 10 2
예제 출력 1
16
접근
동주야 한 번만 더 말 걸면 죽인다 진짜
일단 이 문제는 보자마자 DP로 풀어야 할 것 같은 느낌이 막연히 들었다. 그런데 누적 합을 구한 다음에 DP를 했어야 했는데 그냥 무지성 DP를 하려고 하니까 '?? 하위 문제가 중복되지가 않는데 뭐지??' 이러고 있었다.
사실 이 문제는 (1, 1)에서 (i, j)까지의 누적 합을 일단 싹 다 구해서 배열에 저장해둔 다음 이 값들을 재사용해가는 방식으로 부분행렬의 합을 구했어야만 했다.
일단 (1, 1)에서 (i, j)까지의 누적 합을 구하는 방법을 알아보자.
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
// ...
}
}위와 같은 이중 for문을 통해 i와 j를 차례로 증가시켜가며 누적 합을 순차적으로 구하려고 한다.
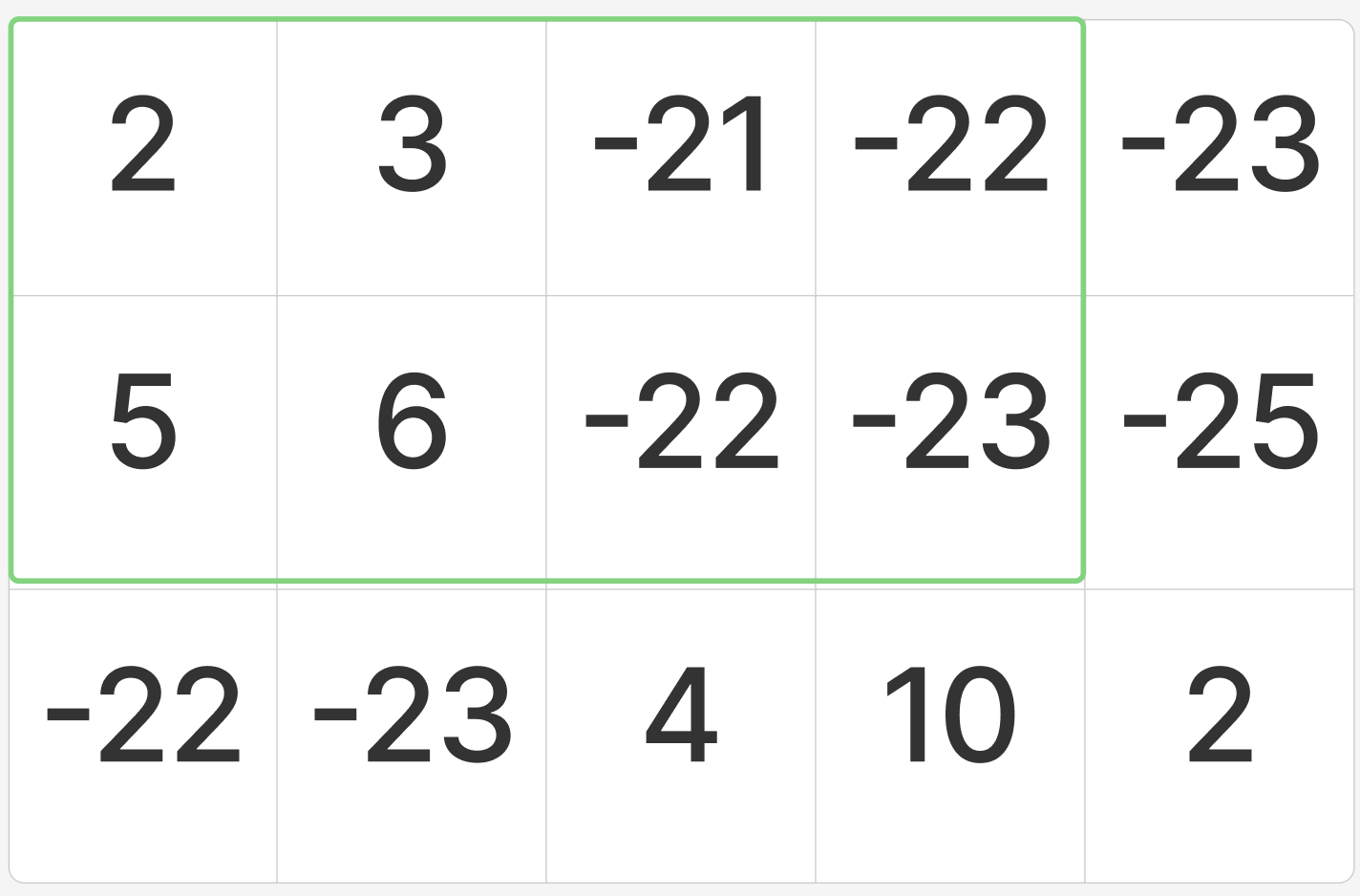
문제에 주어진 예제에서 (1, 1)부터 (2, 4)까지, 즉 위 사진에서 초록색으로 표시된 부분의 합을 구하려고 한다고 생각해보자.
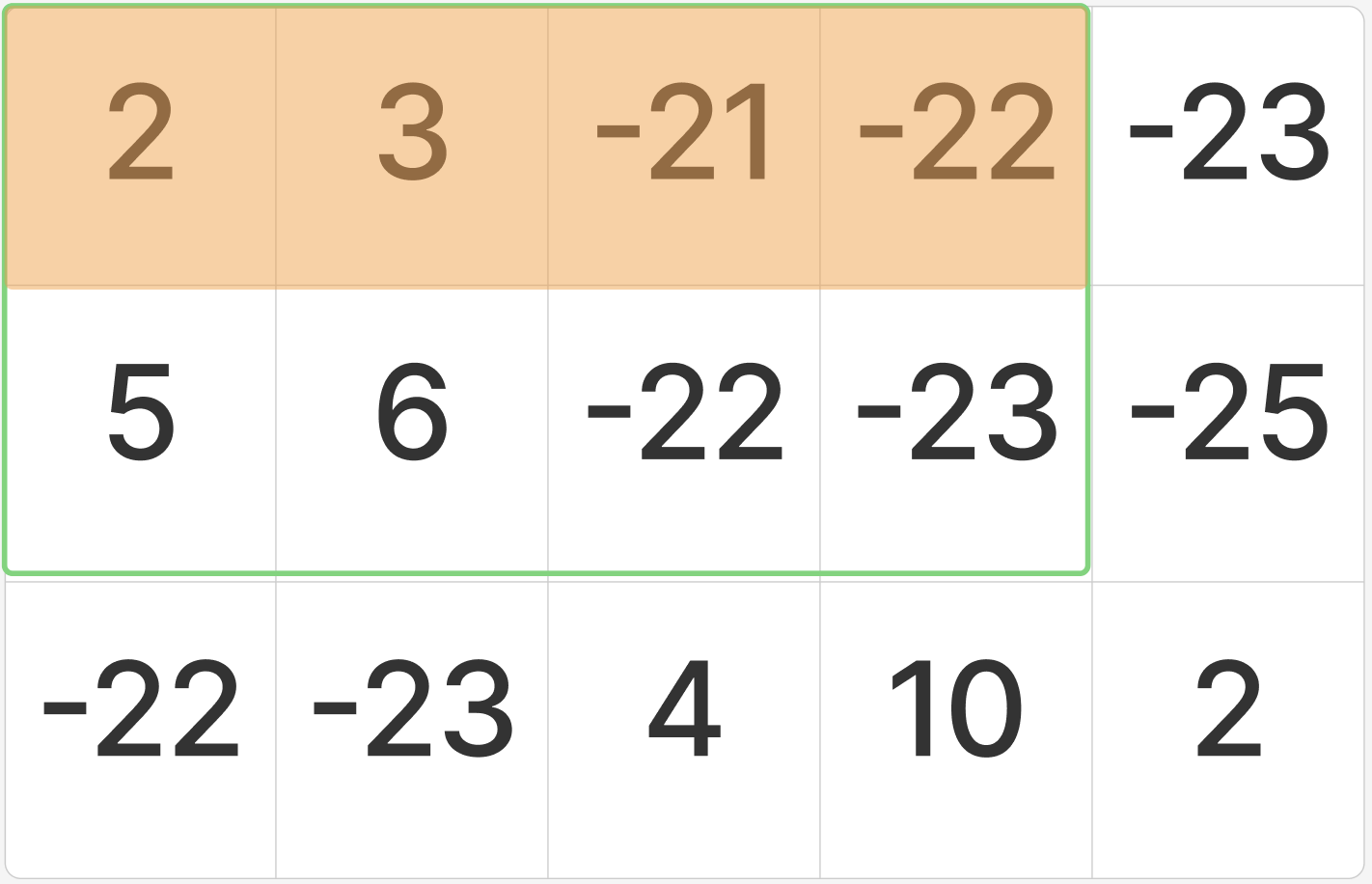
일단 위 사진에서 노란색으로 칠해진 부분의 합은 이미 앞에서 구한 상태일 것이다.
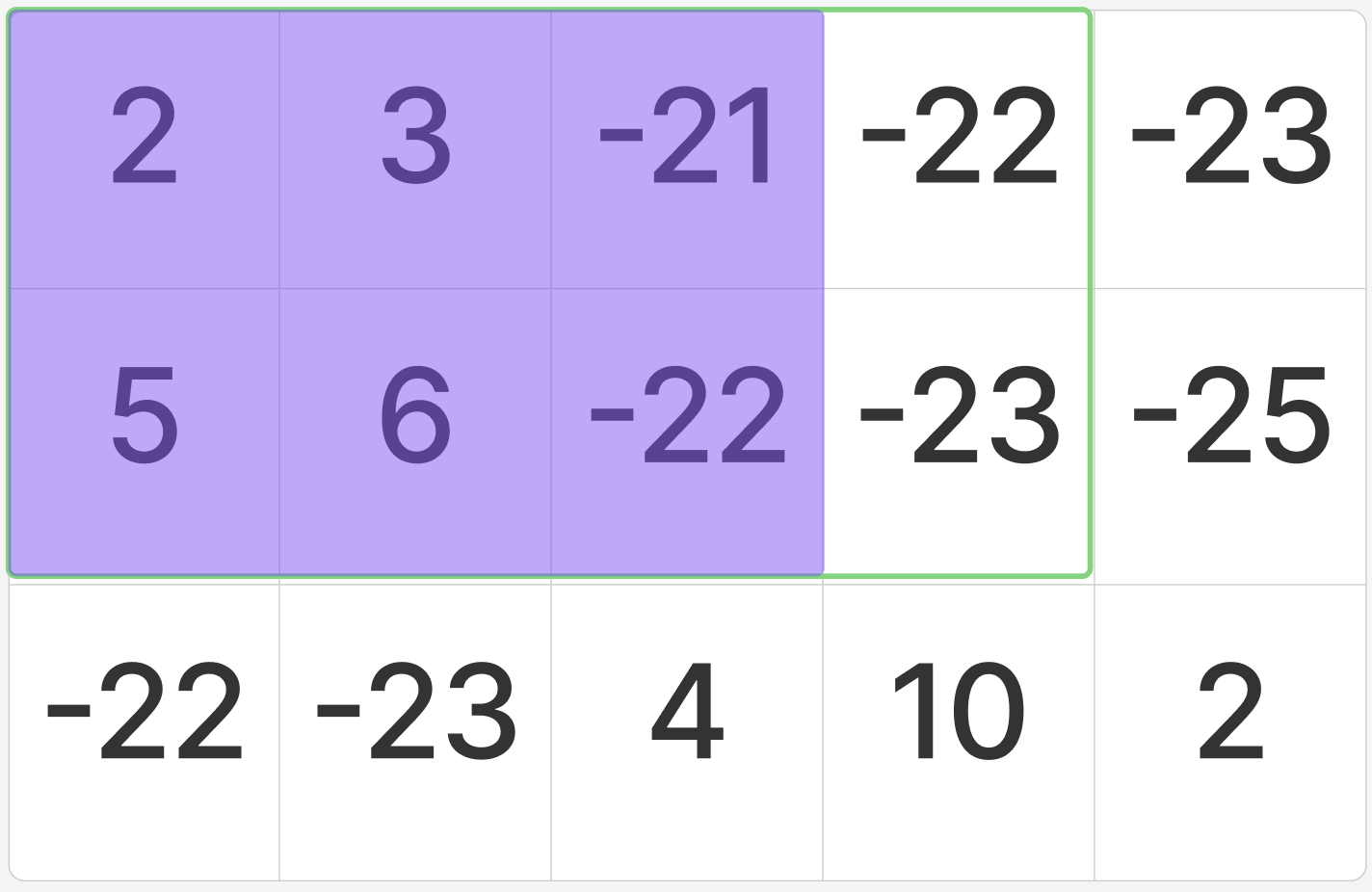
위 사진에서 보라색으로 칠해진 부분의 합도 이미 앞에서 구한 상태일 것이다. 앞에서 본 노란색 부분의 합과 위 보라색 부분의 합을 더해준다.
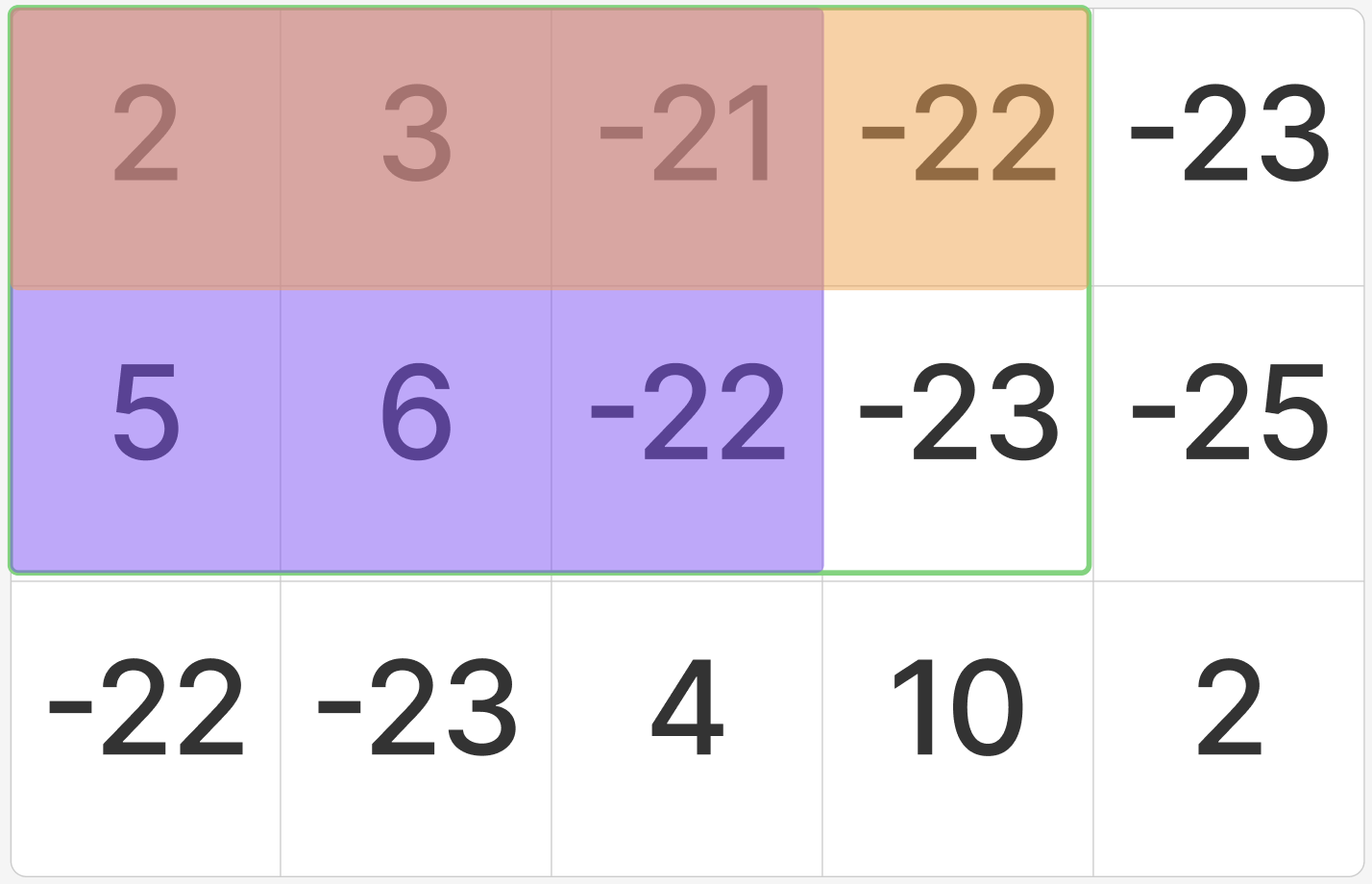
그런데 이 두 부분 사이에는 중복이 있다. 중복된 부분은 두 번 더해졌을 것이므로 한 번 빼줘야 한다.
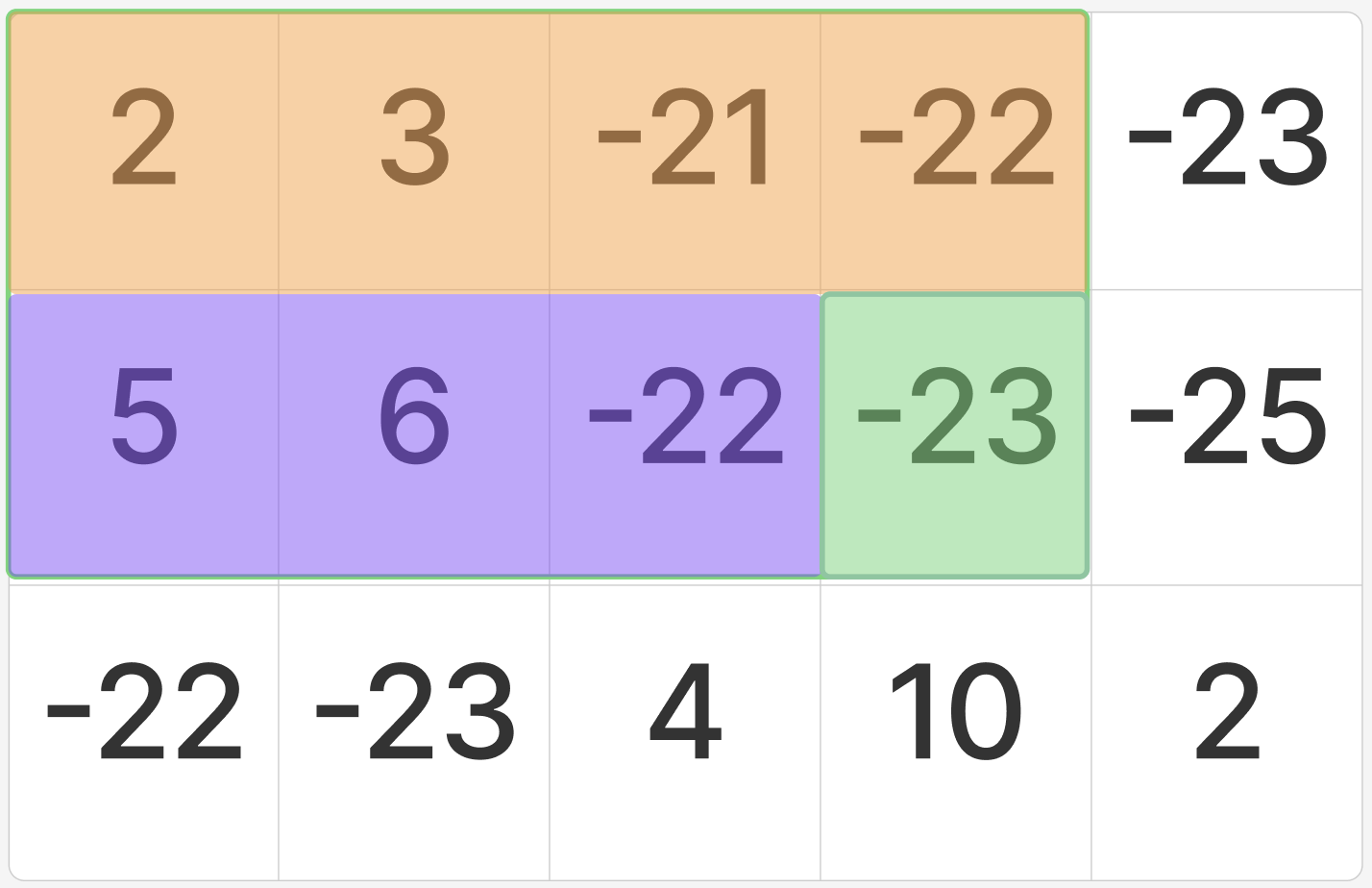
마지막으로 자기 자신을 더해주면 (1, 1)부터 자기 자신까지의 합이 완성된다.
이걸 일반화하여 식을 세우면, 자기 자신을 num이라고 할 때 (1, 1)부터 num까지의 합은
sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + num
가 된다.
이렇게 (1, 1)부터 모든 위치까지의 합을 구했다면, (1, 1)부터 시작하지 않는 부분행렬이더라도 부분합을 다음과 같이 구할 수 있다.
위에서 본 방식과 비슷하다.
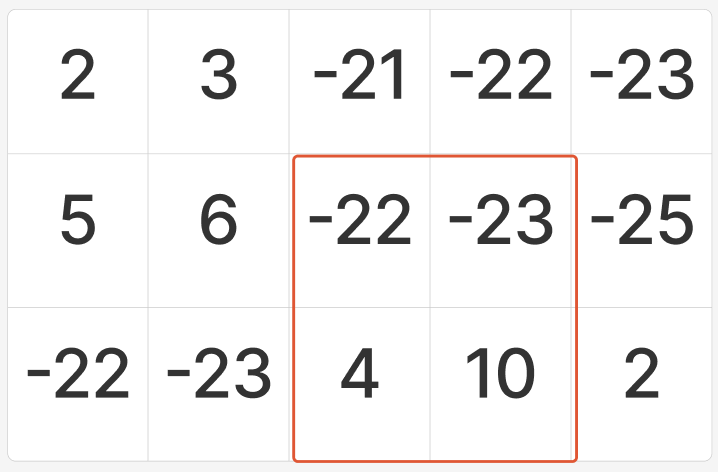
예를 들어 문제에 나온 예제에서 위 빨간 네모 부분, 즉 (2, 3)에서 (3, 4)까지 행렬에 대한 부분합을 구하려고 한다고 생각해 보자.

일단 보라색으로 칠해진 부분, 즉 (1, 1)에서 (3, 4)까지의 합을 가져온다.

그 다음, 위 사진에서 빨간색으로 칠해진 부분, 즉 (1, 1)에서 (3, 2)까지의 합은 구하려고 하는 부분 행렬 범위 밖에 있으므로 빼준다.
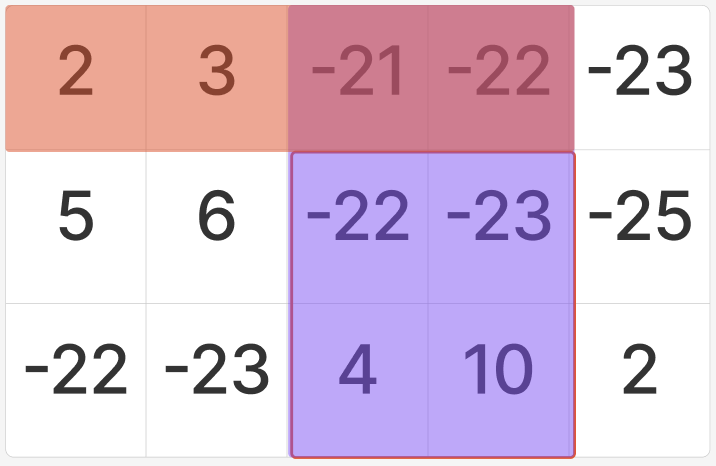
위 사진에서 빨간색으로 칠해진 부분, 즉 (1, 1)에서 (1, 4)까지의 합 역시 구하려고 하는 부분행렬 범위 밖에 있으므로 빼준다.
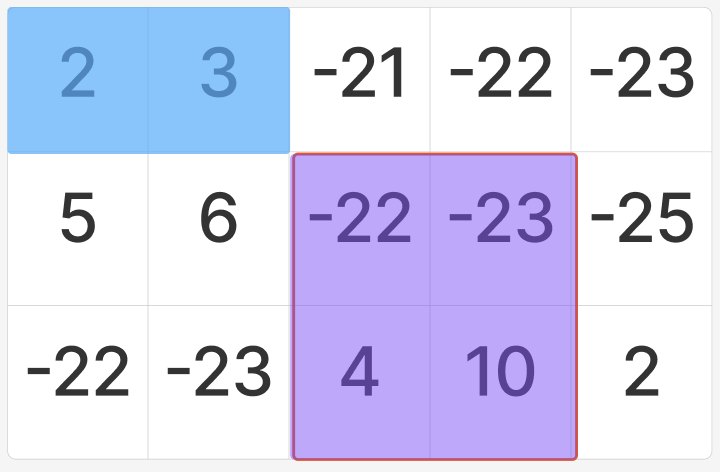
그런데 위 사진에서 파란색으로 칠해진 부분, 즉 (1, 1)에서 (1, 2)까지의 합은 둘이 겹쳐져 있던 부분이라 뺄셈이 중복으로 이루어졌다. 그러므로 현재까지의 계산 결과에서 이 부분을 한 번 더해준다.

색상이 겹쳐 잘 구분은 안 가지만, 한 번에 정리하면 위 사진과 같다.
(1, 1)부터 임의의 모든 위치까지의 합이 구해진 상태일 때,
(전체 - 왼쪽 빨간색 - 위쪽 빨간색 + 빨간색이 겹치는 부분)
이런 식으로 부분 행렬의 합을 구할 수가 있는 것이다.
이걸 일반화해서 (i, j)에서 (p, q)까지의 부분행렬의 합을 구하는 식을 세우면
sum[p][q] - sum[p][j - 1] - sum[i - 1][q] + sum[i - 1][j - 1]
와 같은 형태가 된다.
이런 식으로 이차원 배열의 누적합을 구해서 활용하는 방식을 이전에도 본 적이 있다고 스터디원분께서 그러셨다. 간혹 나오는 접근법인 것 같으니 기억해두면 좋을 것 같다.
구현
그런데 여기까지 어찌 저찌 생각은 했는데, 구현을 하려면 (i, j)부터 (p, q)까지의 부분 행렬 합을 모두 구해서 최댓값을 찾아야 하는데 좌표 값이 총 4개이다보니 4차원 메모이제이션 배열이나 4중 for문이 불가피할 거 같아서 이게 맞나? 하는 생각을 했다.
그래서 결국 풀이를 찾아봤는데, 진짜 그게 맞더라,,,, 말 그대로 브루트포스였다.
import java.io.*;
import java.util.*;
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int[][] sum = new int[N + 1][M + 1];
// (1, 1)에서 (i, j)까지의 누적합 구하기
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= M; j++) {
int num = Integer.parseInt(st.nextToken());
sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + num;
}
}
// (i, j)에서 (p, q)까지의 부분행렬의 합 구하기 -> 그 중에서 최댓값 찾기
int result = sum[1][1];
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
for (int p = i; p <= N; p++) {
for (int q = j; q <= M; q++) {
result = Math.max(result, sum[p][q] - sum[p][j - 1] - sum[i - 1][q] + sum[i - 1][j - 1]);
}
}
}
}
System.out.println(result);
}
}
흥미로운 문제였다....ㅋㅋㅋ
