프로그래머스 Lv2 N개의 최소공배수

문제

링크

풀이

python

def gcd(a, b) :
    max_num = max(a, b)
    min_num = min(a, b)
    while max_num % min_num != 0 :
        num = max_num % min_num
        max_num = min_num
        min_num = num
    return min_num

def solution(arr):
    answer = arr[0]
    for i in range(1, len(arr)) :
        number = gcd(answer, arr[i])
        answer = answer * arr[i] // number
    return answer

javascript

function gcd(a, b) {
    // a >= b
    if (a % b === 0) {
        return b;
    }
    return gcd(Math.max(a%b, b), Math.min(a%b, b));
}

function solution(arr) {
    let numA = arr[0];
    for (let i=1; i<arr.length; i++) {
        let numB = arr[i];
        let numGcd = gcd(Math.max(numA, numB), Math.min(numA, numB));
        numA = numA * numB / numGcd;
    }
    return numA;
}

유클리드 호제법에 대해 아시나요..?
이 문제는 유클리드 호제법을 알고 있다면??? 정말 쉽게 풀 수 있다.
이제부터 최소공배수, 최대공약수 문제는 무조건 유클리드 호제법 !!!!!!!!!!!!!!

유클리드 호제법을 간단하게 설명하자면, 두 수의 최대 공약수를 구하는 방법이다.

14와 63의 최대 공약수를 구해보자.
까마득한 옛날에 배웠던 방식으로 풀면 아래와 같이 풀 수 있다.

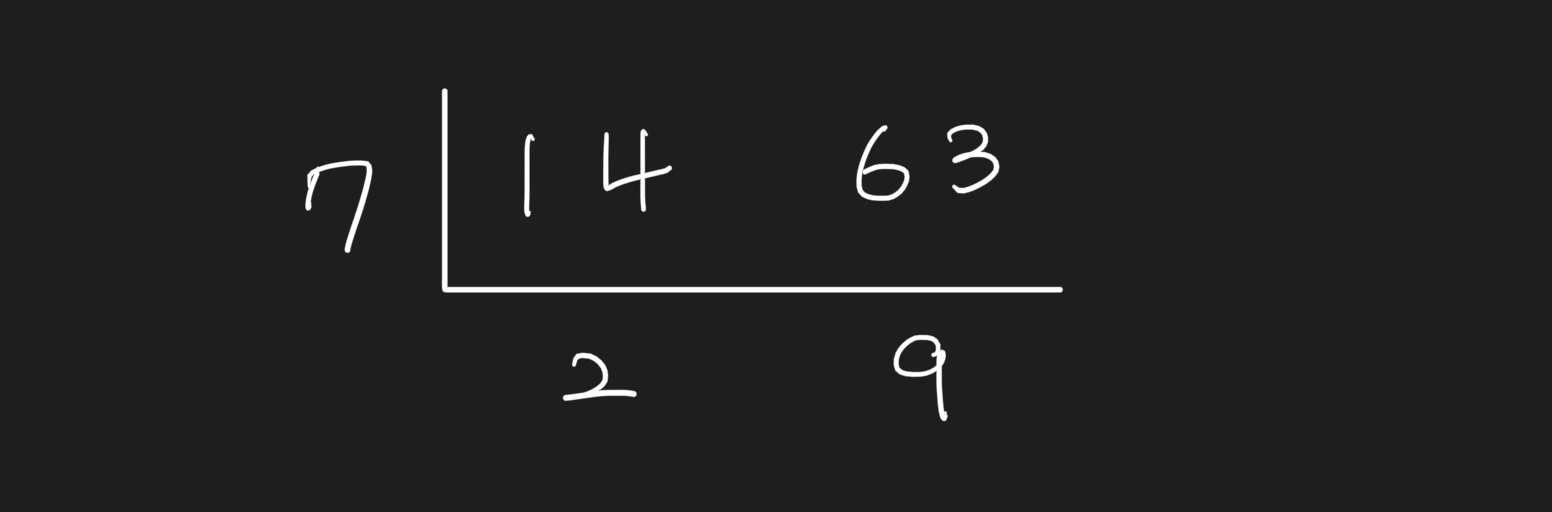
혹은 각 수를 엄청 나눠서 소수의 n제곱 형태로 만들어서 구할 수 있다.
하지만.. 이런 방법을 어떻게 코드로 나타낼 지 감이 안왔다. (그래서 다른 분들의 코드를 참고했다)

그렇다면 유클리드 호제법을 이용하면 어떻게 풀 수 있을까?

유클리드 호제법

1. 큰 수를 작은 수로 나누기.
2. 나머지가 있을 경우, 그 나머지와 1번에서 나눴던 작은 수의 크기를 또 비교해서 큰 수를 작은 수로 나누기.
3. 나머지가 없을 경우 나눴던 작은 수가 바로 최대공약수다!

말로 표현하니까 애매하므로 직접 수를 대입해서 풀어보자.

1. 큰 수를 작은 수로 나누기
   14, 63의 최대 공약수를 구해보자.
   먼저 14 < 63 이므로 63을 14로 나눠보자.
   $63 / 14 = 4$, 나머지 : 7
2. 나머지가 있을 경우, 그 나머지와 1번에서 나눴던 작은 수의 크기를 또 비교해서 큰 수를 작은 수로 나누기.
   1번에서 나눴던 작은 수 : 14
   나머지 : 7
   $14 / 7 = 2$, 나머지 : 0
3. 나머지가 없을 경우 나눴던 작은 수가 바로 최대공약수다!
   2번에서 나머지가 0이 나왔으므로, 나눴던 수인 7이 바로 최대공약수가 된다.

위와 같이 최대공약수를 구하는 방법이 바로 유클리드 호제법이다.

문제에서는 최소공배수를 요구하는데 유클리드 호제법을 적용해서 어떻게 풀 수 있을까?
아주 간단하다.

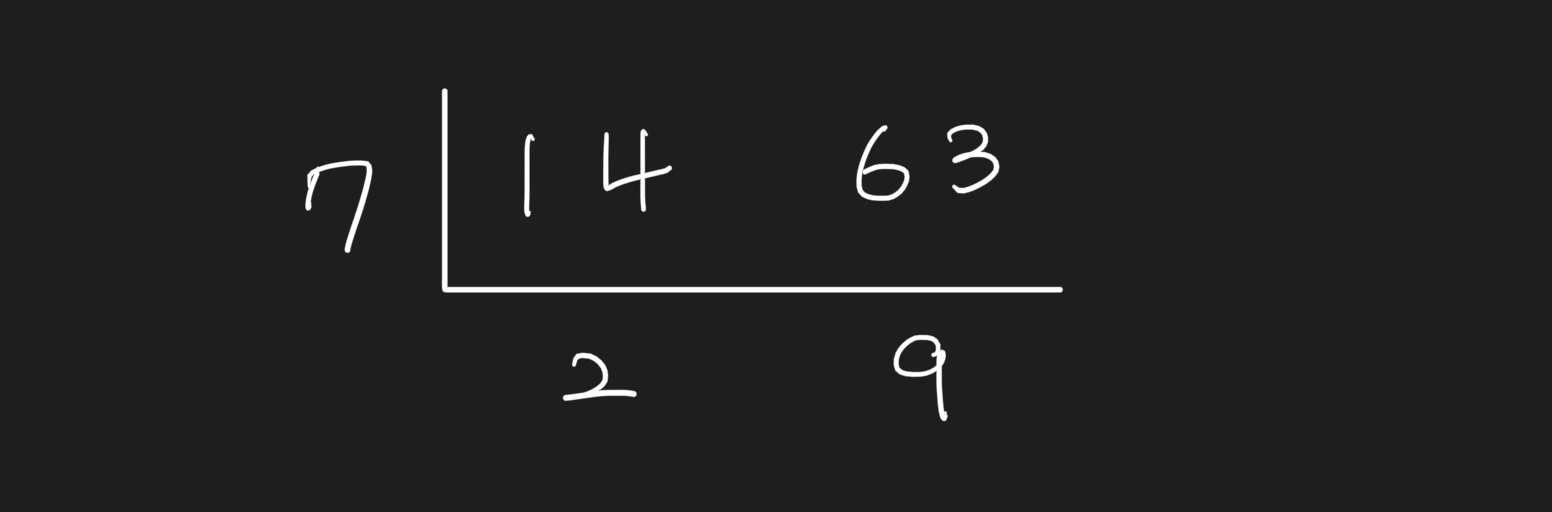
여기서 최대공약수는 7이고, 최소공배수는 $7*2*9$ 이다.
$14 * 63 = 7 * 2 * 7 * 9$
$14 * 63 = 최대공약수 * 최소공배수$ 라는 것을 알 수 있다!
그러므로 유클리드 호제법으로 알아낸 최대공약수를 이용해서 아래와 같이 최소공배수를 구할 수 있다.

최소공배수 = (비교하는 두 수의 곱) / 최대공약수

[a, b, c, d] 이렇게 수가 두 개 이상이라면 a, b의 최소공배수를 먼저 구하고, 앞서 구한 최소공배수와 c의 최소공배수를 구하고, 또 앞서 구한 최소공배수와 d의 최소공배수를 구하면 된다.