피보나치의 수열(Fibonacci Sequence)

References

아래 링크의 강의 중 Section 16. Runtime Complexity in Practice - Fibonacci의 내용을 추려 이번 글을 작성하였습니다.
The Coding Interview Bootcamp: Algorithms + Data Structures on Udemy

Solution 1. for loop

function fib(n) {
  const result = [0, 1];

  for (let i = 2; i <= n; ++i) {
    const a = result[i - 2];
    const b = result[i - 1];

    result.push(a + b);
  }

  return result[n];
}

console.log(fib(9));

function iteratingFib(n) {
  if (n <= 1) return n;

  let twoBehind = 0;
  let oneBehind = 1;
  let result = 0;
  for (let i = 1; i < n; ++i) {
    result = twoBehind + oneBehind;
    twoBehind = oneBehind;
    oneBehind = result;
  }
  return result;
}

console.log(iteratingFib(9));

for문을 돌면서 배열 result내의 index를 활용해 앞의 수 b와 앞앞의 수 a를 더해서 배열 result에 push한다. 결과값으로 배열 result 내 입력값 n번째에 있는 값을 반환한다.
첫 번째 함수에서 유의할 점 0, 1을 배열 result에 미리 설정해둔다는 점이다.

Solution 2. recursive function

function fib(n) {
  if (n === 0) return 0;
  else if (n === 1) return 1;
  else return fib(n - 1) + fib(n - 2);
}

console.log(fib(9));

function fib(n) {
  if (n < 2) {
    return n;
  }

  return fib(n - 1) + fib(n - 2);
}

console.log(fib(9));

위 두 코드 모두 재귀함수를 통해 피보나치 수열을 구하는 공식이다. 입력값 n이 0 혹은 1일 경우 더할 값이 없으므로 그대로 n을 반환하고, 아닐 경우 재귀함수를 돌면서 앞의 수와 앞앞의 수를 더해나간다. 밑의 도표와 같이 작동한다.

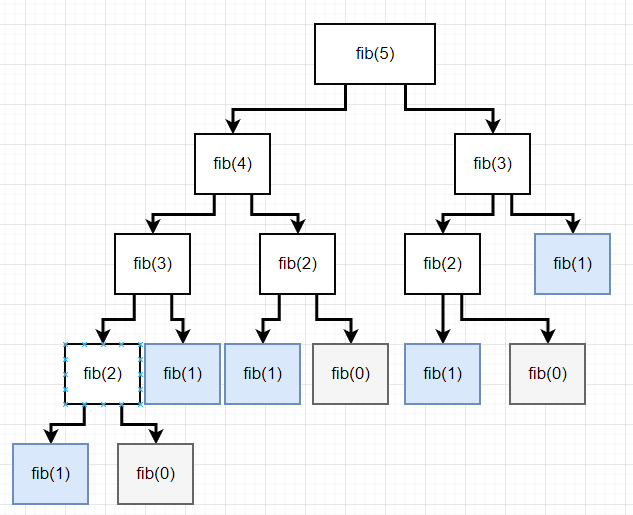
n으로 5를 입력했을 경우 return fib(n - 1) + fib(n - 2)를 반복하면 결과적으로 fib(1)은 5개가 남는다. 이 값을 모두 더해서 반환하는 것이다.