백준 / 1028 / 다이아몬드 광산 / python

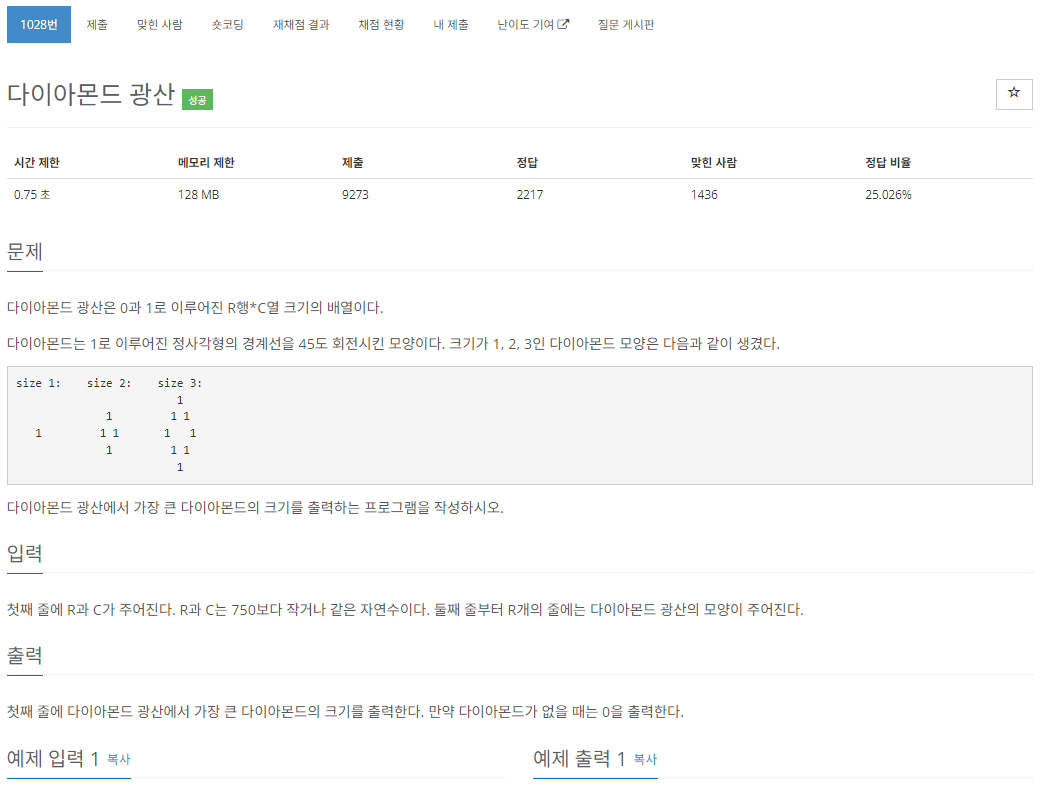
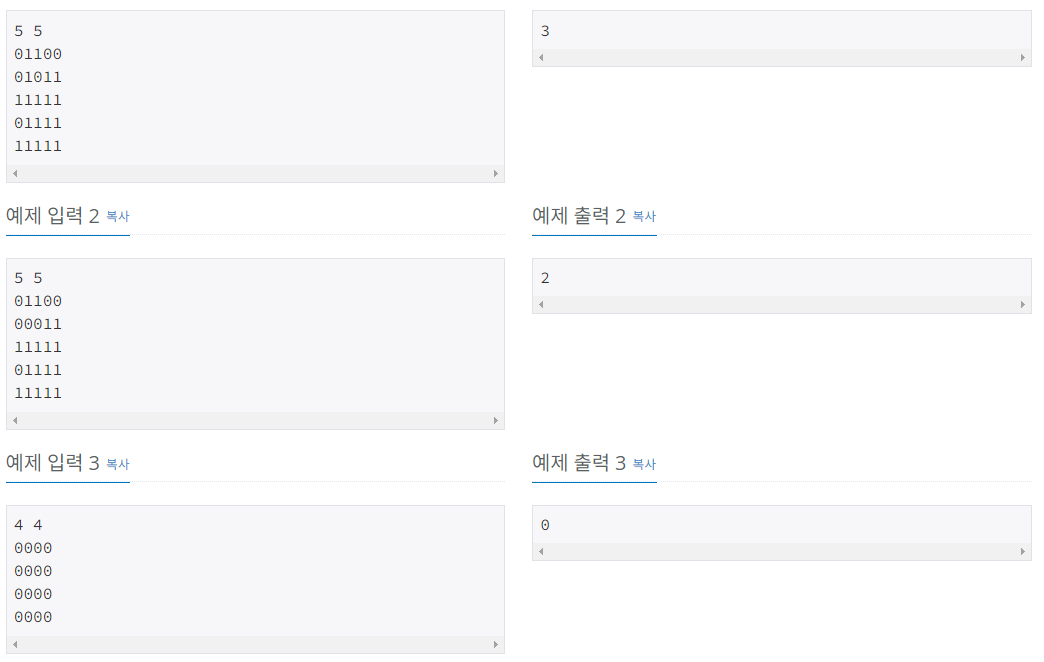
첫 시도 코드

r, c = map(int, input().split())

def check(x,y, k):
    cnt = 0
    for i in range(-k, k+1):
        nx, ny1, ny2 = x+i, y - cnt, y + cnt
        if not(0 <= nx < r and 0 <= ny1 < c and 0 <= ny2 < c):
            return False
        if mount[nx][ny1] and mount[nx][ny2] and 1:
            if i >= 0:
                cnt -= 1
            else:
                cnt += 1
            continue
        else:
            return False
    return True

mount = [[0]* c for _ in range(r)]
for i in range(r):
    s = input()
    for j in range(c):
        mount[i][j] = int(s[j])

result = 0
for i in range(r):
    for j in range(c):
        # 다이아 확인
        for k in range(result, 750//2 + 1):
            if check(i,j,k):
                result = k+1

print(result)

완전 탐색 방식으로 시도 이중 for문을 돌면서 해당 좌표에서 1크기의 다이아 부터 최대 750 크기의 다이아를 계속 확인 하는 방법
시간복잡도를 생각해보면 n^3으로 판단된다. 시간 초과가 발생한다.

dp를 사용한 방법

n, m = map(int, input().split())
board = [[0] * (m+2) for _ in range(n+2)]

for i in range(1,n+1):
    s = input()
    for j in range(1,m+1):
        board[i][j] = int(s[j-1])

ld = [[0] * (m+2) for _ in range(n+2)]
rd = [[0] * (m+2) for _ in range(n+2)]
lu = [[0] * (m+2) for _ in range(n+2)]
ru = [[0] * (m+2) for _ in range(n+2)]

for i in range(n, 0, -1):
    for j in range(1, m+1):
        if board[i][j] == 1:
            ld[i][j] = ld[i+1][j-1] + 1
            rd[i][j] = rd[i+1][j+1] + 1

for i in range(1, n+1):
    for j in range(1, m+1):
        if board[i][j] == 1:
            lu[i][j] = lu[i-1][j-1] + 1
            ru[i][j] = ru[i-1][j+1] + 1

result = 0
for i in range(1, n+1):
    for j in range(1, m+1):
        l = result if result != 0 else 1
        for k in range(l, min(ld[i][j], rd[i][j])+1):
            t = i + (k-1)*2
            if t > n+1:
                break
            if board[t][j] and lu[t][j] >= k and ru[t][j] >=k:
                result = k
        for k in range(l, min(rd[i][j], ru[i][j])+1):
            t = j + (k-1)*2
            if t > m+1:
                break
            if board[i][t] and lu[i][t] >= k and ld[i][t] >=k:
                result = k
print(result)

우선 대각선에 대한 누적 합을 저장한다.
왼쪽 아래 방향, 위 방향. 오른쪽 아래 방향, 위 방향.
이렇게 4개를 저장한다.

ld[i] = 왼쪽 아래로 이어져 있는 1의 개수,
rd[i] = 오른쪽 아래로 이어져 있는 1의 개수,
lu[i] = 왼쪽 위로 이어져 있는 1의 개수,
ru[i] = 오른쪽 위로 이어져 있는 1의 개수.
이는 주어진 맵을 스캔하는 과정에서 O(N^2) 에 전체 DP table을 채울 수 있다.

저장한 다음 2중 for 문을 돌면서 왼쪽 위에서 시작하는 마름모, 오른 쪽에서 시작하는 마름모로 구할 수 있다.