백준 / 1644 / 소수의 연속합 / python

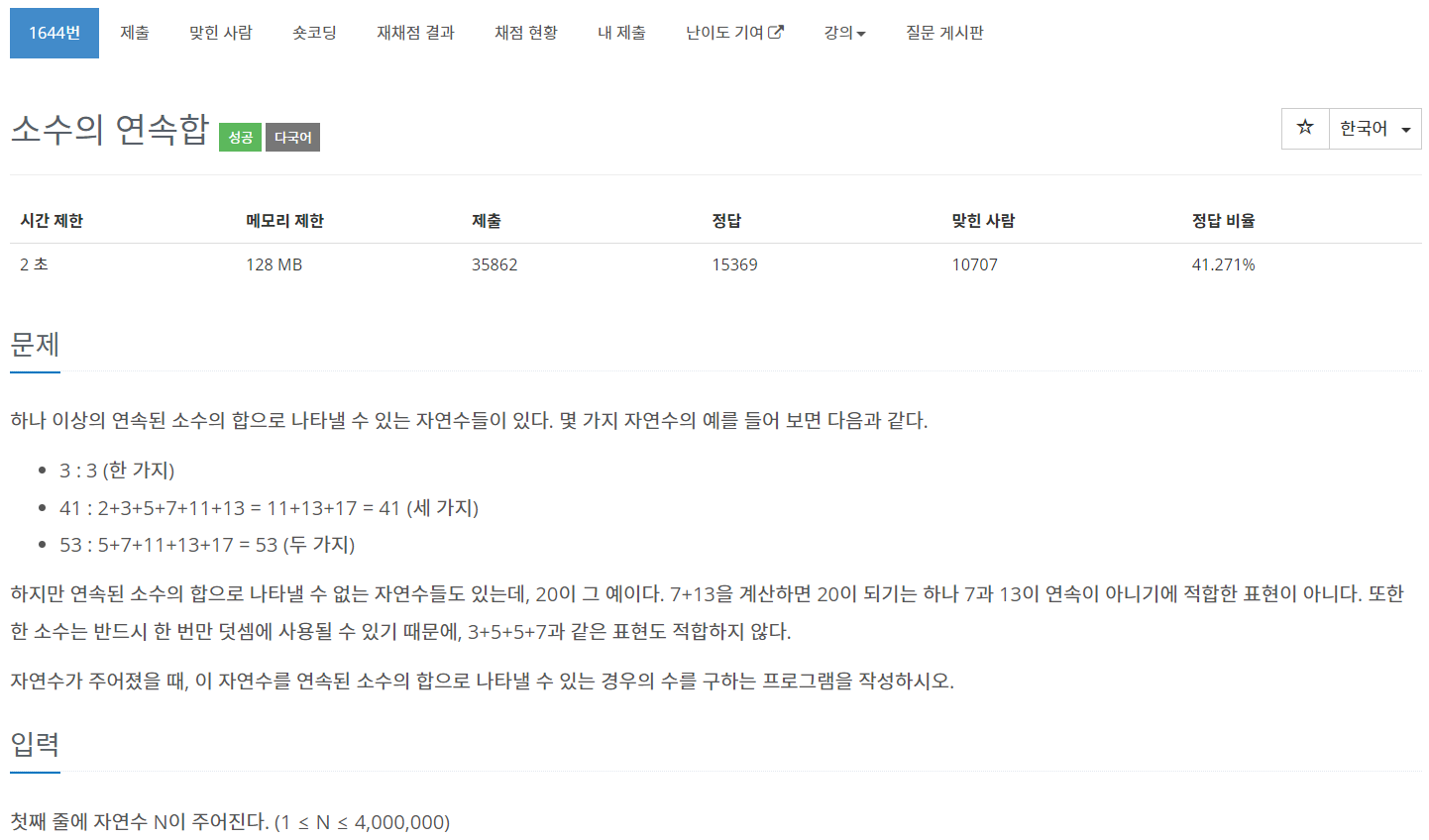
import math

n = int(input())

l = [True] * (n+1) # 0,1을 제외한 모든 숫자가 소수(True)인 것으로 설정하고 시작한다.

# 에라토스테네스의 체 알고리즘
for i in range(2, int(math.sqrt(n)) + 1): # 2부터 n의 제곱근까지의 모든 수를 확인
    if l[i] == True: # i가 소수인 경우 i를 제외한 i 배수 모두 지우기
        j = 2
        while i * j <= n:
            l[i * j] = False
            j += 1

sosu = [0]
for i in range(2, n+1):
    if l[i]:
        sosu.append(i)

for i in range(1, len(sosu)):
    sosu[i] += sosu[i-1]

left, right = 0, 1

cnt = 0
while right < len(sosu):
    tmp = sosu[right] - sosu[left]

    if tmp == n:
        cnt += 1
        left += 1
    elif tmp < n:
        right += 1
    else:
        left += 1

print(cnt)

소수 구하는 방법은 에라토스테네스의 체 알고리즘으로
소수가 되는 경우를 찾는 거은 누적합과 투 포인터 알고리즘으로 해결했다.

오랜만에 보는 "애라토스테네스의 체 알고리즘"
n 크기의 true 배열을 만들고 소수인 경우는 true로 두고 해당 소수의 배수를 모두 False로 만들어 나가는 방식으로 소수를 구하는 알고리즘

12를 생각해볼때 2 x 6, 3 x 4나 4 x 3, 6 x 2는 같은 경우이기 때문에
해당 숫자 까지의 소수를 구할때는 해당 숫자의 제곱근 까지로 구해서 연산량을 줄일 수 있다.