프로그래머스 / 디스크 컨트롤러 / python

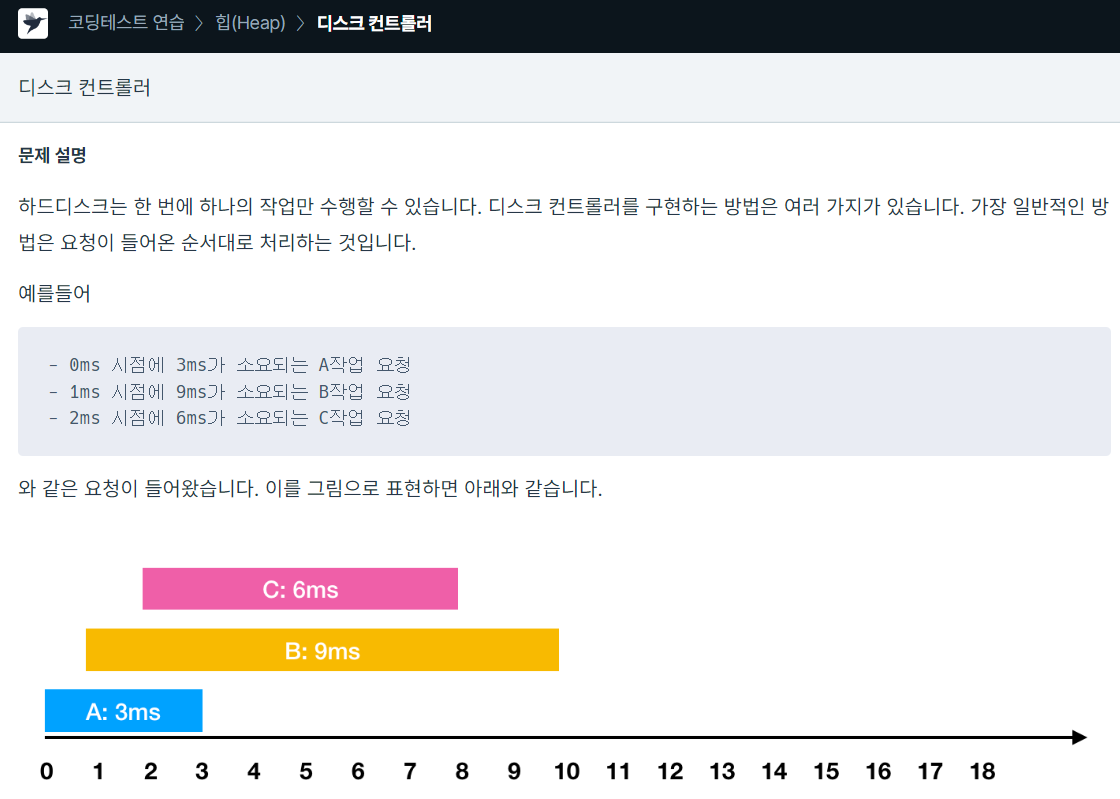
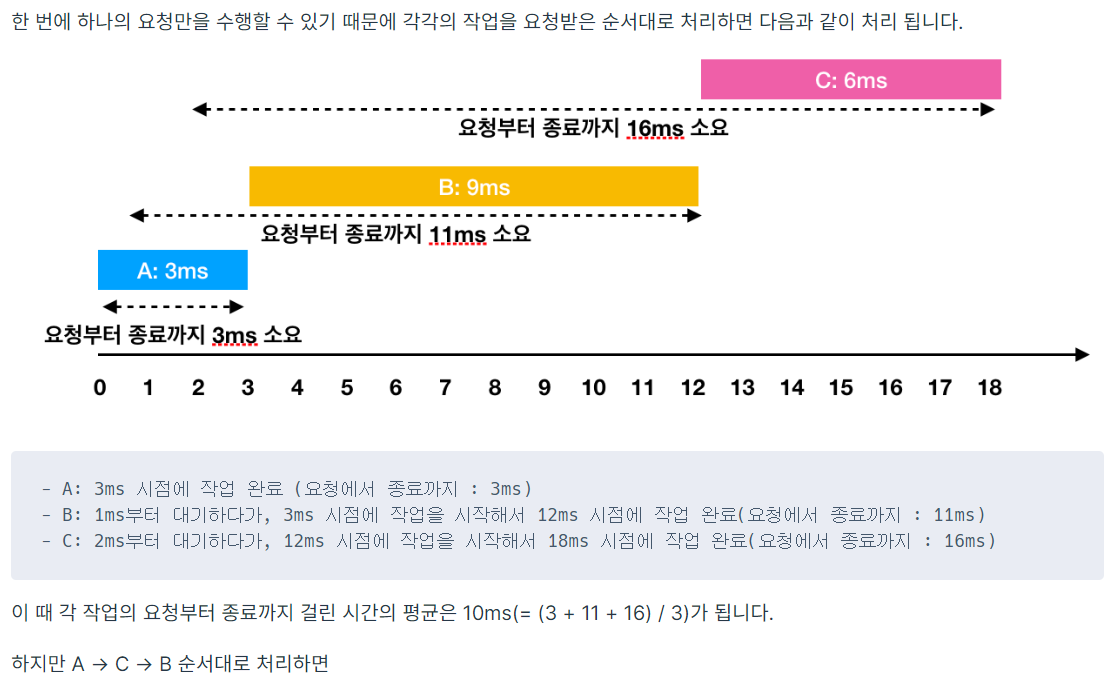
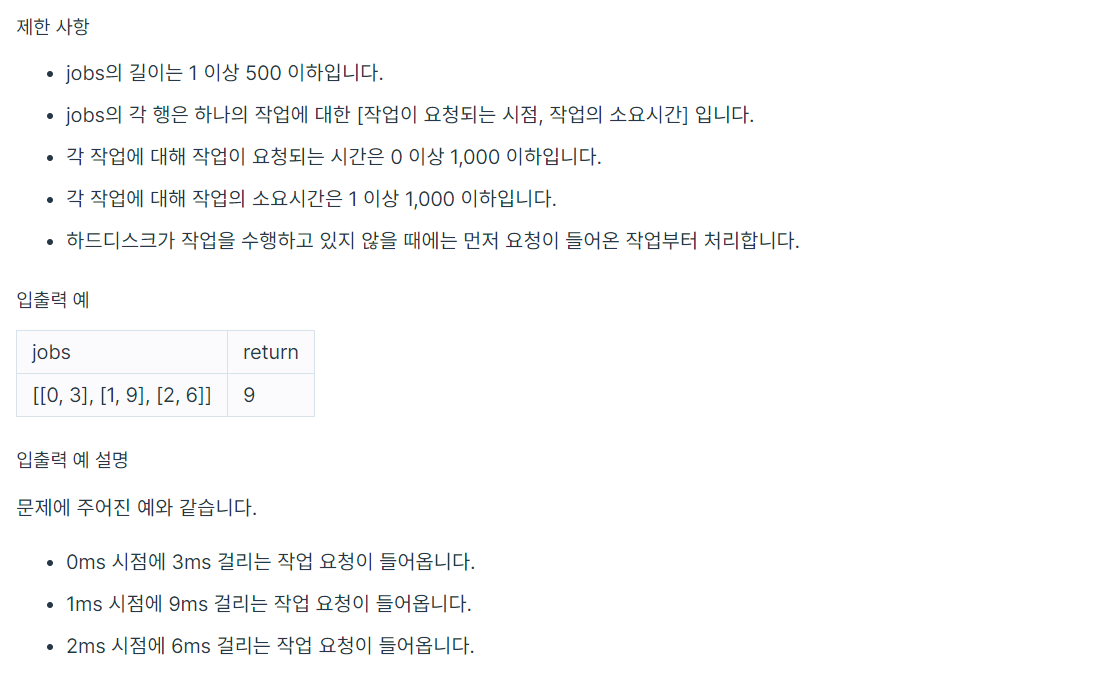
from heapq import heappop, heappush

def solution(jobs):
    answer = []
    idx = 1
    jobs.sort(key=lambda x:[x[0], x[1]])
    
    h = [(jobs[0][1], jobs[0][0])]
    now = jobs[0][0]
    while h:
        # print(h)
        e, s = heappop(h)
        answer.append(now-s+e)
        now += e
        # print(now)
        while idx < len(jobs) and now > jobs[idx][0]:
            heappush(h, (jobs[idx][1], jobs[idx][0]))
            idx += 1
        if not h and idx < len(jobs):
            heappush(h, (jobs[idx][1], jobs[idx][0]))
            now = h[0][1]
            idx += 1
    # print(answer)
    return sum(answer) // len(jobs)

heap을 사용해서 해결하는 문제
우선 jobs를 요청시간으로 정렬하는데 최소 시간을 구하기 위해서는 같은 요청시간에 대해서 소요시간 정렬도 필요하다.

그 다음 now 변수를 통해서 종료시간을 계속해서 누적 저장하며 answer에는 now - start + end을 저장하는데
의미를 살펴보자면 현재 시간에서 요청시간 을 뺌으로써 얼만큼 기다렸는지를 구하고 소요시간을 구해서 총 요청시간으로 부터 최종적으로 처리된? 끝난 시간을 구할 수 있다.

jobs가 정렬 되어있으므로 now보다 작은 요청시간 즉 현재 디스크가 끝나는 시간보다 요청시간이 작은 job은 heap에 저장한다. heap에 저장할때는 소요시간을 첫 번째로 오게해서 소요시간으로 정렬되게 해야한다.

heap이 비어있지만 job을 모두 탐색한게 아니라면 heap에 다음 job을 추가해주고 현재시간을 해당 job의 시작시간으로 바꿔주면 된다.