프로그래머스 / 섬 연결하기 / python

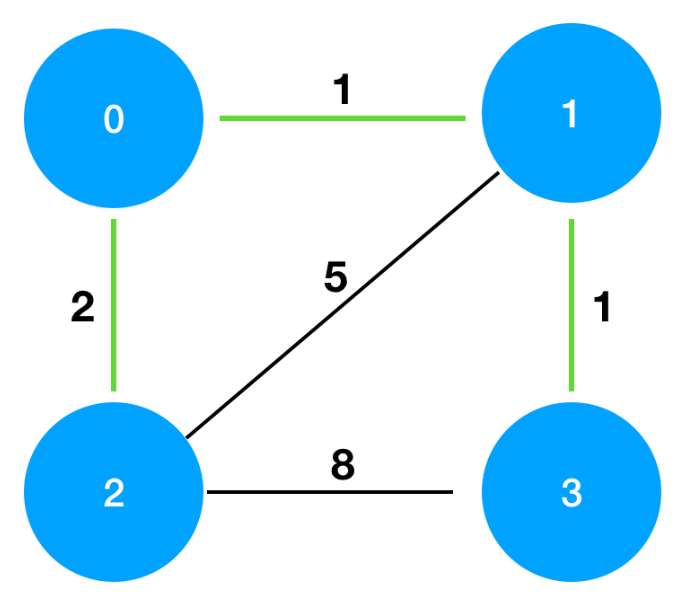
다른 분들이 많이 사용한 Kruskal 알고리즘

def solution(n, costs):
    answer = 0
    costs.sort(key = lambda x: x[2])
    link = set([costs[0][0]])
    
    while len(link) < n:
        for cost in costs:
            if cost[0] in link and cost[1] in link:
                continue
            if cost[0] in link or cost[1] in link:
                answer += cost[2]
                link.update([cost[0], cost[1]])
                break

    return answer

Kruskal 알고리즘을 알고나면 어렵지 않게 풀 수 있는 문제이다.
알고리즘 자체도 이해하기 쉬운 편이였다. 하지만 처음 떠올린 다익스트라 알고리즘으로 풀고 싶었다.

from heapq import heappush, heappop

def solution(n, costs):
    answer = 0
    
    graph = [[] for _ in range(n)]
    for cost in costs:
        graph[cost[0]].append((cost[1], cost[2]))
        graph[cost[1]].append((cost[0], cost[2]))
        
    h = [(0,0)]
    visited = [False] * n
    
    while h:
        c, node = heappop(h)
        
        if visited[node]:
            continue
        visited[node] = True
        
        answer += c
        
        for next_node, next_c in graph[node]:
            if not visited[next_node]:
                heappush(h, [next_c, next_node])
    
    return answer

다익스트라 알고리즘으로 해결한 코드
기본적인 다익스트라와 다른 점은 시작점에서의 거리를 누적?해서 저장하지 않고 graph를 순환하며서 해당 간선의 크기만 저장한다.