프로그래머스 / 숫자 변환하기

from collections import deque

def solution(x, y, n):
    answer = 0
    q = deque([x])
    visited = [0] * (y+1)
    while q:
        t = q.popleft()
        
        if t == y:
            return visited[t]
        for i in [t*2, t*3, t+n]:
            if i <= y and not visited[i]:
                visited[i] = visited[t] +1
                q.append(i)
           
    return -1

이 문제를 해결하는 방법으로 크게 두가지를 떠올릴 수 있다. Dp와 bfs
위 코드는 bfs로 푼 방법이다.

def solution(x, y, n):
    answer = 0
    dp = [10e9] * (y+1)
    dp[x] = 0
    for i in range(x,y+1):
        for j in [i*2, i*3, i+n]:
            if j < y+1 and dp[i] != 10e9:
                dp[j]= min(dp[i]+1, dp[j])
    
    return dp[y] if dp[y] != 10e9 else -1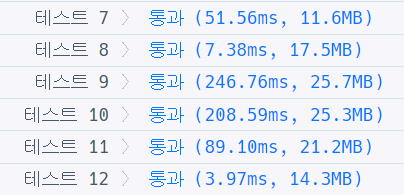

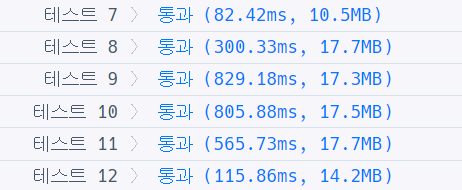
위 이미즌 bfs 방식으로 제출한 것이고 아래 이미지는 DP 알고리즘으로 제출한 것이다.

생각해보면 이 문제는 최단 경로를 구하는 것이고 이런 경우에는 y 값까지 도달하기 전까지 모든 수를 확인하는 Dp 방식보단 bfs가 더 효율적이다.

---

어떤 알고리즘이 더 효율적인지도 생각해야 한다는 걸 깨닫게 해 준 문제이다.