프로그래머스 / 연속된 부분 수열의 합 / python

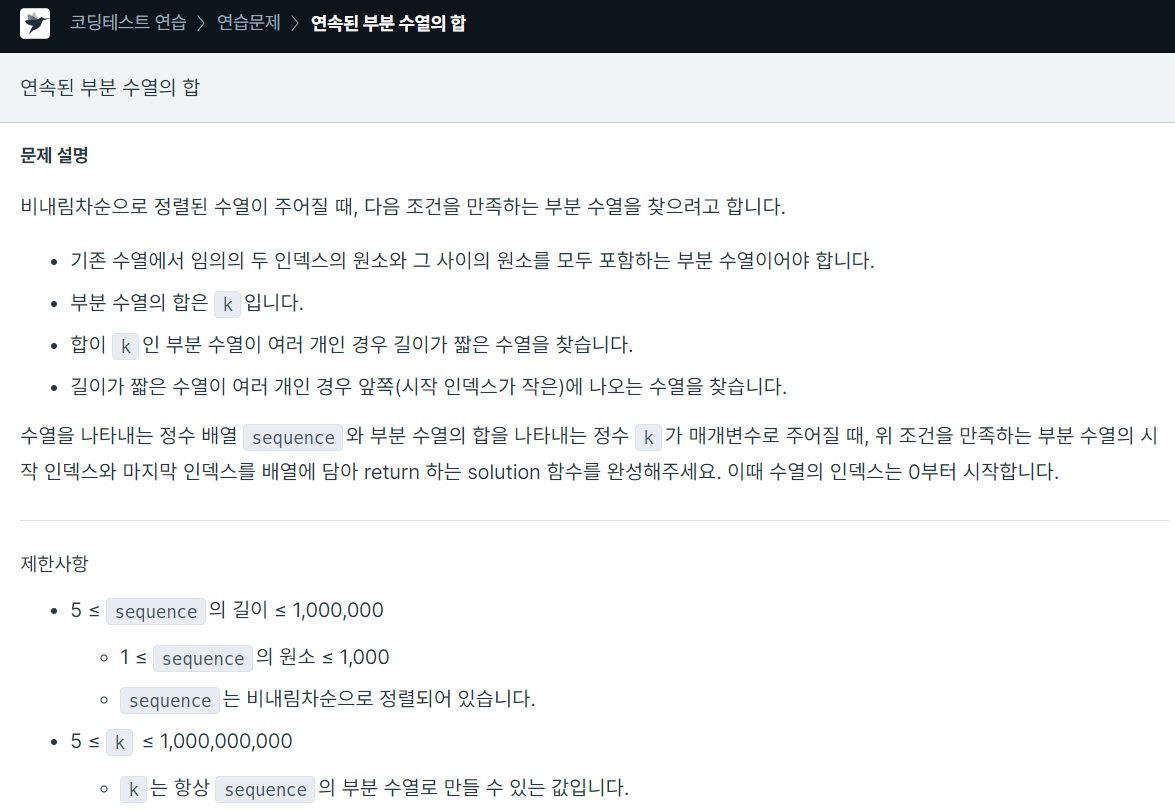
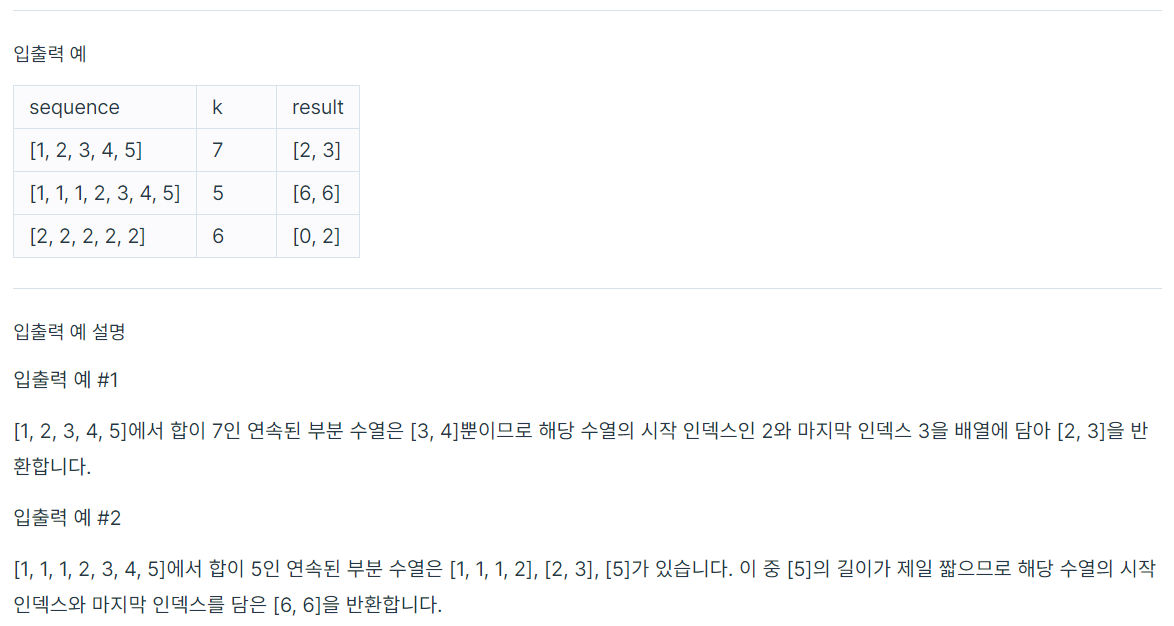
처음 시도한 방법

def solution(sequence, k):
    answer = []
    if k in sequence:
        return [sequence.index(k), sequence.index(k)]
    
    s = [0] * len(sequence)
    s[0] = sequence[0]
    for i in range(1, len(sequence)):
        s[i] = s[i-1] + sequence[i]

    result = []
    for i in range(len(s)):
        if s[i] > k:
            for j in range(i):
                if s[i] - s[j] == k:
                    result.append([j+1, i, i-j])
                    
        if s[i] == k:
            result.append([0, i, i])
    
    answer = min(result, key= lambda x: x[2])[:2]
    return answer

누적 합을 통해 처음에 시도했다.
누적 합이기 때문에 시간 복잡도가 O(nlong)라고 생각해 충분히 풀 수 있다고 판단했지만 히든 케이스에서 많은 케이스가 시간 초과가 나왔다.

누적합을 사용했지만 2중 for문 조건을 보면 누적 합에서 k 보다 큰 경우일 때 인덱스 0 부터 현재 인덱스까지 탐색한다.

근데 누접 합이기 때문에 현재 인덱스의 누적합 값이 k 보타 크기 사작하면 계속해서 0부터 현재 인덱스까지 탐색한다. 즉 위 코드는 O(n^2)이다....

결국 혼자 해결하진 못했고 인터넷을 통해 two point를 사용하면 된다는 것을 알았다.

def solution(sequence, k):
    answer = [0,len(sequence)]
    left = right = 0
    
    tmp = 0
    while right < len(sequence):
        tmp += sequence[right]
        if tmp <= k:
            right += 1
        else:
            tmp -= sequence[right]
            tmp -= sequence[left]
            left += 1
            
        if tmp == k and right-1 - left < answer[1] - answer[0]:
            answer = [left, right-1]
            
    return answer

투 포인터 알고리즘으로 해결

tmp를 통해 left, right 두 포인트 사이 값들의 합을 저장한다. tmp 값이 주어진 k 보다 작다면 더 더해야 하므로 right를 증가시킨다.

k값보다 크다면 left 값을 감소 시키면서 값을 다시 감소 시켜주다.