더 이상 배열의 탐색비용은 O(n)이 아니다, 이진탐색(Binary Search)

배열의 탐색은 기본적으로 시간복잡도가 O(n)이다. 특정값을 찾기 위해서는 최선의 경우 바로 찾던 값이 배열의 맨 앞에 있을 수 있지만, 그렇지 않은 경우 배열의 길이n만큼 하나 씩 값이 맞는지 대조하기 때문이다. 하지만, 정렬이 O(n2)으로 연산되던 것을 O(n log n)의 비용으로 가능했던 것처럼, 탐색 역시 O(n)에서 O(log n)으로 줄일 수 있다.

이진탐색트리와 이진탐색

이진탐색을 알아보기에 앞서 이진탐색트리를 떠올려보자. 이진탐색트리는 저장할 값들을 순서를 정해서 저장한 이진트리다. 루트 값으로 선택한 부모를 기준으로, 작은 값은 left 포인터에 큰 값은 right에 저장하며, 자식 노드가 있는 경우는 자식 노드와 비교하여 마찬가지로 left와 right 포인터에 저장하는 구조다.

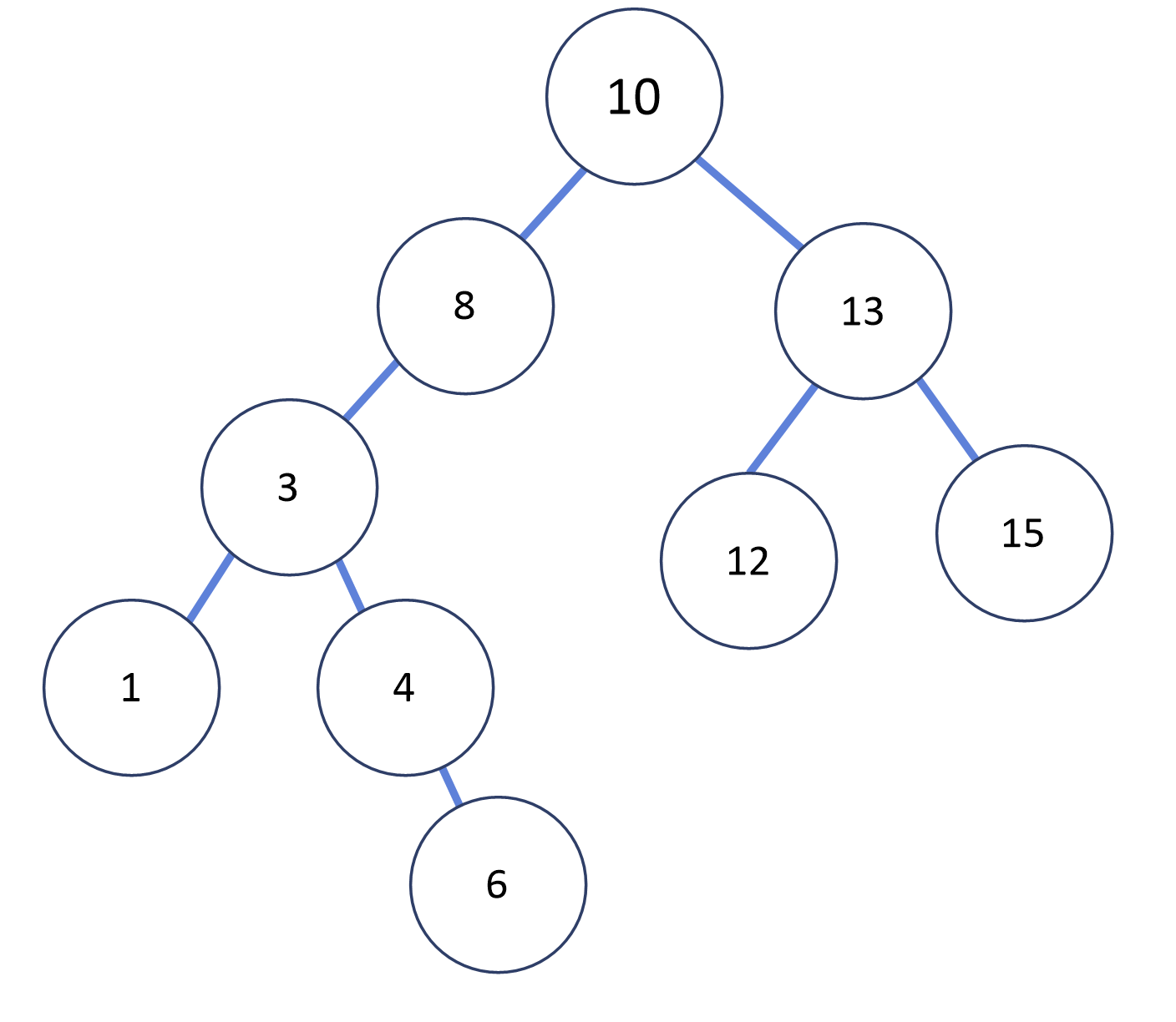
이진 탐색트리는 높이가 h일 때, 원하는 값을 탐색하는 비용이 h이다. h번 만큼, 원하는 값보다 큰지 작은지 확인하면 되기 때문이다. 그렇다면 원소의 n일때 높이는 몇이 될까. 그것은 어떤 배열에서 어떤 루트 값을 가져오느냐에 따라 다르다.

만약 모든 노드가 left 포인터에는 아무 값도 가리키지 않고, right 포인터에만 자식 노드를 가리킨다면 h = n이 될 것이다. 이 때 이진탐색트리는 정렬된 배열과 다를 바 없으며, 탐색비용도 O(n)이다.

그러나 가장 효율적인 이진탐색트리를 구성하면, 요소가 하나일 때 1층, 셋일 때까지 2층, 일곱일 대가지 3층, ... 즉 2h-1개일 때 까지는 h층이 된다. n은 2와 h에 대한 등비수열의 합이므로 높이 h는 log2(N+1)-1을 소수점 첫째 자리에서 반올힘 한 값이 된다. 높이 값에 의해 탐색 비용도 log2(n+1)-1이고 시간복잡도는 O(logn)이 된다.

그렇다면 이진탐색은 어떨까. 이름의 유사성에서도 알 수 있듯이 이진탐색은 마치 최선의 이진탐색트리를 구성하는 것처럼 정렬된 배열을 가지고 매 연산마다 가운데 값을 타겟값과 비교하는 방법이다. 정확히는 가운데 값과 타겟을 비교하여 타겟값이 더 크면 큰 값들을, 작으면 더 작은 값들을 불러와 다시 비교하는 연산이다. 사실 타겟과 비교하는 가운데 값을 루트로 설정해 큰 값은 오른쪽 포인터에, 작은 값은 왼쪽 포인터에 저장하는 것과 같다. 때문에 탐색의 시간복잡도는 O(logn)이다.

다만 이진탐색트리와 다른 것은 타겟이 포함될 가능성이 없는 값은 계산하지도 않는 것이다.

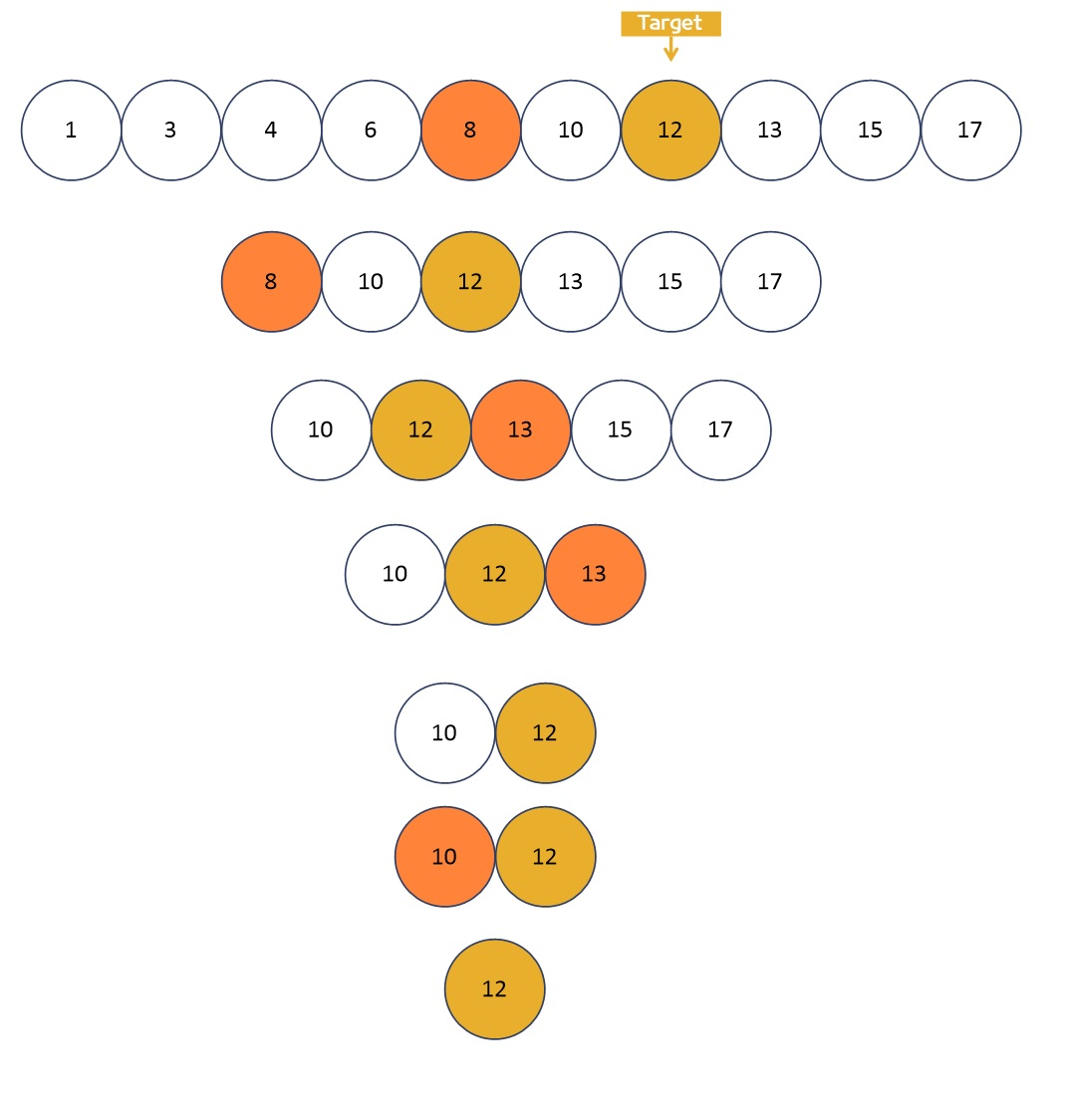
이진탐색구현

# 이진 탐색 함수 선언
def binary_search(nums, target):
    # 중첩 이진탐색 함수 선언
    def bs(start, end):
    	# 배열의 시작 인덱스를 가리키는 값이 끝 인덱스를 가리키는 값보다 커지 재귀 함수 종료
        # mid값이 target과 같은 경우 즉, 배열 안에 타겟이 없으면 -1 반환
        if start > end :
            return -1
        
        # mid에 중간 인덱스 값 저장
        mid = (start + end)//2
        
        # 중간 인덱스 값이 가리키는 값이 타겟보다 작으면
        if nums[mid] < target:
        	# 타겟보다 큰 값들을 배열로 중첩 이진탐색 함수 재귀호출
            return bs(mid + 1, end)
        
        # 중간 인덱스 값이 가리키는 값이 타겟보다 크면
        if nums[mid] > target:
            # 타겟보다 작은 값들을 배열로 중첩 이진탐색 함수 재귀호출
            return bs(start, mid-1)
            
        # 중간 인덱스 값이 타겟보다 크지도 작지도 않다면 == 타겟과 같다면
        # mid 반환
        else :
            return mid
    # 이진탐색함수의 인자 값인 nums의 시작, 끝 인덱스를 인자로 중첩함수 호출        
    return bs(0, len(nums)-1)

이진탐색의 구현 코드는 재귀와 함께 변하지 않는 값들(처음 배열, target)이 존재하므로 부모함수와 중첩함수의 형태로 구현하였다. 중첩함수는 부모의 인자값인 배열을 활용하여, 재귀호출 될 때마다 가상의 배열의 시작-끝 인덱스를 인자로 실행된다. 타겟 값이 있으면 타겟과 같은 값의 인덱스를, 없으면 -1을 반환한다.

# bisect 모듈 수령
import bisect

# 파이썬 내장모듈을 활용한 이진탐색함수 선언
# nums는 정렬된 배열
def binary_search_builtin(nums, target):

	# idx에 bisect모듈의 bisect_left 메서드의 결과값 저장
    # bisect_left는 배열과 타겟 값을 인자로 받음
    # 타겟 값이 있으면 해당 타겟의 인덱스를 반환
    # 타겟 값이 여러 개 있으면, 타겟과 같은 값 중 가장 왼쪽의 인덱스를 반환
    # 타겟 값이 없을 때, 타겟 값보다 큰 값이 있으면 해당 값의 인덱스를 반환
    # 타겟 값이 없을 때, 타겟 값 보다 큰 값이 없으면 배열의 길이를 반환
    idx = bisect.bisect_left(nums, target)
    
    # 결과값 idx가 배열 안의 인덱스 값이면서, 가리키는 값이 타겟과 같으면
    if idx < len(nums) and nums[idx] == target:
    	# idx 값 반환
        return idx
        
    # 같은 값이 없으면 -1 반환
    else :
        return -1

해당 구현 코드는 내장 모듈인 bisect를 활용한다. bisect의 내장함수 bisect_left는 이진탐색을 통해 타겟 값 혹은 타겟 값과 가장 가까운 큰 값을 탐색하여 해당 인덱스를 반환한다. 그리고 해당 인덱스가 없으면 배열 전체의 길이를 반환한다. 때문에 메서드의 결과 값이 타겟과 같은 값을 가리키는지 확인하여 반환하고, 타겟 값이 없으면 -1을 반환한다.

마무리

배열의 진화는 계속된다