배열은 찢어야 제 맛, 머지 정렬(Merge Sort)에서 이어집니다.
정렬 시리즈의 마지막은 힙 정렬이다. 힙 정렬은 J.W.J.윌리엄스가 자료구조 힙을 발명함과 동시에 탄생한 정렬 알고리즘이다. 힙을 활용하여 배열의 모든 요소를 입력하고, 차례로 꺼내 새로운 배열에 넣어서 정렬하는 알고리즘이다. 자료구조 힙에 대한 내용은 "우리 사장님들은 이거 보고 배우셔야 돼유, HEAP"에 적었지만 간단하게 얘기해보면, 배열을 완전이진트리의 관점에서 해석하여, 부모값과 자식값이 항상 조건에 부합하게 정렬하는 함수를 사용해 항상 최소 혹은 최대값을 반환하는 자료구조이다. 이를 활용한다면, 힙 정렬은 매우 손쉽게 이루어진다.
힙 정렬
최소 힙에 모든 요소를 담았다가, 힙의 요소들을 차례로 순회하며 값을 선입선출 형태로 넣으면 오름차순, 후입선출 형태로 넣으면 내림차순으로 정렬할 수 있다. 반대로 최대 힙에 모든 요소름 담았다가, 힙의 요소들을 차례로 순회하며 값을 선입선출 형태로 넣으면 내림차순, 후입선출 형태로 넣으면 오림차순으로 정렬된다.
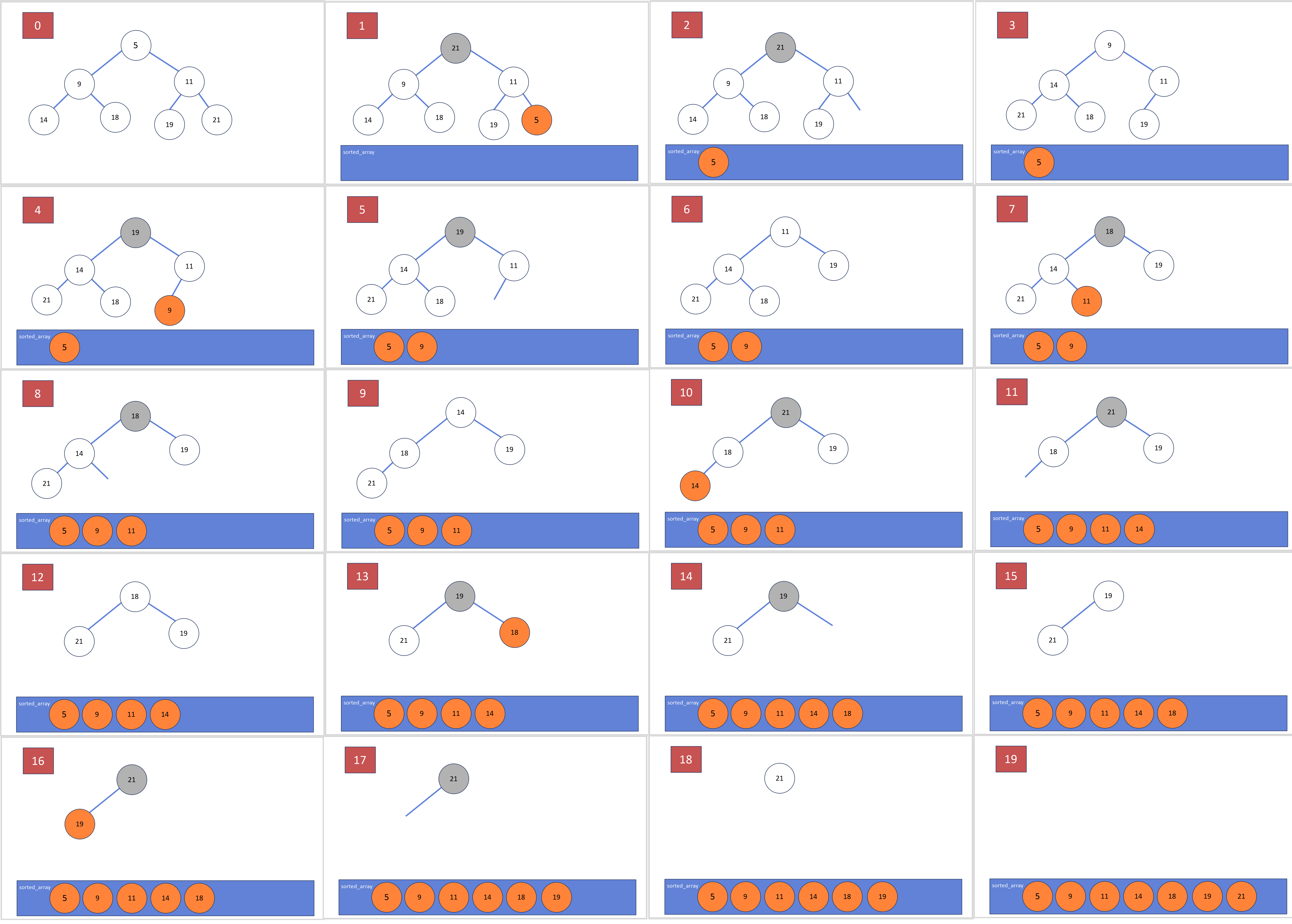
그림과 같이 매 루트에 있는 요소를 맨 끝의 요소와 교환하여 빼내고, 바뀐 루트의 요소를 재정렬하는 과정이 반복된다. 그림에서는 최소 힙을 활용하 오름차순으로 정렬했지만, 최대힙을 활용하는 경우 배열은 내림차순으로 정렬된다.
힙 정렬의 구현
힙 정렬을 파이썬으로 구현해보자. 최소 힙의 구현함수까지 같이 보자.
# 최소 힙 클래스 선언
class BinaryMinHeap:
# 힙 안의 저장 배열 선언, 인덱스 계산의 편의를 위해 0번째 인덱스는 None
def __init__(self):
self.items = [None]
# 길이 값 반환 매직매서드 선언, 저장 배열의 길이 값 -1을 반환한다.
# -1은 초기화할 때 넣은 None을 제외하기 위함
def __len__(self):
return len(self.items)-1
# 요소 상향 이동 함수
def _percolate_up(self):
# 현재 값은 가장 끝의 값으로 설정, 인덱스 값 저장
cur = len(self)
# 현재 값의 부모 인덱스 값 저장
# 0번째 인덱스 None을 제외하고 이진트리를 기준으로
# 1, 2(2,3), 4(4,5,6,7), 8(8,9,10,11,12,13,14,15) ... 단위로 배치되기 때문에
# 레벨 2의 부모 인덱스는 1
# 레벨 3의 부모 인덱스는 4,5의 경우 2/ 6,7의 경우 3
# 레벨 4의 부모 인덱스는 8,9의 경우 4/ 10,11의 경우 5 ... 이므로
# 부모의 인덱스 값은 cur//2 이다.
parent = cur//2
# 만약 부모의 인덱스가 0보다 크다면 반복
# 부모의 인덱스가 0이라는 것은, cur이 루트를 가리킨다는 의미
while parent > 0 :
# 현재 값이 부모 값보다 작다면
if self.items[cur] < self.items[parent] :
# 현재 값과 부모 값을 교환
self.items[cur], self.items[parent] = self.items[parent], self.items[cur]
# 반복문이 실행될 때 마다, 현재 값의 인덱스를 부모 인덱스로 갱신
cur = parent
# 부모 인덱스는 부모의 부모인덱스로 갱신
parent = cur//2
# 요소 하향 이동 함수
def _percolate_down(self, cur):
# 최소힙이므로 루트 값을 smallest 변수에 저장
# cur 값은 extract 함수에 의해 가장 끝 인덱스 값이 들어온 상태
smallest = cur
# left와 right는 이진트리이므로 2*cur, 2*cur+1로 확인 가능
left = 2 * cur
right = 2 * cur + 1
# 자식 인덱스가 저장 배열 안의 값을 가리키고, 현재 값보다 자식 값이 작으면
# 현재 인덱스와 자식 인덱스를 교환
if left <= len(self) and self.items[left] < self.items[smallest]:
smallest = left
if right <= len(self) and self.items[right] < self.items[smallest]:
smallest = right
# 현재 인덱스가 바뀌었다면 == 현재 가리키는 값이 최소가 아니었다면
# 자식 인덱스와 현재 인덱스의 값을 교환
if smallest != cur:
self.items[cur], self.items[smallest] = self.items[smallest], self.items[cur]
# 하향 이동 함수 재귀호출
self._percolate_down(smallest)
# 삽입 함수 선언
def insert(self, k):
# 배열 맨 뒤에 값을 추가
self.items.append(k)
# 요소 상향 이동 함수 호출
self._percolate_up()
# 추출 함수 선언
def extract(self):
if len(self) < 1:
return None
# 현재 배열의 1번 인덱스 값을 루트로 저장
root = self.items[1]
# 배열의 1번 인덱스의 값과 마지막 값을 교환
self.items[1] = self.items[-1]
# 마지막 값을 추출
self.items.pop()
# 마지막 값이었던 값을 가리키는 1번 인덱스를 인자로 하향이동 함수호출
self._percolate_down(1)
# 꺼낸 기존 루트 반환
return root해당 구현 코드는 최소 힙 클래스에 대한 구현코드이다. 배열의 인덱스 값으로 부모, 자식을 구분하여 처리하며, 클래스로 선언된 리스트의 첫 번째 인덱스는 항상 최소 값을 나타낸다.
# 힙 정렬 함수 선언
def sorted_by_heal(lst):
# minheap을 최소 힙 클래스로 선언
minheap = BinaryMinHeap()
# 인자로 받은 배열을 전부 순회하여, minheap에 삽입
# 삽입 시 상향이동 함수가 호출되며, 정렬됨
for elem in lst :
minheap.insert(elem)
# minheap의 추출함수를 활용하여, 반환할 배열에 minheap의 모든 값을 순회하며 반환
sorted_lst = [minheap.extract() for _ in range(len(lst))]
# 정렬된 배열 반환
return list(sorted_lst)해당 힙정렬은 최소 힙을 활용한 오름차순 정렬이다. 최소힙을 선언하여 모든 요소를 최소힙을 거치게 하고, 차례로 배열에 입력해주는 단순한 형태이다.
힙 정렬의 시간복잡도
힙 정령의 시간 복잡도는 lst를 순회하면서 minheap에 넣는 경우와 minheap에서 꺼내 sorted_lst에 반환하는 두 가지 경우가 있다. 각각 꺼내는 함수와 넣는 함수를 요소의 수 n만큼 반복하는 연산이다. heap의 삽입, 추출함수는 높이인 log n만큼의 시간복잡도를 가지므로 두 경우는 각각 O(n log n)의 복잡도를 가진다. O(n log n) + O(n log n) = O(2n log n)이므로 시간복잡도는 상수를 무시하면 O(n log n)이다.
마무리
컴퓨터 정렬사 종강
