1. 튜닝 프로세스
Hyperparameters
- 학습률 α
가장 중요한 하이퍼파라미터 - 모멘텀 β
주로 튜닝 기본값 0.9 - Adam 최적화 알고리즘의 하이퍼파라미터 β1, β2, ε
β1=0.9, β2=0.999, ε=10^-8을 항상 사용 - 층의 수
- 층에서 은닉 유닛의 숫자
자주 튜닝 - 학습률 α + 학습률 감쇠
- 미니배치의 크기
최적화 알고리즘을 효율적으로
- 빨강>주황>보라
Try random values: Don't use a grid
-
격자점을 탐색하는 것이 일반적
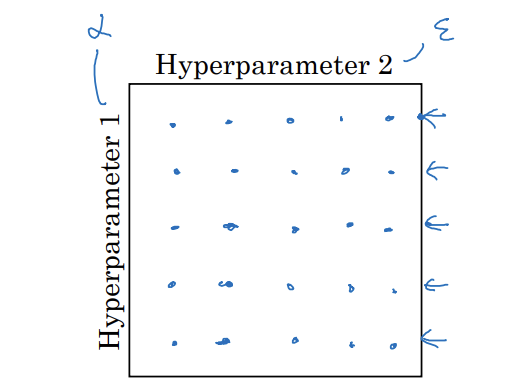
-
딥러닝에서는 무작위로 점들을 선택
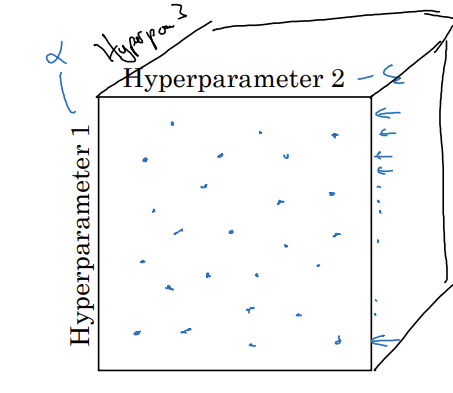
- 이유:
- 어떤 하이퍼파라미터가 문제 해결에 더 중요한지 미리 알 수 없기 때문
- 가장 중요한 하이퍼파라미터의 다양한 값을 탐색 가능
- 이유:
-
하이퍼파라미터 3개를 탐색하면 정육면체 사용
-
실제로는 3개보다 더 많은 하이퍼파라미터르 탐색하곤 함
-
다른 일반적 방법: 정밀화 접근
Coarse to fine
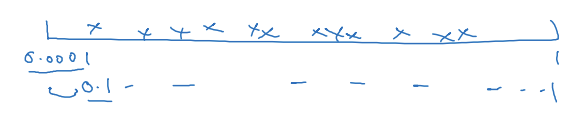
- 정밀화 접근: 더 작은 영역으로 확대해서 더 조밀하게 점들을 선택
- 파란색 사각형 안에 초점을 두고 탐색
2. 적절한 척도 선택하기
Picking hyperparameters at random
- 무작위하게 뽑는 것이 합리적인 경우
- n^[l]=50,...,100 중 무작위 선택
- layer의 수 2-4
- 그러나, 모든 하이퍼파라미터가 이렇지는 않음
Appropriate scale for hyperparameters
α=0.0001,...,1
- 90%의 샘플은 0.1과 1 사이를 탐색하고 단 10%만을 0.0001과 0.1 사이를 탐색하는데 사용
-> 합리적이지 x

- 선형 척도 대신 로그 척도에서 하이퍼파라미터를 찾는 것이 더 합리적
-> 0.0001과 0.001 사이, 0.001과 0.01 사이를 탐색할 때 더 많은 자원 사용 가능
파이썬 구현

r=-4*np.random.rand()
-> r은 -4와 0 사이의 무작위 값
α=10^r
-> 10^-4,...,10^0
10^a,...,10^b
r은 a와 b 사이에서 균일하게 무작위로 뽑힘
-> α=10^r
- 낮은 값에서 log를 취해서 a를 찾고 10^a에서 10^b까지를 로그 척도로 탐색
- r을 a와 b 사이에서 균일하게 무작위로 뽑기
Hyperparameters for exponentially weighted averages
-
지수가중평균을 계산할 때 사용되는 하이퍼파라미터 β=0.9,...,0.999
-
0.9와 0.999 사이를 균일하게 무작위 탐색하는 것은 합리적이지 않음
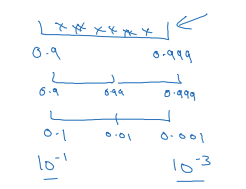
-> 1-β에 대해서 값을 탐색
1-β=0.1,...,0.001
10^-1 10^-3
1-β=10^r
β=1-10^r -
-3과 -1 사이에서 균일하게 무작위로 값을 뽑기
-
적절한 척도 위에서 무작위로 하이퍼파라미터 샘플을 추출
-> 0.9~0.99, 0.99~0.999 탐색할 때 동일한 양의 자원을 사용 가능
수학적 증명
- β가 1에 가까우면 β가 아주 조금만 바뀌어도 결과가 아주 많이 바뀜
- β=0.9 -> 0.9005: 결과에 거의 영향 x -> 대략 10개의 값을 평균
- β=0.999->0.9995: 알고리즘의 결과에 큰 영향 -> 대략 2000개의 값을 평균
- 1/(1-β) 식이 β가 1에 가까워질수록 작은 변화에도 민감하게 반응
3. 하이퍼파라미터 튜닝 실전
Re-test hyperparameters occsionally
- 한 어플리케이션에서 얻은 하이퍼파라미터에 대한 직관이 다른 영역에서 쓰일 수도, 아닐 수도 있음
- 딥러닝 분야의 사람들이 다른 영역에서 영감을 얻기 위해 그 분야의 논문을 점점 많이 찾아 읽고 있음
- 하지만, 하이퍼파라미터를 얻는 과정은 그렇지 못하다는 직관을 얻음
- 2가지 방법 사용
1) Babysitting one model
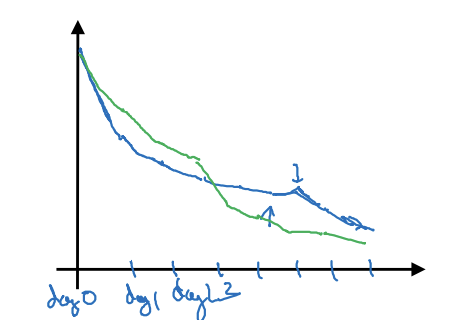
- 모델 돌보기: 성능을 잘 지켜보다가 학습 속도를 조금씩 바꾸는 방식
- 데이터는 방대하지만 CPU, GPU 등 컴퓨터 자원이 많이 필요하지 않아서 적은 숫자의 모델을 한번에 학습시킬 수 있을 때 사용
- 판다 접근
2) Training many models in parallel
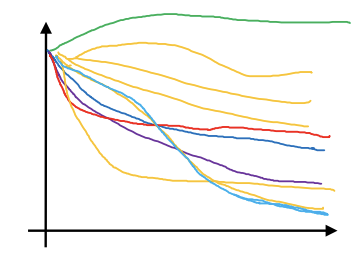
- 여러 모델을 한번에 학습
- 동시에 다른 모델의 다른 하이퍼파라미터 설정을 다루기 시작
- 마지막에는 최고 성능을 보이는 것을 고름
- 캐비어 접근
- 두 접근 중 뭘 선택할지는 컴퓨터 자원의 양과 함수 관계에 있음
- 여러 모델을 동시에 학습시키기에 충분한 컴퓨터 -> 캐비어 접근
- 학습시키고자 하는 모델이 너무 큼 -> 판다 접근
해당글은 부스트코스의 [딥러닝 2단계] 5. 하이퍼파라미터 튜닝 강의를 듣고 작성한 글입니다.