[딥러닝 2단계] 6. 배치 정규화

1. 배치 정규화

배치 정규화: 하이퍼파라미터 탐색을 쉽게 만들어줄 뿐만 아니라 신경망과 하이퍼파라미터의 상관관계를 줄여줌
-> 더 많은 하이퍼파라미터가 잘 작동

Normalizing inputs to speed up learning

로지스틱 회귀

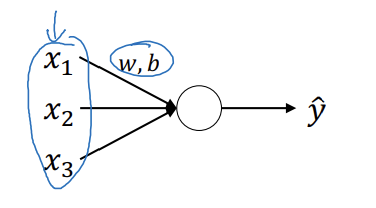
• 입력 변수 정규화 -> 학습 빨라짐
  

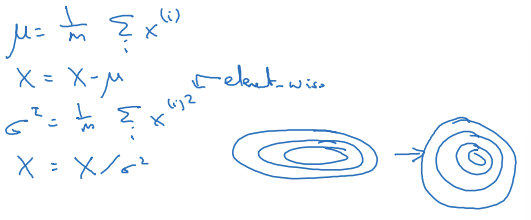
심층 신경망

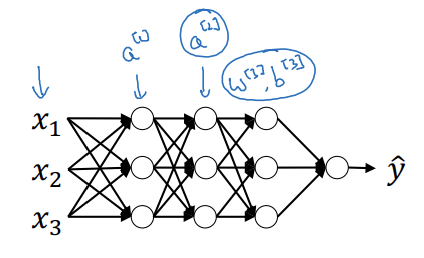
• w^[3]이나 b^[3]을 빠르게 학습시킬 수 있도록 a^[2]같은 값을 정규화할 수 있는가?
  = z^[2]를 정규화
• 활성함수 이전 값이 z^[2]를 정규화하는 것이 더 자주 쓰임

Implementing Batch Norm

• 신경망에서 사잇값들이 주어졌다고 할 때 은닉유닛의 값 z^(1)부터 z^(m) ($z^{[l](i)}$)까지 있다고 하자
  
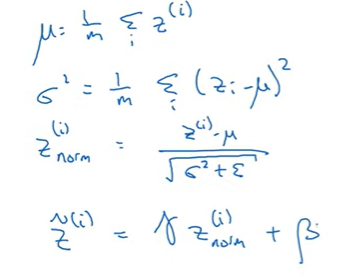
• γ와 β는 모델에서 학습시킬 수 있는 변수
• γ와 β를 이용해 z~의 평균을 원하는 대로 설정 가능
  • 
  • 정규화 과정은 항등함수를 만드는 것과 똑같은 효과를 낸 것
  • 다른 γ와 β 값을 정한다면 은닉 유닛의 값들이 서로 다른 평균이나 분산 값을 만들게 할 수 있음
• 배치 정규화는 입력층에만 정규화를 하는 것이 아니라 신경망 안 깊이 있는 은닉층의 값들까지도 정규화하는 것
  • 은닉 유닛 z의 평균과 분산을 정규화
• 입력층, 은닉 유닛 학습시킬 때 차이점: 은닉 유닛 값의 평균/분산이 0,1로 고정되기를 원치 않음
  • ex) 시그모이드 활성 함수

은닉유닛은 표준화된 평균과 분산을 갖되 평균과 분산은 학습 알고리즘에서 설정할 수 있는 두 변수 γ와 β에 의해 조절

2.배치 정규화 적용시키기

Adding Batch Norm to a network

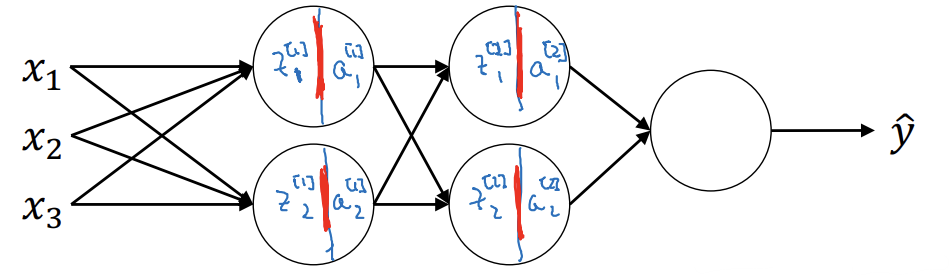
첫번째 층

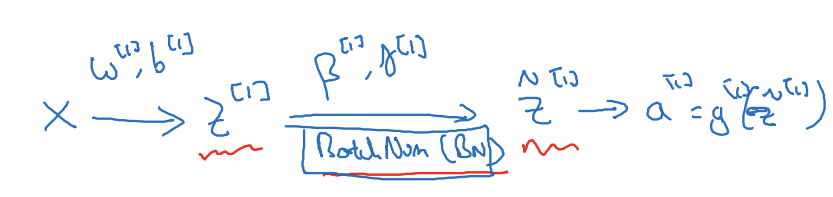
• 배치 정규화를 사용하지 않는다면 w^[1], b^[1]에 따라 우선 z^[1]을 계산
• 배치정규화에서는 z^[1]을 받아 γ^[1], β^[1]의 영향을 받아 정규화된 $\tilde{z}^{[1]}$값 얻음
  • $a^{[1]}=g^{[1]}( \tilde z^{[1]})$
• 배치 정규화는 z,a를 계산하는 사이에 이루어짐

두번째 층

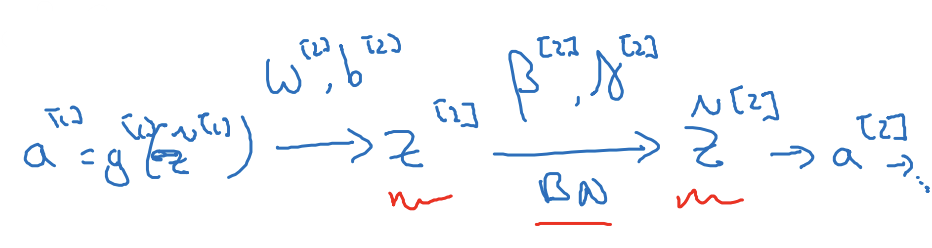
파라미터

• 배치 정규화에서 사용되는 β^[1],β^[2]는 모멘텀이나 단일, RMSprop 알고리즘에 쓰이는 하이퍼파라미터 β와 다름
• 딥러닝 프레임워크 코드: tf.nn.batch-normalization 이용

Working with mini-batches

• 배치 정규화가 훈련 집합의 각 미니 배치에 적용

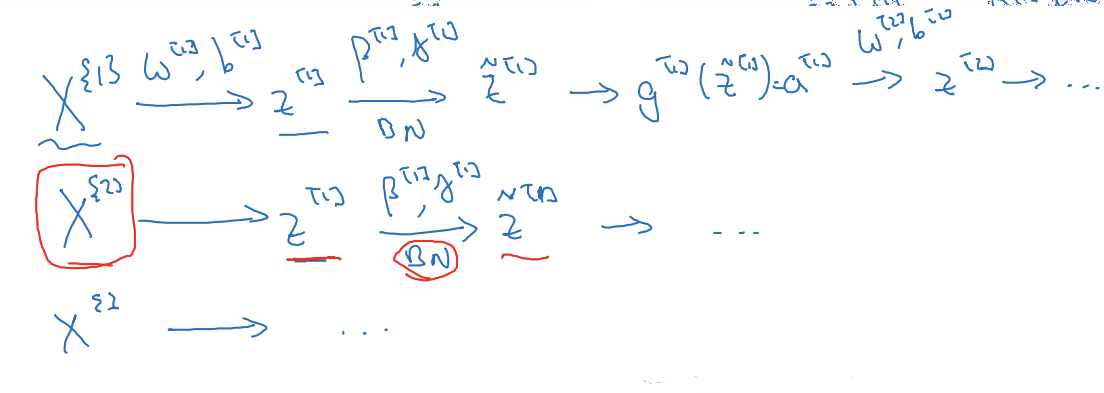
• 배치 정규화: 미니 배치를 보고 z^[l]이 평균 0, 분산 1을 갖도록 정규화한 뒤 γ와 β를 이용하여 값을 조정

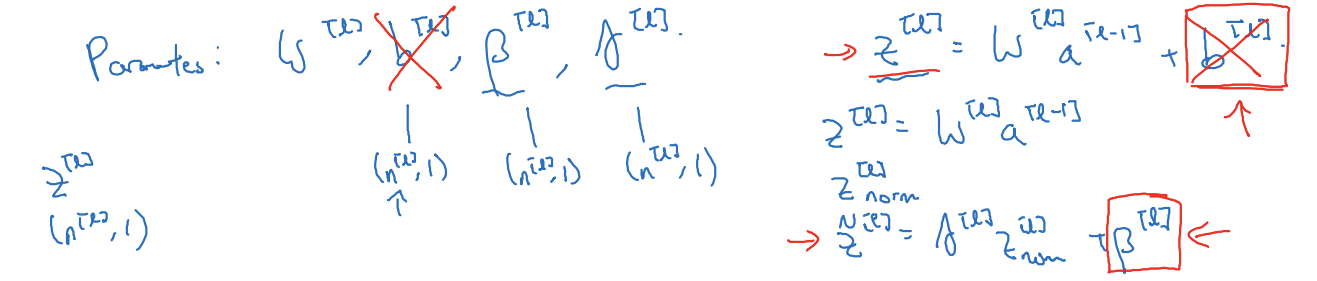
• b^[l]은 값이 무엇이든 없어짐
  • 배치 정규화의 정규화 과정에서 z의 평균을 계산한 뒤에 빼주기 때문
  • 즉, 배치 정규화를 쓴다면 b^[l]을 없앨 수 있음

• 배치 정규화가 z^[l]의 평균을 0으로 만들기 때문에 b^[l]이라는 변수가 필요 없음
• β^[l]이 그 역할을 차지

• β^[l], γ^[l]: b^[l]과 동일하게 (n^[l],1)

Implementing gradient descent

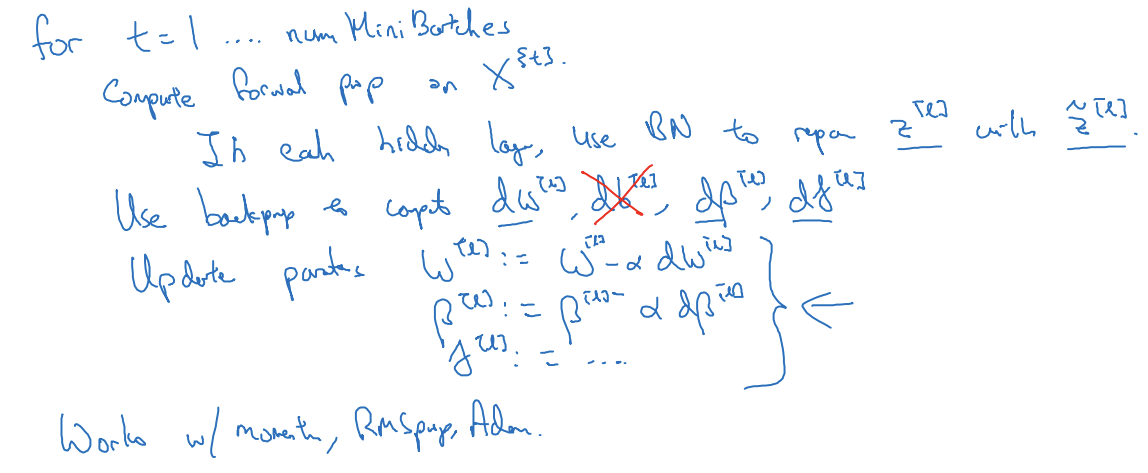
• 순방향 전파: 미니배치의 평균과 표준편차를 이용해서 z^[l] -> z~^[l]
• 역방향 전파: dw,db,dβ,dγ 계산
  • b는 제거했으니 생각 x
• 각 변수 업데이트

3. 배치 정규화가 잘 작동하는 이유는 무엇일까요?

1. 입력 특성 X를 평균 0, 분산 1로 정규화하는 것이 학습 속도를 올림
   -> 배치 정규화가 작동하는 이유가 은닉층과 입력층에서 비슷한 일을 하기 때문이라는 직관

Learning on shifting input distribution

2. 신경망에서 깊은 층의 가중치가 앞쪽 층의 가중치의 변화에 영향을 덜 받음
   ex) 고양이 분류
   

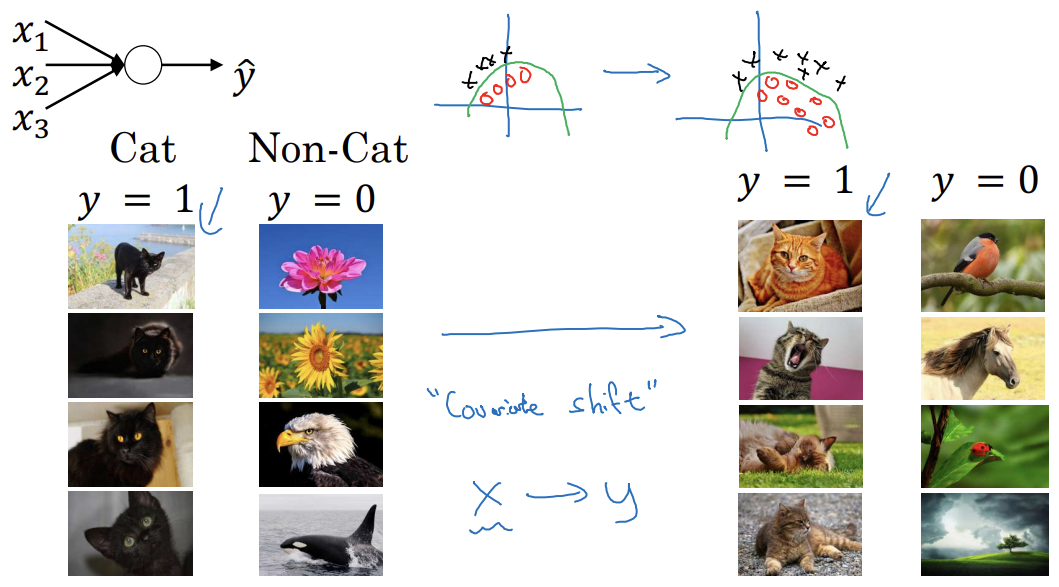
   • 검정 고양이의 이미지만 써서 학습한 후 다양한 색의 고양이에게 적용 신경망이 좋은 성능을 내지 못함
     • 함수는 동일하지만 학습할 때의 데이터 분포가 다르기 때문
   • 데이터 분포가 변화하는 것: 공변량 변화

공변량 변화: X,Y간의 대응을 학습시킬 때 X의 분포가 바뀐다면 학습 알고리즘을 다시 학습해야함

Why this is a problem with neural networks?

세번째 은닉층의 관점

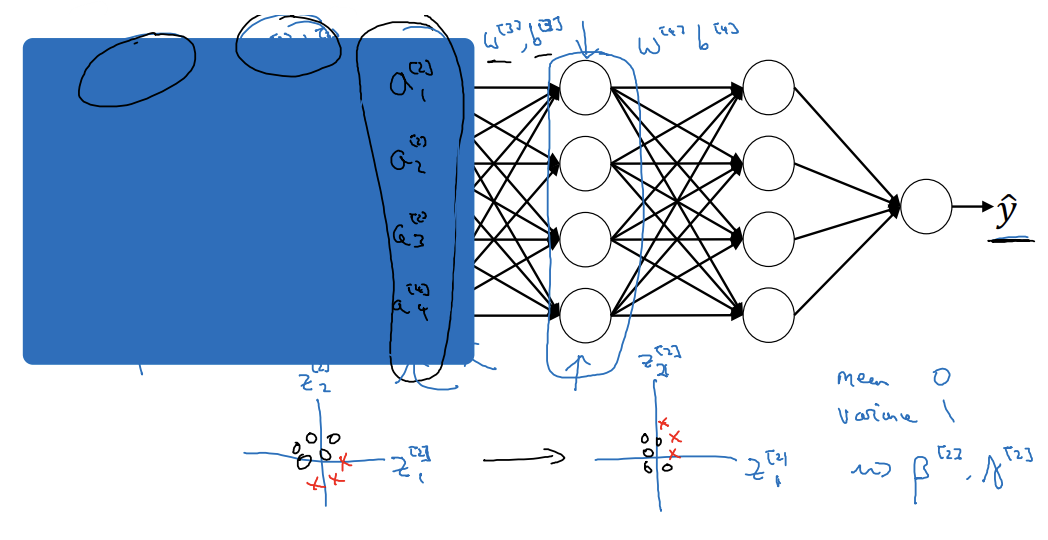
• 매개변수의 값이 변화하면 a^[2]의 값들도 바뀜
  • 두번째 은닉층의 값들이 계속 바뀌고 있음
    -> 공변량 변화
• 배치 정규화: 은닉층 값들의 분포가 변화하는 양을 줄여줌
• z^[2]_1과 z^[2]_2의 값이 바뀌더라도 평균과 분산은 0,1처럼 유지
  • β^[2], γ^[2]와 같은 값도 가능

배치 정규화: 앞선 층에서의 매개변수가 바뀌었을 때 세번째 층의 값이 받아들여서 학습하게 될 값의 분포를 제한
-> 입력값이 바뀌어서 발생하는 문제를 안정화

• 앞쪽 층의 매개변수와 뒤쪽 층의 매개변수 간의 관계를 약화

Batch Norm as regularization

규제 효과

• 각각의 미니 배치 X^t가 가진 z^[l]에 대해서 그 미니 배치의 평균과 분산에 따라 값을 조정
  • 미니배치로 계산한 평균과 분산은 전체 데이터의 일부로 추정한 것이므로 잡음을 갖고 있음
• z^[l]에서 z~^[l]로 조정하는 과정 역시 잡음이 있음
  • 잡음이 끼어 있는 평균과 분산으로 계산하기 때문
  • 드롭아웃처럼 은닉층의 활성 함수에 잡음이 끼어 있음
    • 드롭아웃: 은닉층에 확률에 따라 0,1을 곱해 곱셈 잡음을 갖고 있음
  • 배치 정규화: 표준편차로 나누니 곱셈 잡음, 평균을 빼니 덧셈 잡음 -> 약간의 일반화 효과
• 큰 미니배치를 사용하면 잡음이 줄어들고 일반화 효과도 줄어들 것
  • 그러므로, 배치 정규화를 일반화 목적으로 사용하지는 않음
  • 학습 속도를 올리는 용도로 사용

4. 테스트시의 배치 정규화

• 배치 정규화는 한 번에 하나의 미니배치 데이터를 처리
• 하지만, 테스트에서는 한 번에 샘플 1개씩을 처리해야함

Batch Norm at test time

학습 중 배치 정규화를 위해 사용했던 식

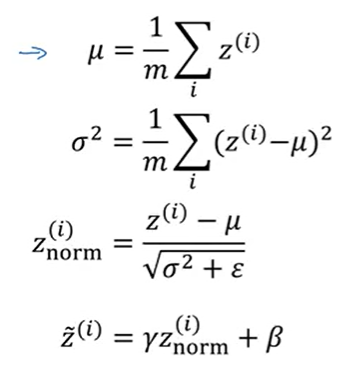
• m: 미니 배치 안의 샘플 수

• z~는 z_norm을 γ와 β을 써서 조정한 것

• µ, σ^2은 미니 배치 안에서 계산되지만 테스트 과정에서는 64,128,256개 등의 샘플을 포함하는미니배치가 없으므로 동시에 처리 불가
  -> 처리할 다른 방법 필요

• µ, σ^2: 여러 미니 배치에 걸쳐서 구한 지수가중평균을 추정치로 사용

• 미니 배치 X^{1}, X^{2}등과 대응하는 값 Y 존재

1. L층에 대해서 X^{k}를 학습시켜 µ^{k}[l] 값을 얻음
2. 지수가중평균을 이용해서 θ1,θ2,θ3,..의 평균을 계산
   -> 지수 가중평균=그 은닉층의 z값 평균의 추정치
   => µ, σ^2의 이동 평균 추정
3. test 과정에서 z, µ/σ^2의 지수가중평균을 이용해 z_norm 계산
4. z_norm, 신경망 학습 과정에서 학습시킨 γ,β 매개변수를 이용해 z~ 계산

• 학습과정 중 µ, σ^2는 미니 배치로 계산, 테스트할 때는 한 번에 샘플 하나를 처리

---

해당글은 부스트코스의 [딥러닝 2단계] 6. 배치 정규화 강의를 듣고 작성한 글입니다.