[딥러닝 4단계] 2. 케이스 스터디

1. 왜 케이스 스터디를 하나요?

• 합성곱 신경망을 구축하기 위해서는 효과적인 신경망 구조를 살펴봐야 함
• 하나의 컴퓨터 비전 작업에서 잘 작동하는 신경망의 구조는 다른 작업에서도 잘 작동하는 경우가 많음

Outline

• LeNet-5
• AlexNet
• VGG
• ResNet: 152개의 층을 훈련시키고 흥미로운 개념을 가지고 있음
• Inception

2. 고전적인 네트워크들

• LeNet-5, AlexNet, VGG

LeNet-5

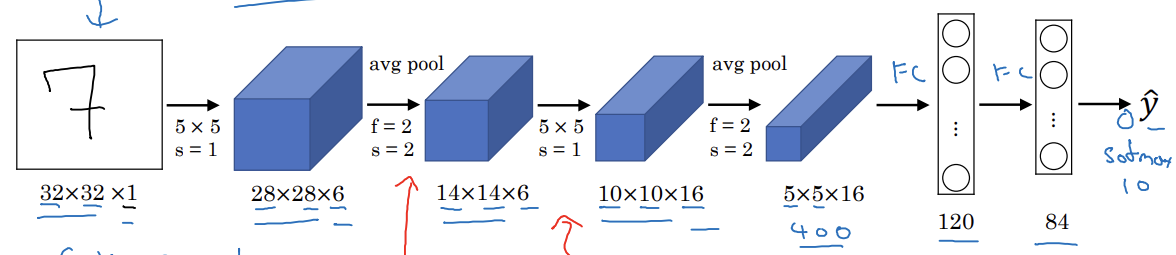
• 32x32x1의 흑백 이미지의 손글씨 숫자 인식하기

1. 6개의 5x5 필터와 1의 스트라이드 사용
2. f=2, s=2 평균 풀링
3. 16개의 5x5 필터 사용
   • 1998년에는 패딩을 사용하지 않거나 유효 합성곱을 사용했음
     -> 합성곱 층 적용할 때마다 높이, 너비 감소
4. 풀링층
5. 완전 연결층
   • 400개의 노드를 120개의 뉴런에 각각 연결
6. 완전 연결층
7. 최종 출력
   • 지금은 softmax층을 사용하지만 LeNet-5는 요즘은 잘 사용하지 않는 분류기 사용

• 요즘 기준으로 적은 60000개의 변수를 가짐
• 깊이가 깊어질수록 높이와 너비가 감소
• 채널 수는 증가
• 층의 배치가 요즘도 사용됨
  • 몇 개의 합성곱 층 뒤에 풀링 층이 따라오고 다시 합성곱 층, 풀링 층, 완전 연결 층이 오는 구조

논문

• 당시 사람들은 sigmoid, tanh 비선형성 사용, ReLU 사용 x
• 초기의 LeNet-5는 각각의 필터가 서로 다른 채널에 적용
• 비선형성이 풀링층 뒤에 있음

AlexNet

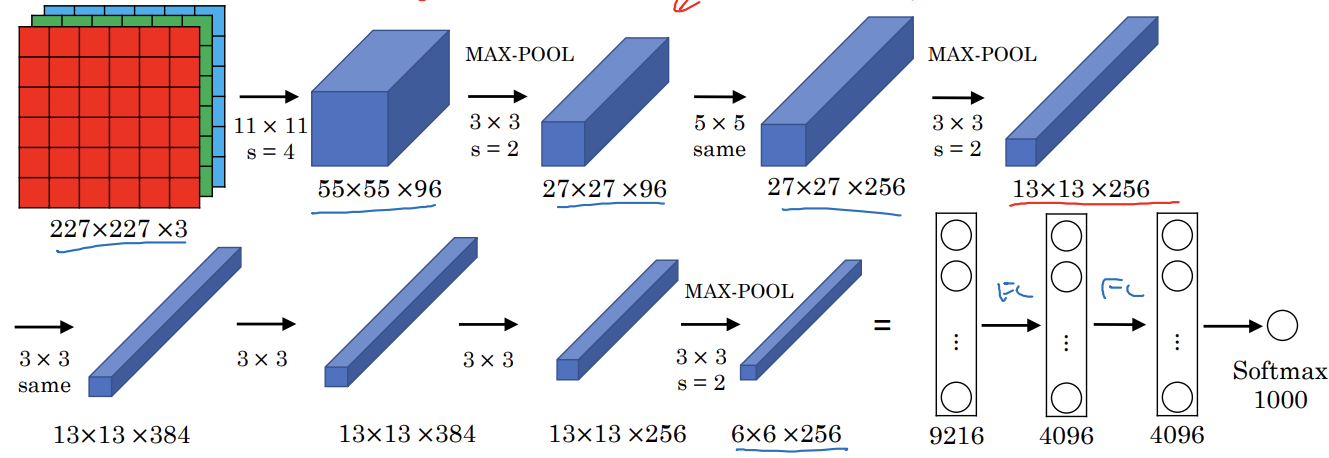
• 227x227x3의 이미지로 시작

1. 96개의 11x11 필터 사용, 4의 스트라이드
   • 크기가 1/4로 줄어듬
2. 3x3 크기와 2의 스트라이드인 최대 풀링
3. 5x5 동일 합성곱 연산
4. 최대 풀링
5. 3x3 동일 합성곱
6. 3x3 동일 합성곱
7. 3x3 동일 합성곱
8. 최대 풀링
9. 9216개의 노드로 완전 연결층
10. 완전 연결층
11. softmax로 1000개의 출력

• LeNet과 유사하지만 훨씬 크기가 큼
  • 6만개 -> 6천만 개 정도의 매개변수
• ReLU 활성화 함수 사용
• 지역 응답 정규화(LRN)

VGG-16

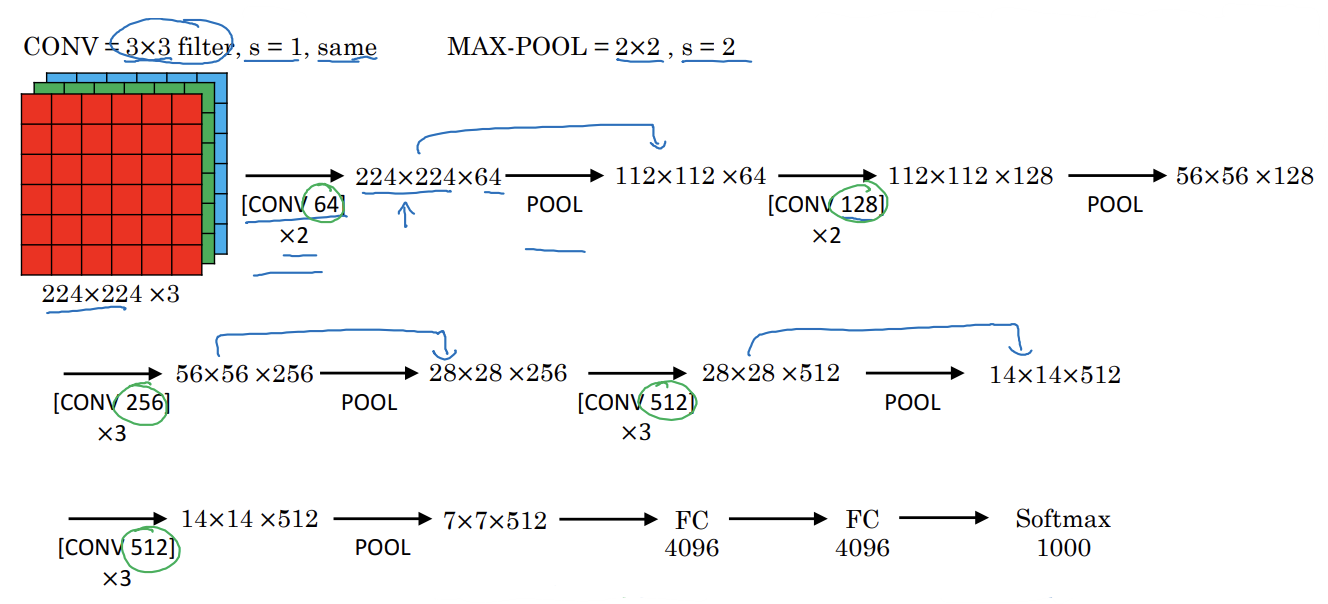
• 많은 하이퍼 파라미터를 가지는 대신 합성곱에서 스트라이드가 1인 3X3 필터만을 사요해 동일합성곱을 하고 최대 풀링층에서는 2의 스트라이드의 2x2를 사용

1. 첫 두 층 64개의 필터로 합성곱
2. 풀링층
3. 128개의 필터를 가진 동일 합성곱층
4. 풀링층
5. 256개의 필터를 가진 3개 합성곱층
6. 풀링층
   ...
   완전연결층

• 16개의 가중치를 가진 층이 존재
• 1억 3천 8백만 개 정도의 변수를 가진 상당히 큰 네트워크
• 균일하게 높이와 너비를 감소
• VGG-19는 이것보다 더 큰 버전

3. Resnets

• 깊은 신경망은 경사 소실, 경사 폭발 문제 존재
  -> 스킵 연결: 한 층의 활성값을 가지고 훨씬 깊은 층에 적용하는 방식

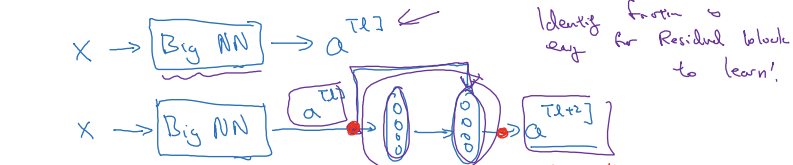
Residual block

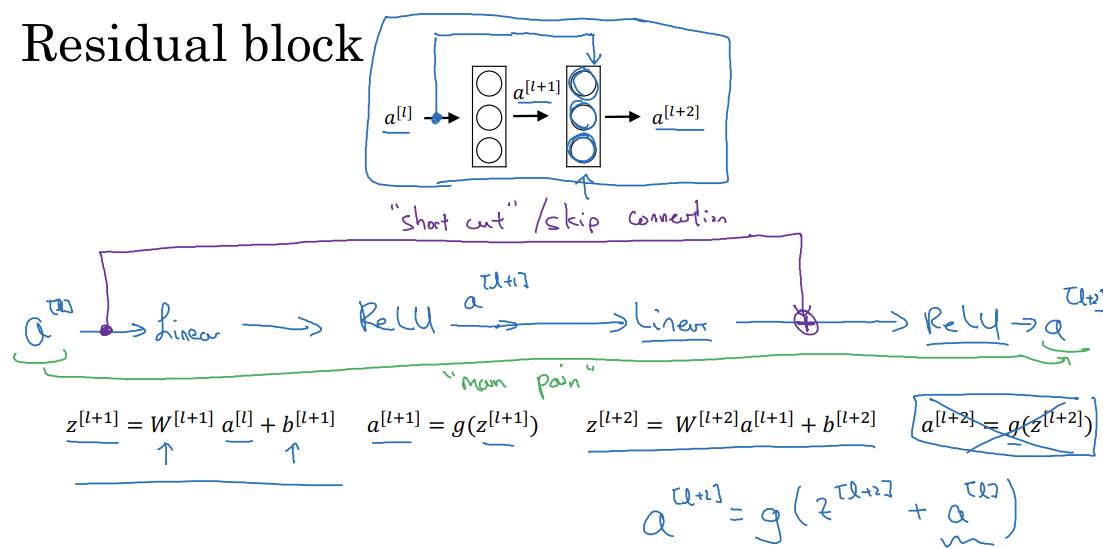
• main path: a^[l] -> 선형 연산 -> ReLU -> 선형 연산 -> ReLU -> a^[L+2]
• short cut(스킵 연결): a^[l]을 복제해서 신경망의 먼 곳까지 보낸 후 ReLU 적용 전에 더해줌
• 잔여 블록을 사용하면 훨씬 깊은 신경망을 훈련시킬 수 있음
• 잔여 블록들을 쌓아서 ResNet을 만듬

Residual Network

• Resnet을 만드려면 평형망에 스킵 연결을 더해주어야 함
• 다섯 개의 잔여블록으로 이루어진 ResNet
  

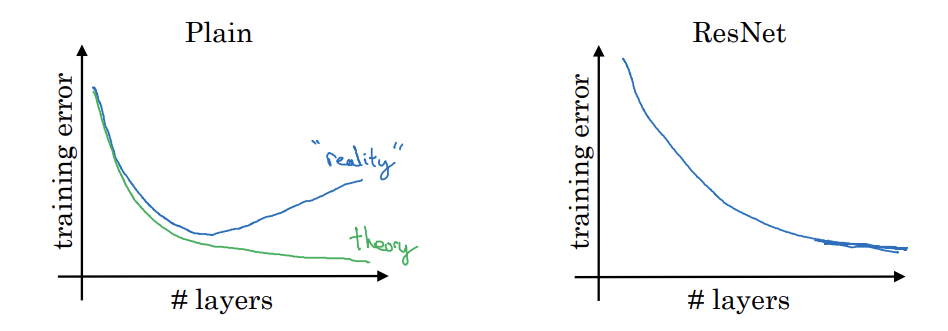
Plain

• 경험적으로 층의 개수를 늘릴 수록 훈련 오류는 감소하다가 다시 증가
• 이론 상으로는 신경망이 깊어질 수록 훈련 세트에서 오류는 계속 낮아짐

Resnet

• ResNet 에서는 훈련오류가 계속 감소하는 성능을 가질 수 있음
  -> 더 깊은 신경망 훈련에 효과적

4. 왜 ResNets 이 잘 작동할까요?

Why do residual networks work?

• ReLU 함수를 사용하므로 활성값>=0
  
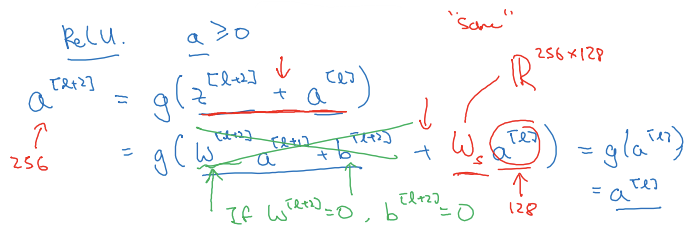
• 만약 W^[l+2], b^[l+2]=0이라면 a^[l+2]=g(a^[l])=a^[l]
• 항등함수를 학습하면 되므로 신경망에 두 층을 추가해도 두 층이 없는 더 간단한 네트워크만큼의 성능을 가짐
  -> 잔차 블록을 거대한 신경망 어딘가에 추가해도 성능에 지장이 없는 이유
• 스킵 연결 없이 네트워크를 깊게 만드려고 하면 변수 선택이 어려워짐
  -> 성능 저하
• 동일 합성곱이 차원을 유지시켜주어서 덧셈 가능

ResNet

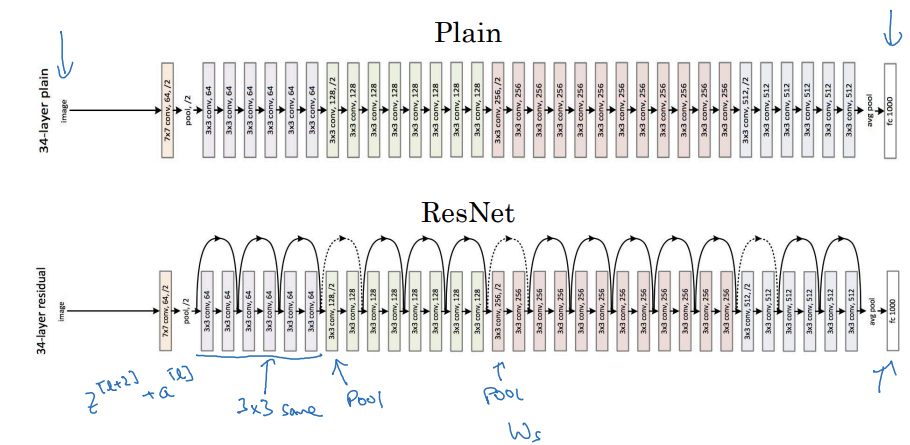
• 스킵 연결을 추가해줌
• 3x3 합성곱 중 대부분은 동일 합성곱

5. Network 속의 Network

Why does a 1x1 convolution do?

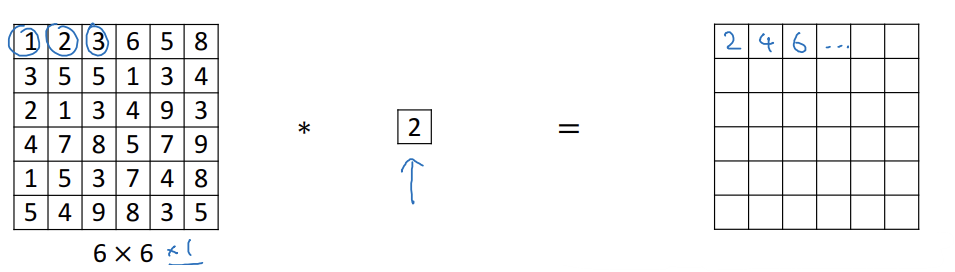
• 6x6 이미지를 1x1 필터와 합성곱 연산하면 2만큼 곱해주는 것과 동일
• 유용해보이지 않음
  
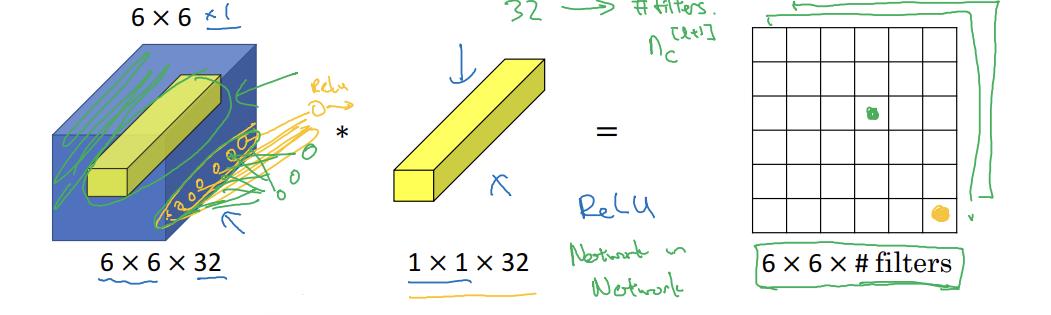
• 6x6x32라고 하면 훨씬 의미 있음
• 입력 채널의 수만큼 유닛을 입력으로 받아서, 이들을 하나로 묶는 연산과정 통해, 출력채널의 수만큼 출력을 하는 작은 신경망 네트워크로 간주
• 완전 연결 신경망을 36개의 위치에 각각 적용해서 32개의 숫자를 입력값으로 받고 필터의 수만큼 출력하는 것
  • 결과: 6x6xfilters
  • = 네트워크 안의 네트워크

Using 1x1 convolutions

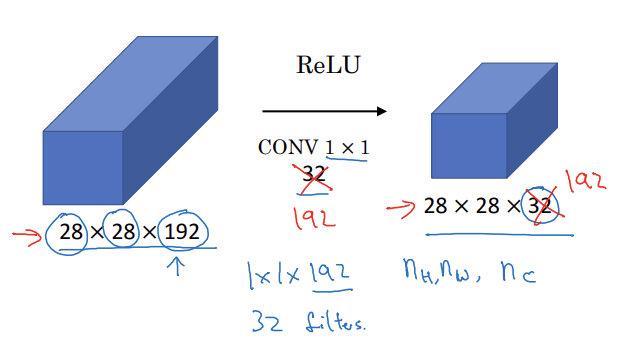
• 채널의 수가 너무 많아서 줄일 때 32개의 1x1x192 필터를 사용
  • n_c를 줄이는 방법
• 네트워크에 비선형성을 더해줌

6. Inception 네트워크의 아이디어

Motivation for inception network

• 인셉션 네트워크는 필터의 크기를 정하지 않고 합성곱 또는 풀링 층을 모두 사용하는 것
• 1x1 합성곱을 이용하면 28x28x64
• 3x3 을 이용하면 28x28x128이 되고 이 두번째 볼륨을 첫번째 볼륨 위에 쌓음
  • 동일 합성곱을 사용해서 출력이 28x28로 유지되게 함
• 5x5 필터를 이용하면 28x28x32
• 풀링 층의 출력도 이용
• 인셉션 모듈의 출력 32+32+128+64=256이므로 28x28x256

  인셉션 네트워크는 필터의 크기나 풀링을 결정하는 대신 전부다 적용해서 출력들을 합친뒤 네트워크로 하려금 스스로 변수나 필터 크기의 조합을 학습하게 만드는 것

The problem of computational cost

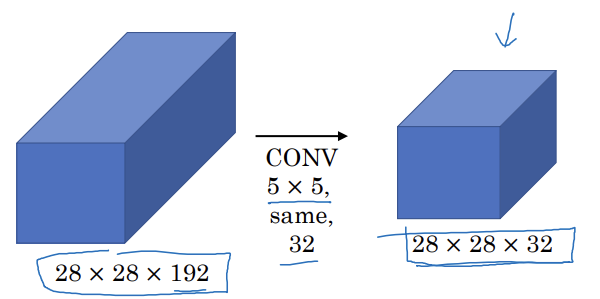
• 32개의 필터, 각 필터는 5x5x192
• 28x28x32 x 5x5x192 = 1억 2천만
  • 비용이 큰 계산
    -> 1x1 합성곱을 사용하면 계산을 1/10 정도로 줄일 수 있음

Using 1x1 convolution

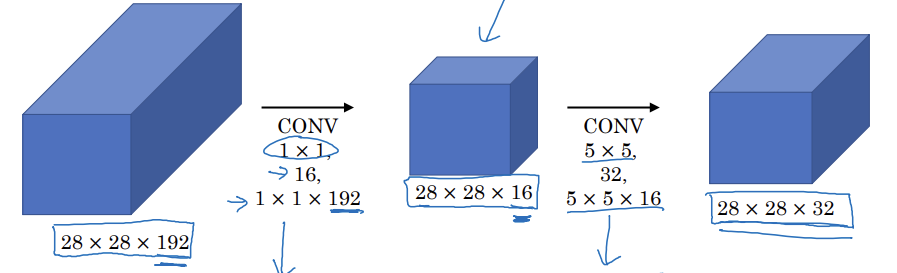
• 1x1 합성곱으로 채널을 16개로 줄이고 5x5 합성곱을 하면 입력과 출력 크기가 동일
• 병목층: 네트워크에서 가장 작은 부분
• 28x28x16 x 1x1x192 = 240만
• 28x28x32 x 5x5x16 = 1천만
• 240만+1천만 = 1천 2백만 개의 곱셈으로 줄인 셈

7. Inception 네트워크

Inception module

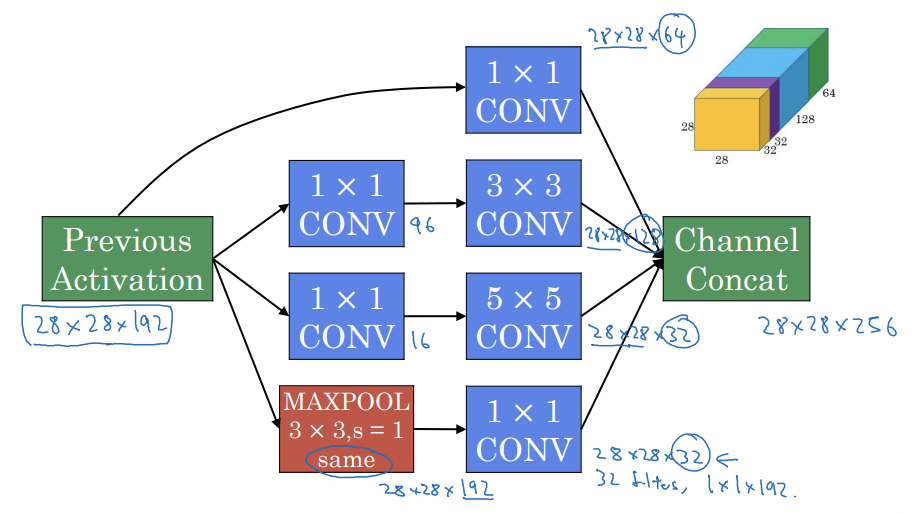
• 블록 모아서 연결하면 28x28x256 크기
• 이것이 하나의 인셉션 모듈

Inception network

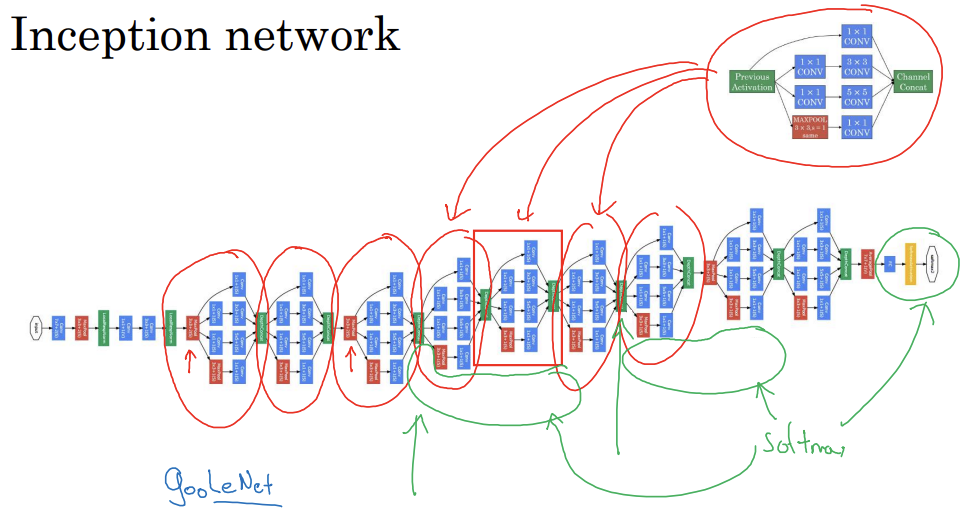
• 인셉션 네트워크는 모듈들을 하나로 모아놓은 것
• 하나의 블록이 인셉션 모듈
• 네트워크의 마지막 몇 개의 층은 완전 연결 층
• 그 뒤에는 예측을 위한 소프트맥스층이 있음
• 은닉층이나 중간 층에서 계산된 특성들도 예측 결과가 나쁘지 않음
  • 정규화 효과, 네트워크 과대적합 방지
• GoogLeNet이라고 불림

---

해당글은 부스트코스의 [딥러닝 4단계] 2. 케이스 스터디 강의를 듣고 작성한 글입니다.