1. 컴퓨터비전
컴퓨터 비전에서의 딥러닝에 관심이 가는 두가지 이유
1. 컴퓨터 비전의 빠른 발전이 많은 새로운 애플리케이션들이 만들어지게 함
2. 컴퓨터 비전을 연구하는 사회가 창의적이고 도전적이며 새로운 신경망 구조와 알고리즘이 서로 많은 영감을 주면서 서로에 영향을 끼침
Computer Vision Problems
-
이미지 분류
-
물체 감지
물체가 있는지만 보는게 아니라 물체 주변에 네모 박스를 그리거나 다른 방식으로 물체 식별

-
신경망 스타일 변형
컨텐츠 이미지를 스타일 이미지로 나오게 하는 것
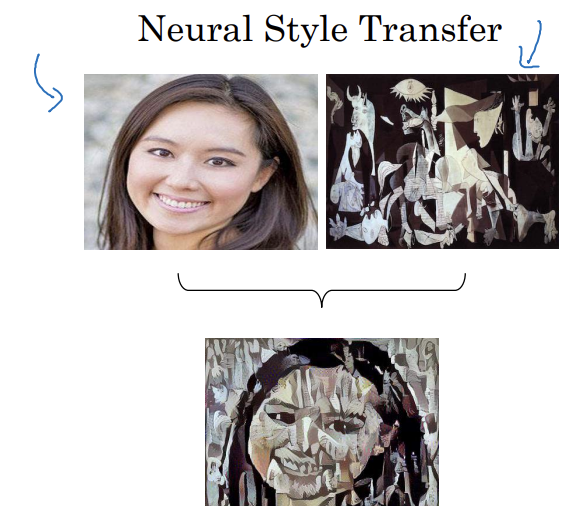
Deep Learning on large images
- 컴퓨터 비전에서 큰 장애물: 입력이 매우 클 수 있음
- 저해상도 -> 64x64x3=12288의 크기를 가지게 됨
- 고해상도 -> 1000x1000x3
- 1000x3000000의 크기를 가진
- 30억개의 매우 큰 변수를 가지게 됨
- 과적합 방지가 어려움, 계산과 메모리의 요구사항이 적합하지 않을 수 있음
- -> 합성곱 사용망에서는 이 고민을 하지 않아도 됨
2. 모서리 감지 예시
Computer Vision Problem

- 신경망의 하위 층이 모서리를 감지
- 이후의 층들이 가능성 있는 물체를 감지
- 더 이후의 층들은 온전한 물체의 부분을 살핌
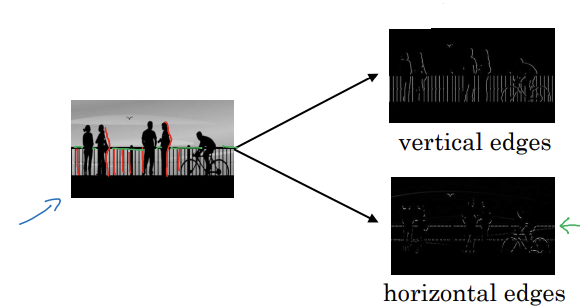
- 이미지에서 수직인 모서리 찾기
- 수평의 모서리 감지
Vertical edge detection
- 6x6x1 행렬의 그레이 스케일 이미지
- filter(필터): 수직 모서리를 알기 위해 만든 3x3 행렬
- *: 6x6 이미지를 3x3 필터로 합성곱
- 결과: 4x4 이미지
- 한 칸에 요소들의 곱셈을 더함
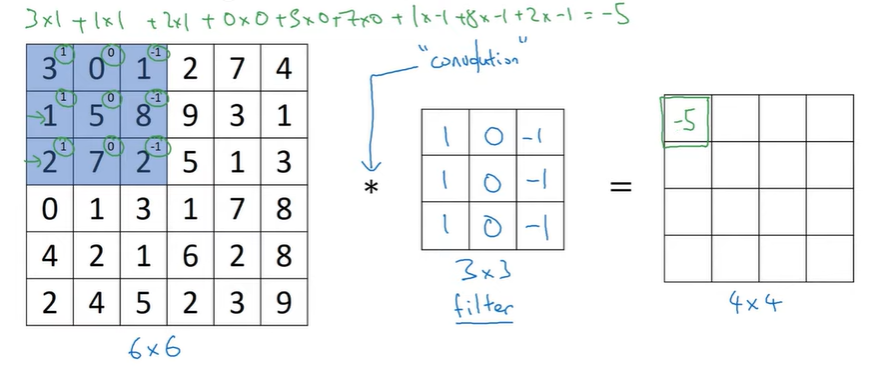
- 한 칸에 요소들의 곱셈을 더함
- 프로그래밍
- python: conv-forward
- tensorflow: tf.nn.conv2d
- keras: Conv2D
Vertical edge detection
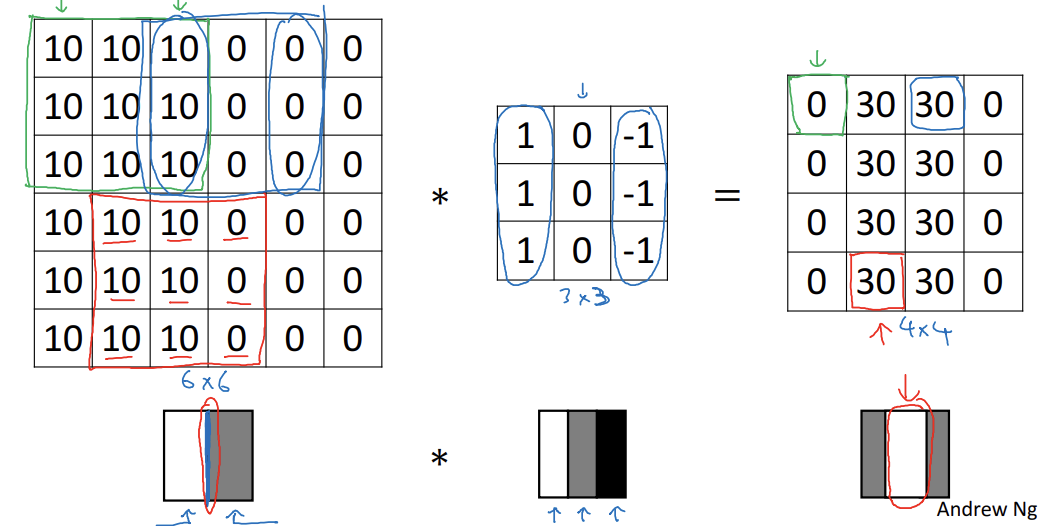
- 결과 이미지의 가운데 밝은 영역이 이미지 가운데 강한 수직 경계선이 있다는 것을 알려줌
- 3x3 필터에서 왼쪽 편에는 밝은 픽셀, 가운데는 중요하지 않고, 어둔 픽셀이 오른쪽에 있음
3. 더 많은 모서리 감지 예시
Vertical and Horizonal Edge Detection
- 가로 윤곽선 필터
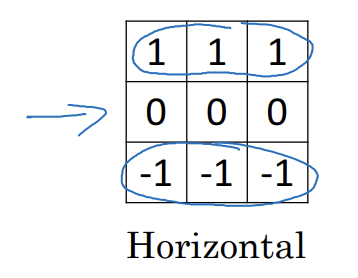
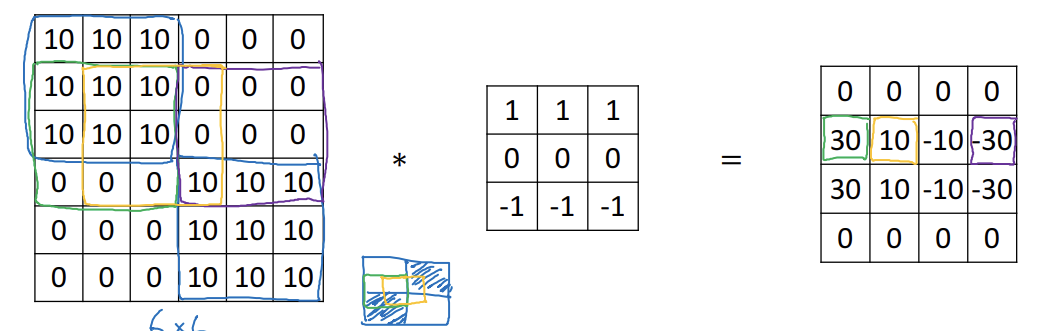
Learning to detect edges
Sobel filter
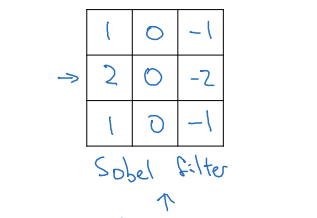
- 중간 부분의 픽셀에 더 중점을 두어 선명해 보임
Scharr filter
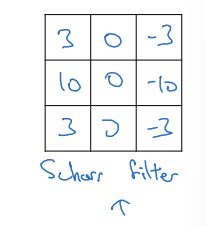
- 세로 윤곽선 검출을 위한 것이고 90도 회전하면 가로 윤곽선 검출이 됨
스스로 학습
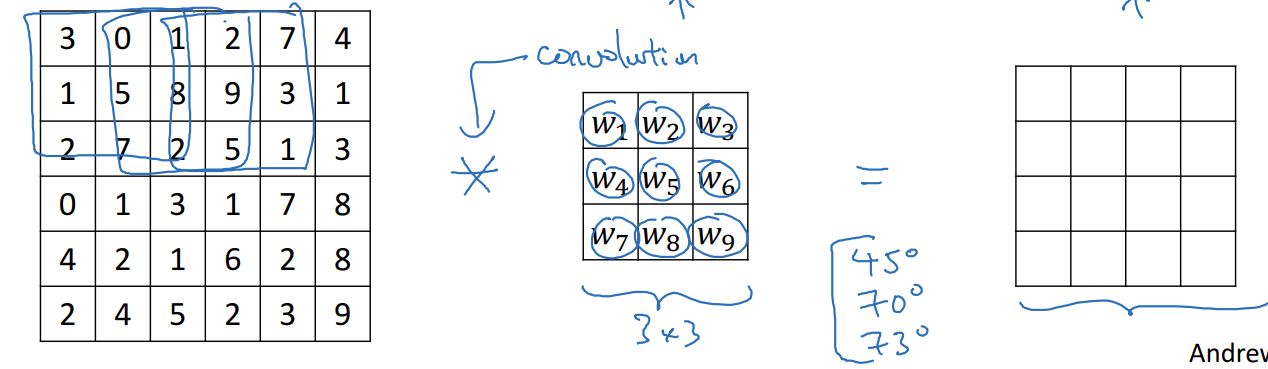
- 최근 딥러닝에서는 9개의 숫자 변수로 두고 역전파로 학습
4. 패딩 (Padding)
Padding
- nxn 이미지를 fxf 필터로 합성곱 한 결과는 (n-f+1)x(n-f+1)
두가지 단점
- 계속 합성곱 연산을 하게 되면, 이미지가 계속 축소됨
- 가장자리 픽셀은 단 한번만 사용하여 이미지 윤곽쪽의 정보를 버리게 됨
해결방안: 합성곱 연산 하기 전에 이미지를 덧대기
= 1 픽셀만큼 가장자리에 경계를 덧대기
= p=1
= (n+2p-f+1)x(n+2p-f+1)
-> 8x8 이미지
Valid and Same convolutions
유효 합성곱
- 유효 합성곱: 패딩이 없는 것
- nxn 이미지를 fxf 필터와 합성곱 해서 n-f+1xn-f+1의 결과 이미지가 나옴
동일 합성곱
- 패딩을 한 뒤 결과 이미지의 크기가 기존 이미지와 동일
- (n+2p-f+1)x(n+2p-f+1)
- n+2p-f+1=n -> p=(f-1)/2
필터의 크기 f는 홀수
1. f가 짝수라면 패딩이 비대칭이 됨
2. 중심 위치가 존재
5. 스트라이드 (Stride)
Strided convolution
- stride: 필터의 이동 횟수
- stride=2 -> 필터를 두 칸 이동
- nxn * fxf, padding=p, stride=s
- 결과의 크기: (n+2p-f)/s+1 x (n+2p-f)/s+1
- 소수점이면 내림값 사용
- ⌊z⌋=floor(z)
- 보통은 필터에 맞춰서 최대한 크기가 정수가 될수 있도록 패딩과 스트라이드 수치를 맞춤
- 소수점이면 내림값 사용
Technical note on cross-correlation vs convolution
-
일반적으로 수학에서 정의하는 합성곱은 합성곱을 하기 전에 필터를 가로축과 세로축으로 뒤집는 연산(미러링 과정)을 해줘야함

-
지금까지 배운 합성곱은 사실 교차상관 이지만 딥러닝에서는 관습적으로 합성곱이라고함
- 딥러닝에서는 뒤집는 연산을 생략함
- 뒤집는 과정은 신호처리에서는 유용하지만 심층 신경망 분야에서는 아무런 영향이 없기 때문
6. 입체형 이미지에서의 합성곱
- 3D 입체형의 합성곱
Convolutions on RGB images
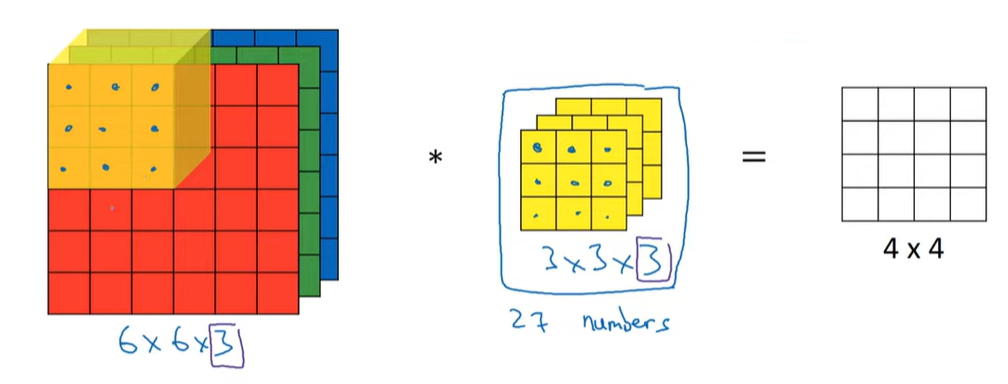
- 6x6x3 행렬
- 6: height
- 6: width
- 3: 3개의 색상 채널
- 3D 필터 사용: 3x3x3
- 이미지와 필터 크기의 마지막 숫자가 일치
Multiple filters
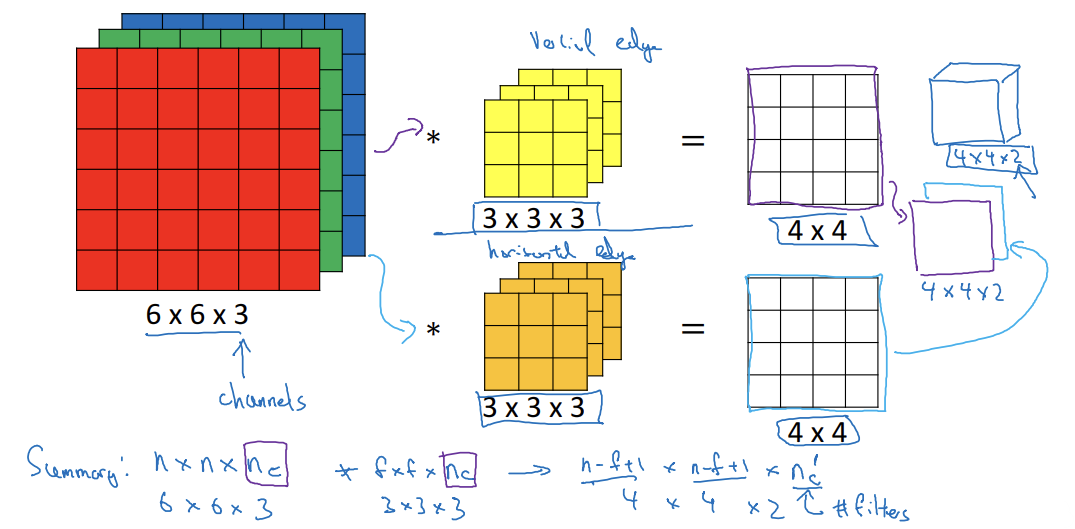
- 여러 개의 필터를 동시에 사용
- 결과: 4x4x2
- 2: 필터의 개수(n_c)
- 입력이미지: nxnxn_c * nxnxn_c
-> n-f+1 x n-f+1 x n_c' - 채널의 수=마지막 크기=3D 입체형의 깊이
7. 합성곱 네트워크의 한 계층 구성하기
합성곱 신경망의 한 계층
- 합성곱 연산 -> 편향 추가 -> 비선형성 추가(활성화 함수 ReLU)
- 6x6x3 -> 4x4x2
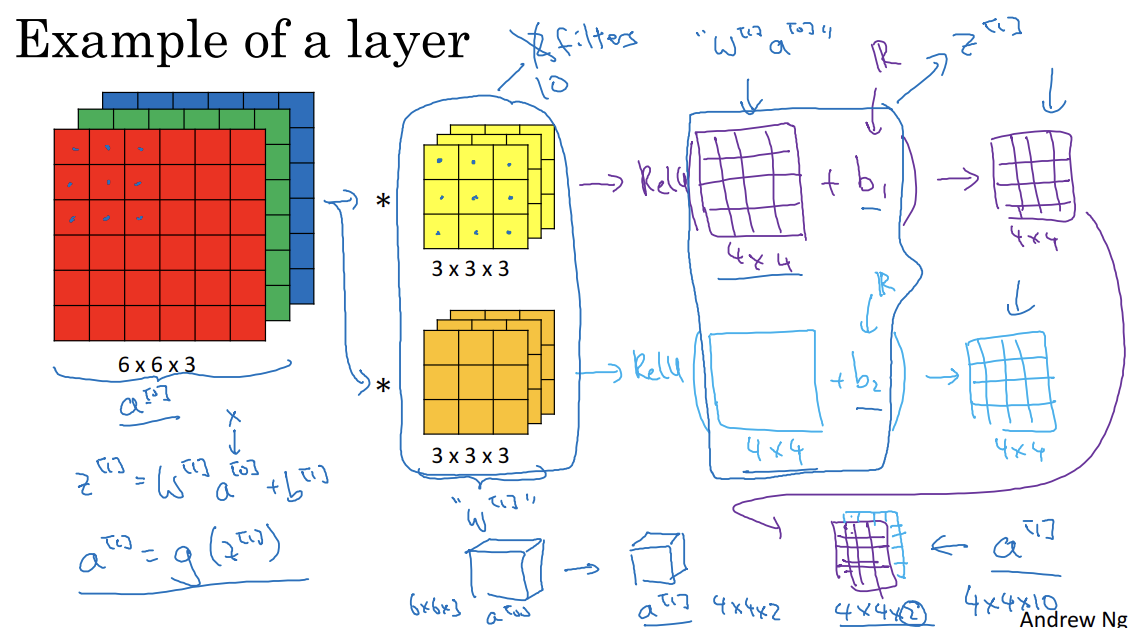
Number of parameters in one layer
- 10개의 필터, 3x3x3 크기 -> 이 층은 몇 개의 매개변수?
- 27parameters + 1 bias = 28개의 변수
- 28 x 10 = 280개의 변수
Summary of notation
- l: 합성곱 계층
- f^[l] = filter size
- p^[l] = padding
- s^[l] = stride
- Each filter is:
f^[l] x f^[l] x n_c^[l-1] - Activations:
a^[l] -> x x
A^[l] -> m x x x - Input:
x x - Output:
x x - Weights: f^[l] x f^[l] x n_c^[l-1] x n_c^[l]
- bias: n_c^[l] - (1,1,1,n_c^[l])
8. 간단한 합성곱 네트워크 예시
Example ConvNet
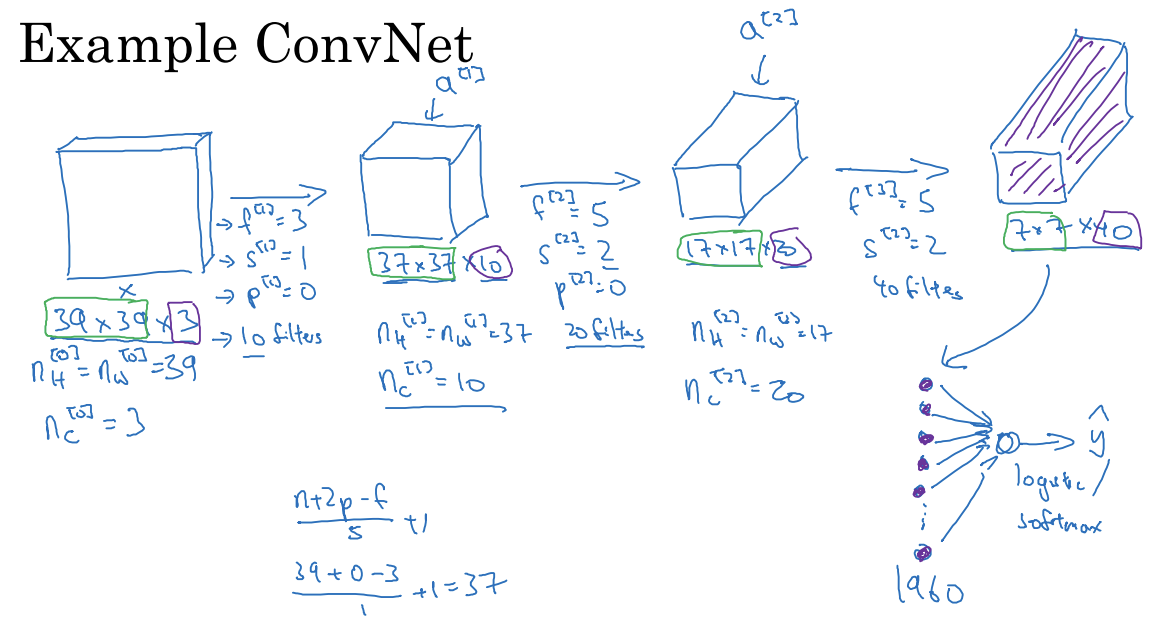
- (39+0-3)/1+1 -> 37
- 17x17x20
- 7x7x40 = 1960
- 이것을 펼쳐서 1960개의 하나의 벡터로 만든 뒤 logistic/softmax에 넣으면 최종 예측값이 됨
- 더 큰 이미지에서 시작해서 높이와 너비가 비슷하게 유지되다가 신경망이 깊어질수록 줄어듬
- 39 -> 37 -> 17 -> 7
- 채널의 수: 3 -> 10 -> 20 -> 40
Types of layer in a convolutional network
- Convolution (CONV): 합성곱층
- Pooling (POOL): 풀링층
- Fully connected (FC): 완전 연결층
9. 풀링(Pooling)층
- 풀링 층을 사용하면 표현의 크기를 줄임으로써 계산속도를 줄이고 특징을 더 잘 검출할 수 있음
Pooling layer: Max pooling
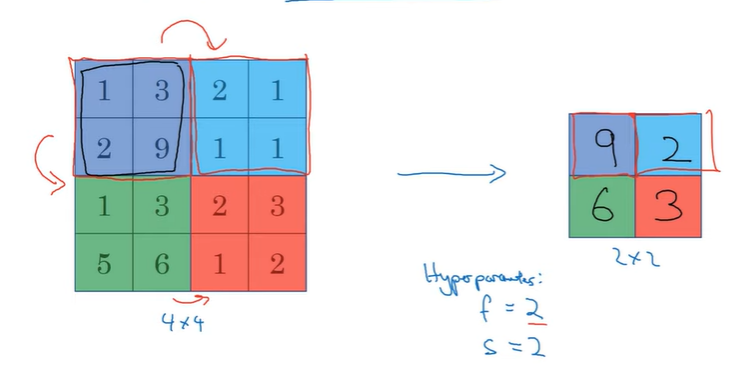
- 입력을 여러 구간으로 나눔
- 2x2 영역의 최대값을 취함
- f=2짜리 필터를 적용하는 것과 동일
- 2x2 영역과 2만큼의 스트라이드
- Hyperparameters: f=2, s=2
- 최대 연산의 역할: 이미지의 특징이 필터의 한 부분에서 검출 되면 높은 수를 남기고 그렇지 않으면 다른 최대값들에 비해 상대적으로 작아져 특징을 더 잘 남길 수 있음
평균 풀링
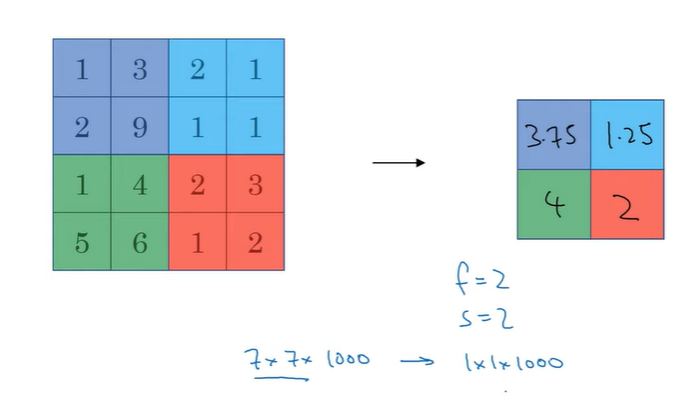
- 최대값을 취하는 대신 각 필터의 평균을 취함
- 최대 풀링이 평균 풀링보다 훨씬 더 많이 사용
Summary of pooling
Hyperparameters
- f: filter size
- s: stride
- 일반적인 선택: f=2, s=2
- 높이와 너비를 절반으로 줄여주는 효과가 있음
- 최대 풀링에서는 패딩을 거의 사용하지 않음
-> p=0 - 학습하는 변수가 없음
- x x
-> x x
10. CNN 예시
Neural network example
-
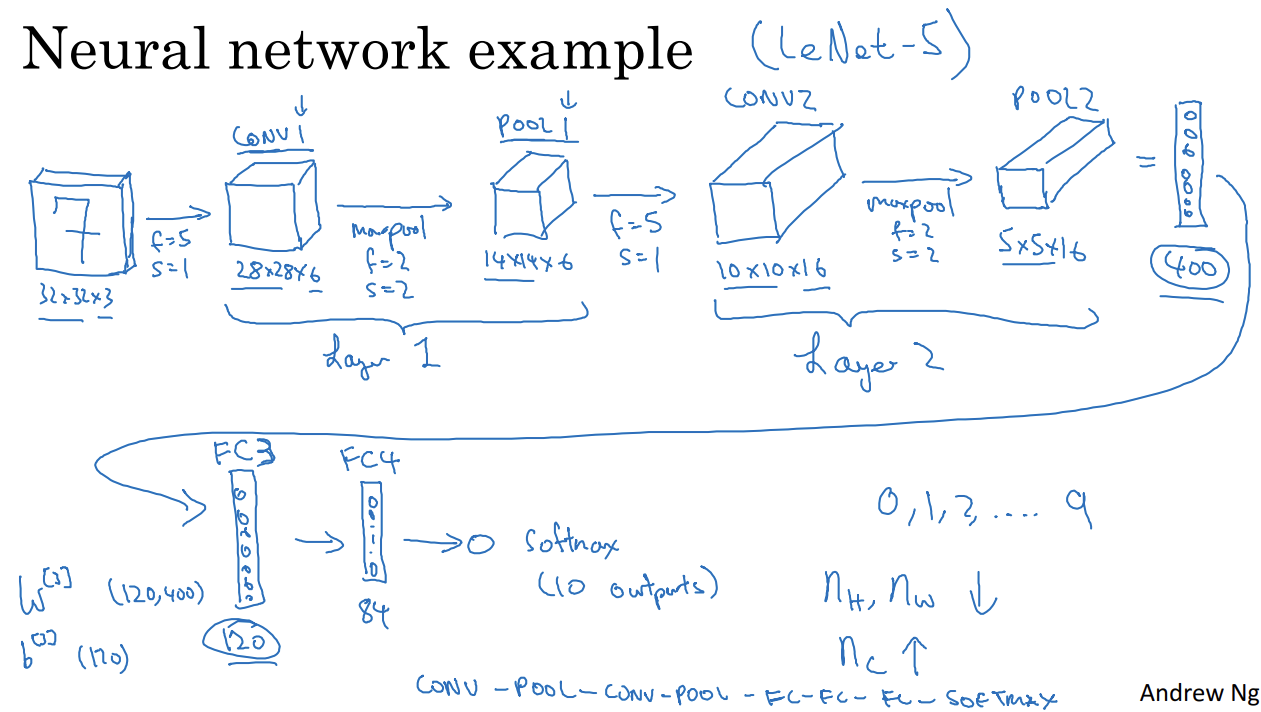
LeNet-5라는 사용한 고전적인 신경망과 유사한 구조
-
Layer1
- Layer1=CONV1+POOL1
- CONV1: 6개 필터, 편향 적용, ReLU 비선형성
- 최대풀링: f=2, s=2 -> 높이, 너비의 값 절반
- POOL1: 14x14x6
-
Layer2
- CONV2+POOL2
- POOL2: 5x5x16
-
POOL2를 400x1 유닛을 이용해 120개의 유닛으로 만들어주기 -> FC3
-
84개의 유닛 -> FC4
-
softmax 유닛에 적용
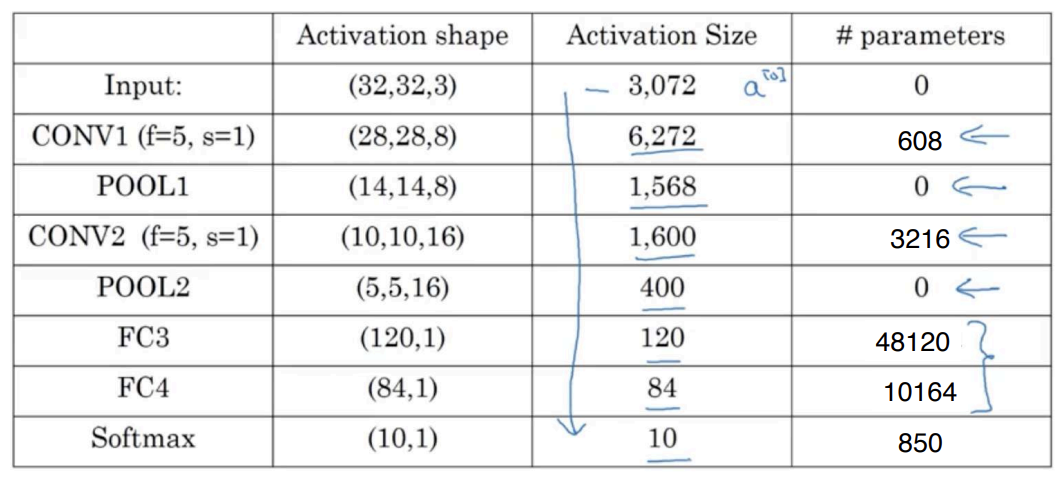
-
하이퍼 파라미터 선정: 직접 선정하지 말고 다른 사용자들에게 작동했던 하이퍼 파라미터를 보고 자신의 프로그램에도 잘 작동할 구조 선택
-
높이와 너비는 감소/채널의 수는 증가
-
활성값의 크기도 신경망이 깊어질수록 점점 감소
- 너무 빠르게 감소한다면 성능이 좋지 않을 수 있음
11. 왜 합성곱을 사용할까요?
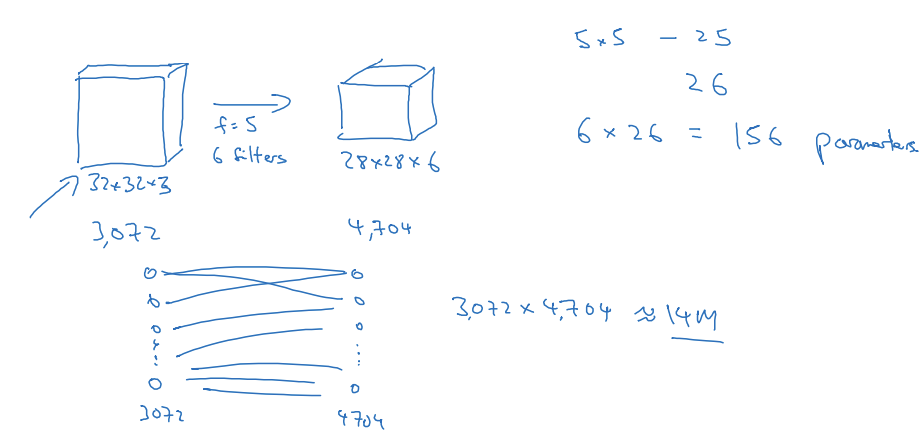
- 일반적인 신경망으로는 3,072 x 4,704 + 4,704, 약 1400 만개의 변수가 필요
- 32 x 32 x 3 이미지를 5 x 5 필터 6개를 통해 28 x 28 x 6 의 이미지로 합성곱 연산을 했을 경우, 필요한 변수의 개수는 26 x 6 = 156
-> 합성곱 신경망을 사용하면 변수를 적게 사용할 수 있음
2가지 이유
- 변수 공유
어떤 한 부분에서 이미지의 특성을 검출하는 필터가 이미지의 다른 부분에서도 똑같이 적용됨 - 희소 연결
출력값이 이미지의 일부(작은 입력값)에 영향을 받고, 나머지 픽셀들의 영향을 받지 않기 때문에, 과대적합을 방지할 수 있음
해당글은 부스트코스의 [딥러닝 4단계] 1. 합성곱 신경망 강의를 듣고 작성한 글입니다.