수리통계학 2강 - 확률집합함수 ~ 조건부 확률과 확률적 독립성

Thm 1.3.4

$0\le P(C)\le1, \ \forall c \in B$
$0=P(\phi) \le P(c) \le P(C) = 1$

Thm 1.3.5

$P(C_1 \cup C_2) = P(C_1) + P(C_2) - P(C_1 \cap C_2)$

$P(C_1 \cup C_2) = P(C_1) + P(C_1^c \cap C_2)$ $\cdot\cdot\cdot (1)$

$C_2 = (C_1 \cap C_2) \cup (C_1^c \cap C_2)$

$P(C_2) = P(C_1 \cap C_2) + p(C_1^c \cap C_2)$ $\cdot\cdot\cdot (2)$
(1) - (2) -->
$P(C_1 \cup C_2) - P(c_2) = P(C_1) - P(C_1 \cap C_2)$

Remark 1.3.1 ($Inclusion - exclusion\ formular$)

$P(C_1 \cup C_2 \cup C_3) = P_1 - P_2 + P_3$
$P_1 = P(C_1) + P(C_2) + P(C_3)$
$P_2 = P(C_1 \cap C_2) + P(C_1 \cap C_3) + P(C_2 \cap C_3)$
$P_3 = P(C_1 \cap C_2 \cap C_3)$

In general,

$P(C_1 \cup C_2 \cup C_3 \cup \cdot\cdot\cdot C_k) = P_1 - P_2 + P_3 - \cdot\cdot\cdot +(-1)^{k-1}P_k$
$p_i : sum\ of\ all\ possible\ intersection\ of\ i\ sets$
*$C_2, C_3 \cdot\cdot\cdot: Mutually\ exclusive$

$Mutually\ exclusive\ sets\ C_1, C_2, \cdot\cdot\cdot are\ called$ Exhaaustive(만약 $C_k$의 합이 표본공간인 경우)

* $\lim_{n\to\infin}C_n$을 쓸 수 있는 특수한 경우

(1) Countable union and Increasing sets

$\bigcup_{n=1}^\infin C_n,\ C_i's:increasing\ set(C_1 \subset C_2 \subset C_3\ \cdot\cdot\cdot\cdot)$

(2) Countable union and Decreasing sets

$\bigcap_{n=1}^\infin C_n,\ C_i's:decreasing\ set(C_1 \supset C_2 \supset C_3\ \cdot\cdot\cdot\cdot)$

ex) $C_n =$ {${x: 0 < x < 1- {1 \over (n+1)}}$}
ex) $C_n =$ {${x: 0 < x < 1+ {1 \over (n+1)}}$}

Thm 1.3.6

{$C_n$}: increasing set
$\lim_{n \to \infin}P(C_n)$ := $P(\lim_{n \to \infin} C_n)$
pf)

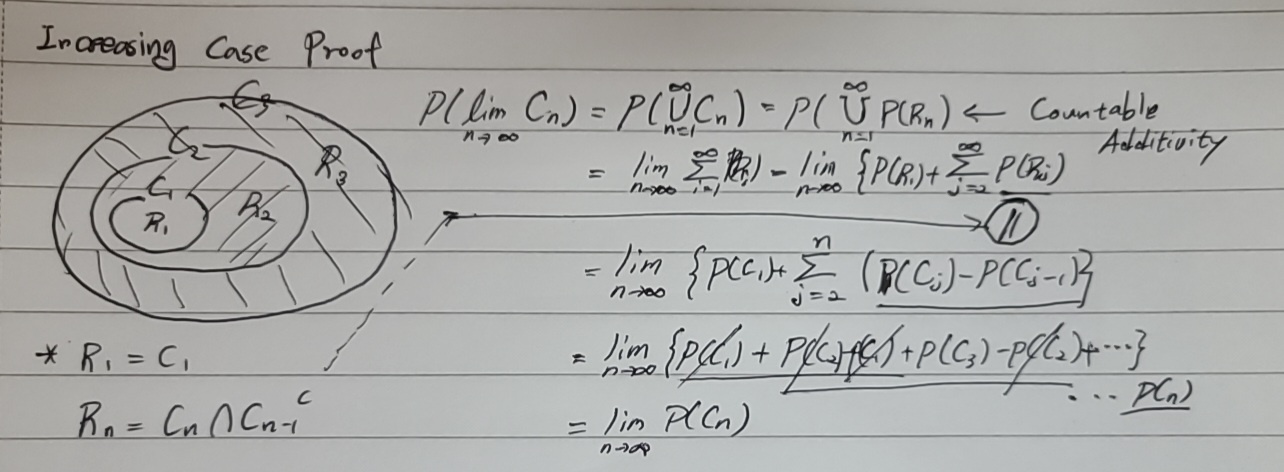
{$C_n$}: decreasing set
$\lim_{n \to \infin}P(C_n)$ := $P(\lim_{n \to \infin} C_n)$

Thm 1.3.7(Boole's inequality)

{$C_n$}: arbitrary seg of sets
$P(\bigcup_{n=1}^ \infin C_n) \le \sum_{n=1}^ \infin P(C_n)$

1.4 조건부확률과 독립성(Conditional Prob & Independence)

$C_1, C_2 \in C$,
The conditional probability of $C_2$ given $C_1$
$P(C_2 \mid C_1)$ := $P(C_2 \cap C_1) \over P(C_1)$
$*P(C_1) \ne \phi$
(1) $P(C_2 \mid C_1) \ge 0 (non-negativity)$
(2) $P(C_2 \mid C_2) = 1 (Normality)$
(3) $C_2, C_3, C_4, \cdot\cdot\cdot: mutually\ exclusive$

-->$P(\bigcup_{i=1}^ \infin C_i \mid C_1)= \sum_{i=1}^ \infin P(C_i \mid C_1)$ <- countable additivity

ex1.4.1
포커 카드(52장)에서 비복원 추출 시, 6번째 뽑았던 것이 3번째 스페이드인 확률

--> 처음 5개 중 2개의 스페이드 출현
--> 마지막에 스페이드 출현

$C_1: two\ spades\ in\ the\ first\ five\ draws$
$C_2: third\ spades\ in\ the \ sixth\ draws$
$what\ is\ P(C_1 \cap C_2)?$
--> 교집합을 구하기 쉽지 않으니, 조건부확률로 구하자

$P(C_2 \mid C_1)$ := $P(C_2 \cap C_1) \over P(C_1)$ >>> $P(C_1 \cap C_2) = P(C_2 \mid C_1)$ *$P(C_1)$

(1) $P(C_2 \mid C_1)$는 52개의 카드 中 5개를 뽑았는데 2개의 스페이드가 나온 상황에서 또 6번째로 스페이드를 뽑을 확률

($P(C_2 \mid C_1)$ = $(13-2) \over (52-5)$ -> 47개의 패 중에서 스페이드를 뽑을 확률)

(2) $P(C_1)$는 5개 뽑았는데 2개가 스페이드일 확률
$P(C_1) =$ ${}_{13}{\rm C}_{2} \over {}_{52}{\rm C}_{5}$

(1) * (2) = 0.064

Joint Prob을 Marginal Prob과 Conditional Prob의 곱으로 나타내기

$P(C_1 \cap C_2) = P(C_1)*P(C_2 \mid C_1$)

$P(C_3 \mid C_1 \cap C_2) =$ $P(C_3 \cap C_2 \cap C_1) \over P(C_1 \cap C_2)$

$P(C_3 \cap C_2 \cap C_1)$ = $P(C_1 \cap C_2)*P(C_3 \mid C_1 \cap C_2)$

In general,
$P(C_1 \cap C_2 \cap C_3 \cdot\cdot\cdot)$
= $P(C_1)*P(C_2 \mid C_1)*P(C_3 \mid C_1 \cap C_2) \cdot\cdot\cdot$

Bayes Theorm

$C_1, C_2, C_3 \cdot\cdot\cdot$: mutually exclusive & exhaustive
$P(C_i) > 0, \forall i = 1, \cdot\cdot\cdot , k$

$P(C_j \mid C)$ = ${P(C_j)*P(C \mid C_j)} \over {\sum_{i=1}^k P(C_i)*P(C \mid C_i)}$

• 좌변이 구하기 어려운 경우이거나 비현실적인 경우, 우변을 통해 우회하여 구하는 것
  pf)

Remark 1.4.1 베이지안 기초 용어

• $P(C_j): Prior\ prob$(사전확률)
• $P(C_j \mid C): Posterior\ prob$(사후확률)

Def 1.4.1 독립의 정의(왜 독립인 두사건의 교집합은 곱으로 나타내는가)

$C_1, C_2: (Statistical)\ independent\ iff$
$P(C_1 \mid C_2) = P(C_1)$

In general,
$C_1, C_2, \cdot\cdot\cdot independent$
iff every collection of k event(2 $\le k \le n$)
$P(C_{i1} \cap C_{i2} \cdot\cdot\cdot \cap C_{ik})$ = $\prod_{j=1}^k P(C_{ij})$

cf)
$C_i,C_j: pairwise\ independent\ if$
$P(C_i \cap C_j) = P(C_i)P(C_j),\ \forall i \ne j$