정렬별 시간복잡도

• 시간복잡도 표는 링크 참고
• $O(N^2)$
  • bubble
  • selection
  • insert
• ${O(NlogN)}$
  • Quick (최악의 경우엔 $O(N^2)$)
  • Merge
  • Heap

• 빠른 것 만이 좋은 것이 아니다!
  • 정렬 index 가 0...N 이라면,
  • 선택정렬은 'i' 번째에 왔다면, '0'~'i-1' 번째까지 내 앞까지 정렬됨을 보장한다.
  • 버블정렬은 'i' 번째에 왔다면, 'i+1'~'N'까지 뒷정렬을 보장한다.

---

selection sort

• 선택 정렬
• $O(N^2)$
• 장점
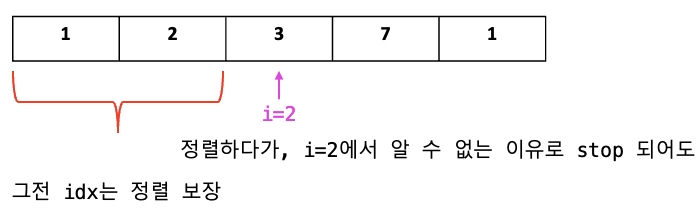
  • 정렬하다 i번 째에서 멈춰도, 그 '앞' 까진 정렬 보장
    
  • 2 번째 큰수, 만 구하라 때 아주 유용할 수 있다.
    • ${>}$ 내림 차순 으로 정렬해서, 2번째까지 값만 구하면 된다.
      • e.g., Quick sort가 ${O(NlogN)}$ 이지만 '${N=10K}$' 라고 가정 시,
        Quick sort: ${O(10K log 10*10^3)}$ = ${O(40K)}$
        Selection sort 2번째까지 하고 멈춤: ${O(2*N)}$ = ${O(20K)}$

---

Big O

• 전체 정렬일 경우 ${O(N*N = N^2)}$
  

---

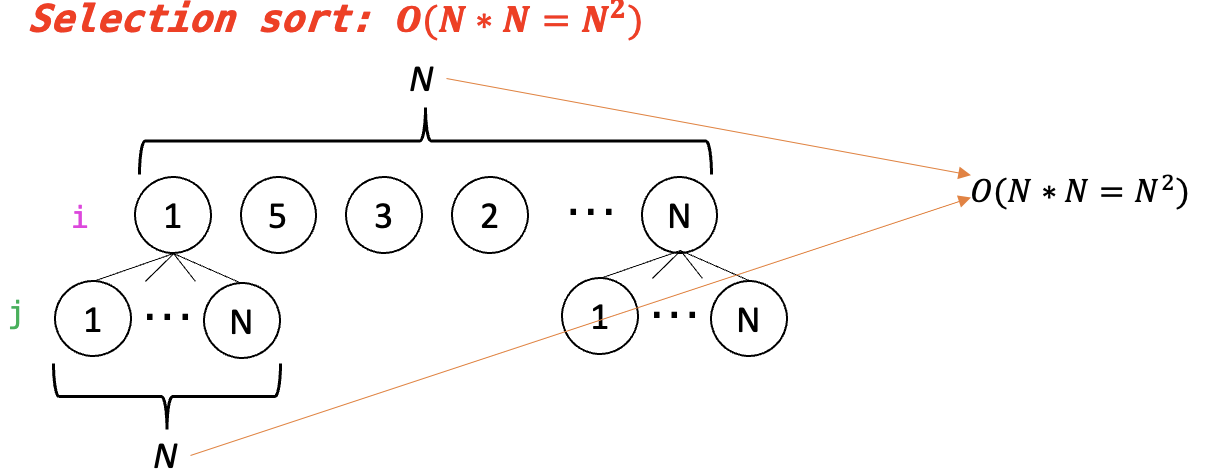
• Selection Sort를 상위 2개만 한다고 가정한다. 이는 ${O(2 * N)}$
  

---

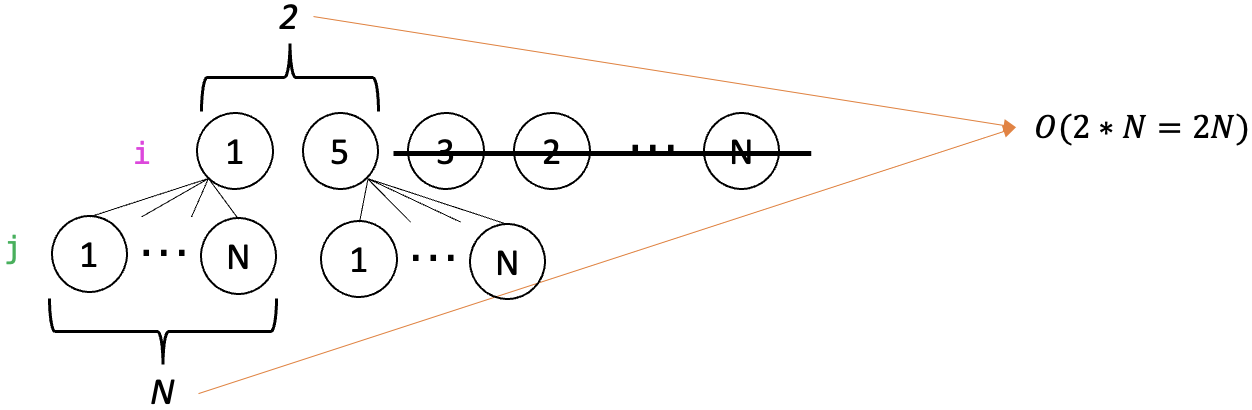
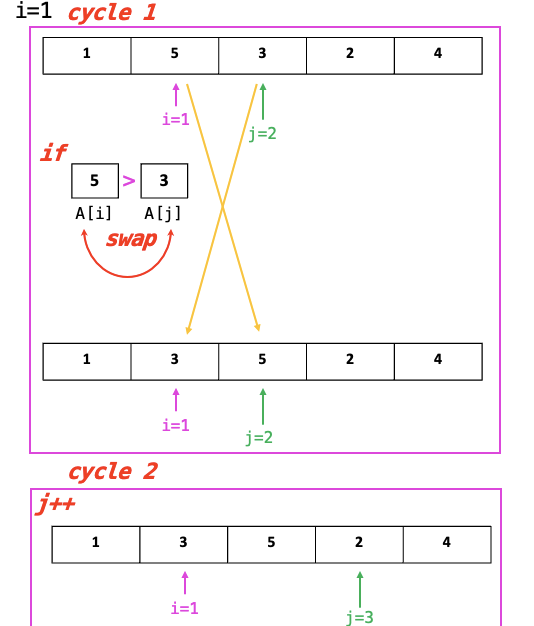
• selection sort의 오름차순(ascending) 정렬 ${＜}$
  
  

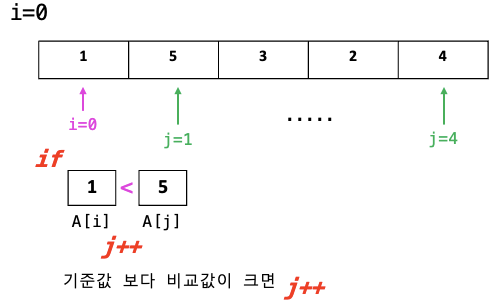
1. A[i], A[j]를 비교하면서, 나보다 작은 element (A[i] ＞ A[j]) 발견시 swap!
   하나의 데이터를 선택해 나머지와 비교하면서, 작은 데이터가 나타나면 위치 교환
2. swap 후, j+1부터 다시 서칭
   
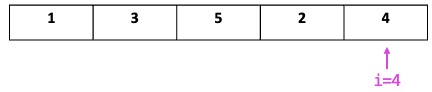
3. i == N-1 도착 시 종료
   

---

Ascending

import sys

def ascending_sort(N:int, A:list):
    for i in range(0,N):
        if i == N-1:
            break
        for j in range(i+1,N):
            if A[j]>A[i]:
                continue
            else:
                temp=A[i]
                A[i]=A[j]
                A[j]=temp

if __name__ == '__main__':
    readl=sys.stdin.readline
    N=int(readl())
    A=list(map(int,readl().split()))
    ascending_sort(N,A)
    print(*A)

---

Descending

import sys

def descending_sort(N: int, A: list):
    for i in range(0, N):
        if i==N-1:
            break
        for j in range(i+1, N):
            if A[i]<A[j]:
                temp=A[i]
                A[i]=A[j]
                A[j]=temp
            else:
                continue

if __name__ == '__main__':
    readl=sys.stdin.readline
    N=int(readl())
    if N == 0:
        exit(0)
    A=list(map(int,readl().split()))
    descending_sort(N,A)
    print(*A)

---

작은 수 '4개'만 보자!

• selection sort의 진가인 i 번째까진 보장
  • 전체 정렬: ${O(N^2)}$
  • 작은 수 4개만 보자!: ${O(4*N)}$

• 작은 수 4개니까 당연히, ascending sort 해야겟지?

import sys
GET_NUMS=4 # How many numbers that you want to get it from Array A, in your standard.

def ascending_sort(N:int, A:list):
    for i in range(0,N):
        if i == N-1:
            break
        if i == GET_NUMS: # i Cycle을 i가 index 4에 도착하면 끊으면 됨
            break
        for j in range(i+1,N): # 훑어 보기는 전부 봐야함
            if A[i] > A[j]:
                temp=A[i]
                A[i]=A[j]
                A[j]=temp
            else:
                continue

if __name__ == '__main__':
    readl=sys.stdin.readline
    N=int(readl())
    A=list(map(int,readl().split()))
    ascending_sort(N,A)
    print(*A[0:GET_NUMS])

---

높은 수 3개, Priority 有

• 높은 수 3개 찾기
  1. Descending sort
  2. $>$
  3. 교환 조건
     3.1.

import sys

# Find 'GET_NUMS' Upper Nums
GET_NUMS=3

def descending_sort(N: int, A: list):
    for i in range(0,N):
        if i == N-1:
            break
        if i == 3:
            break
        for j in range(i+1,N):
            if (A[i][0] < A[j][0]) or (A[i][0] == A[j][0] and A[i][1] > A[j][1]):
                temp=A[i]
                A[i]=A[j]
                A[j]=temp
        
if __name__ == '__main__':
    readl=sys.stdin.readline
    N=int(readl())
    A=list(map(int,readl().split()))
    A_len=len(A)
    for i in range(0,A_len):
        A[i]=(A[i],i+1)
    descending_sort(N,A)
    for i in range(0,GET_NUMS):
        print(A[i][1],end=' ')

---

Quick sort

• Divide & Conquer 방식 Algorithm 사용
• 시간복잡도: Average ${O(NlogN)}$, worst $O(N^2)$

---

Ascending

• Quicksort Ascending ＜
• 하나의 Pivot을 정함
  • Pivot은 구현에 따라 'idx: 0', 'idx: 2/N', 'idx: N'이 될수 있음
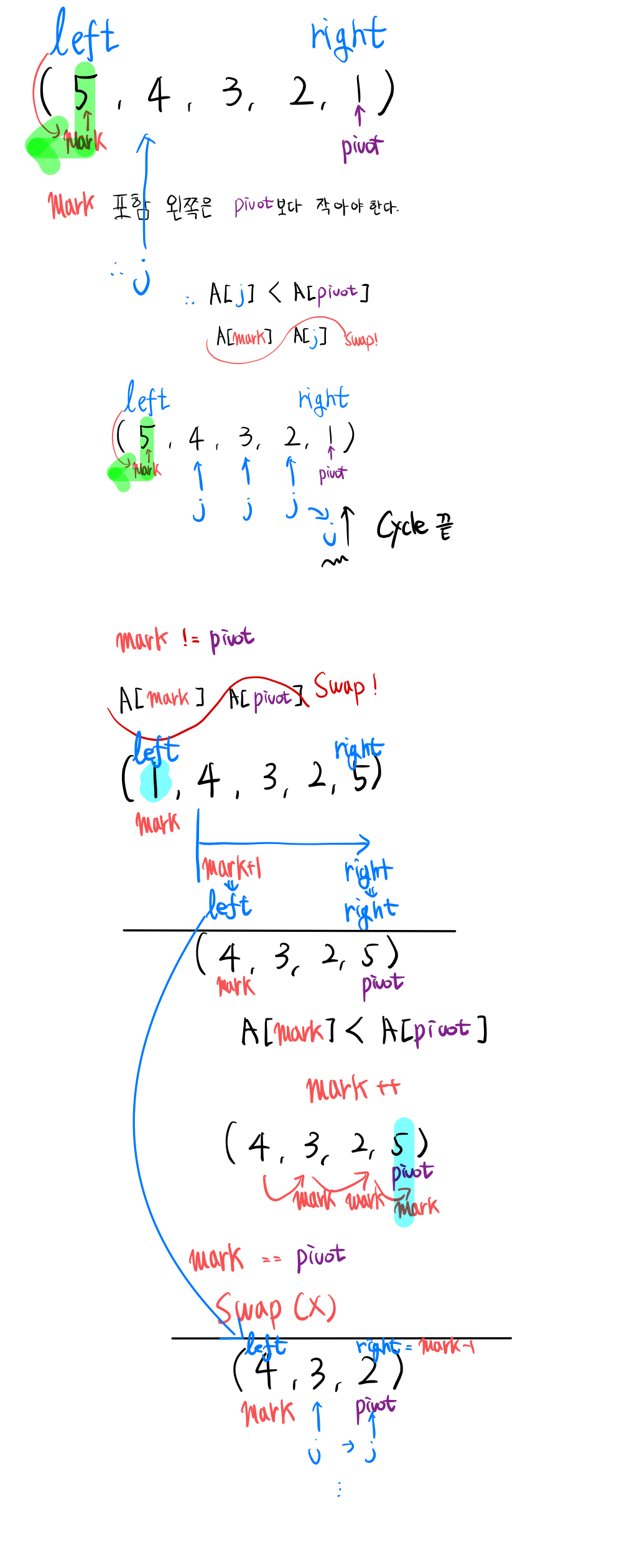
• mark를 i=0설정
  

---

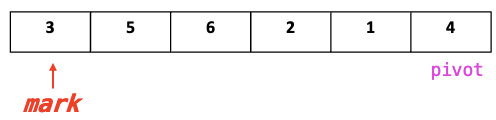
• Point!

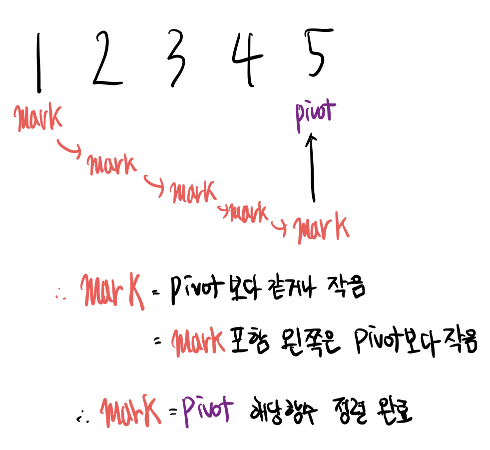
1. mark 포함 왼쪽 idx 들은 ＜ Pivot 값

---

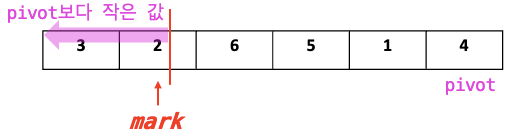
2. if 　 j ＜ pivot 　: 　mark ＜＝＞ j 　Swap!

---

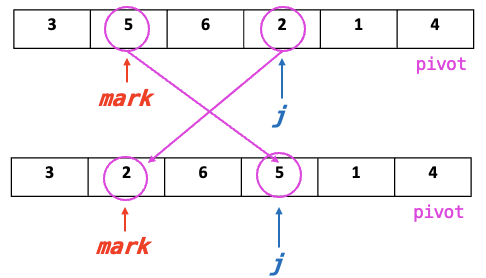
3. Swap 후엔, mark++

---

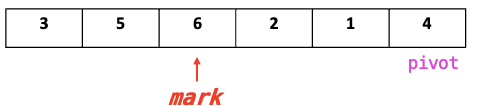
4. mark > Pivot, j = mark+1, finding j ＜ pivot
   but, j위치 = Pivot 위치, then mark ＜=＞ j 　Swap!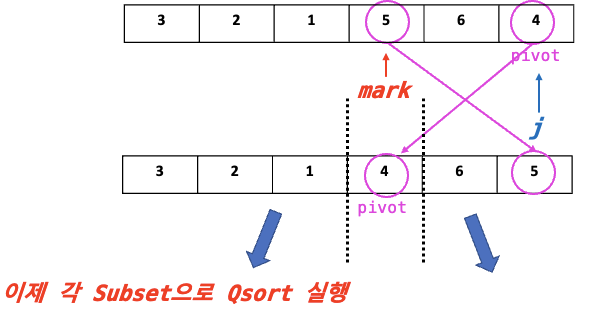
   4-1. 여기서 결정된 '4'는 정말 앞에서 4번째 위치임. 옮겨진 pivot 왼쪽, 오른쪽은 정렬 X지만 확실한 것은
   왼쪽 ＜ pivot ＜ 오른쪽

---

5. 최악의 경우

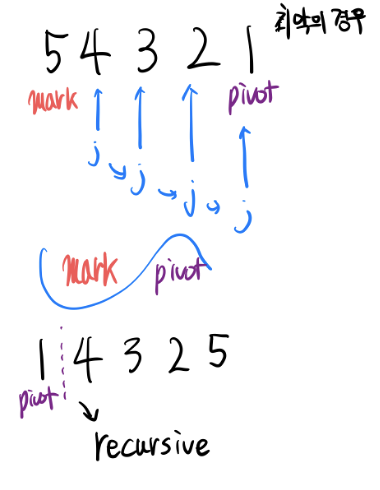
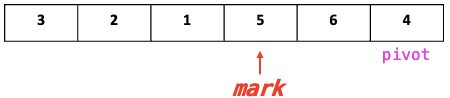
• mark == pivot 이라는 의미는, mark는 pivot보다 같거나 적고, mark 포함 왼쪽 전부 pivot 보다 같거나 작은 상태. 즉, 해당 함수 정렬 완료

---

scenario 1.

Scenario

1. mark < Pivot
   1.1. mark++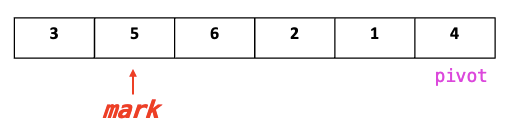

---

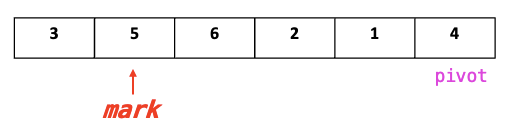2. mark > Pivot
   2.1. j = mark+1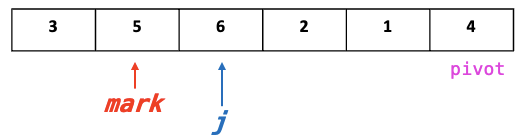
   2.2. if 　 j ＞ pivot 　: 　j++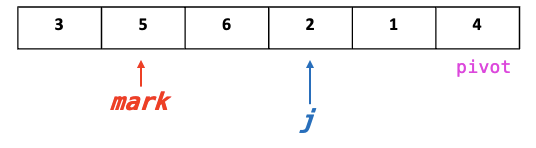

---

3. if 　 j ＜ pivot 　: 　mark ＜=＞ j 　Swap!
   3.1. mark++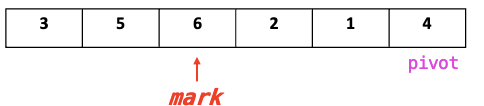

---

4. mark > Pivot
   4.1. j = mark+1
   
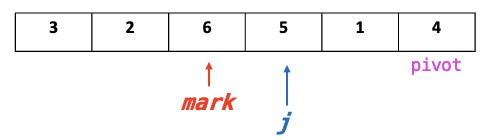
   4.2. finding j ＜ pivot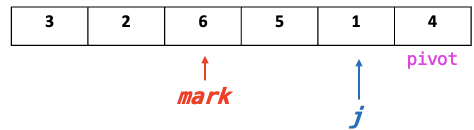
   4.3. swap
   
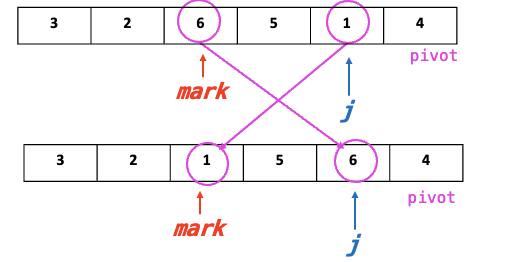
   4.4. mark++
   

---

5. mark > Pivot, j = mark+1, finding j ＜ pivot
   but, j위치 = Pivot 위치, then mark ＜=＞ j 　Swap!

---

scenario 2.

---

Code

import sys

N=None
A=None

def q_sort(left: int, right: int):
    if left >= right:
        return
    P=right
    mark=left
    for j in range(mark, P):
        if A[j] < A[P]:
            if j != mark:
                temp=A[mark]
                A[mark]=A[j]
                A[j]=temp
            mark+=1

    if P != mark:
        temp=A[P]
        A[P]=A[mark]
        A[mark]=temp
    q_sort(left,mark-1)
    q_sort(mark+1,right)

if __name__ == '__main__':
    readl=sys.stdin.readline
    N=int(readl())
    A=list(map(int,readl().split()))
    q_sort(0,N-1)
    print(*A)

---

Priority 2개

1. Priority1: Value
2. Priority2: 들어온 순서

---

• 기존 mark ＜＝＝swap＝＝＝＞ j

    for j in range(mark, P):
        if A[j] < A[P]:
            if j != mark:
                temp=A[mark]
                A[mark]=A[j]
                A[j]=temp
            mark+=1

---

• 2개의 Priority 고려시
  1 순위: Value 가 낮을 수록 (오름차순)
  2 순위: Value가 같을 때, 들어온 순서 (ID가 낮을 수록)

   for j in range(mark, P):
       if (A[j][0] < A[P][0]) or ((A[j][0] == A[P][0]) and (A[j][1] > A[P][1])):
           if j != mark:
               temp=A[mark]
               A[mark]=A[j]
               A[j]=temp
           mark+=1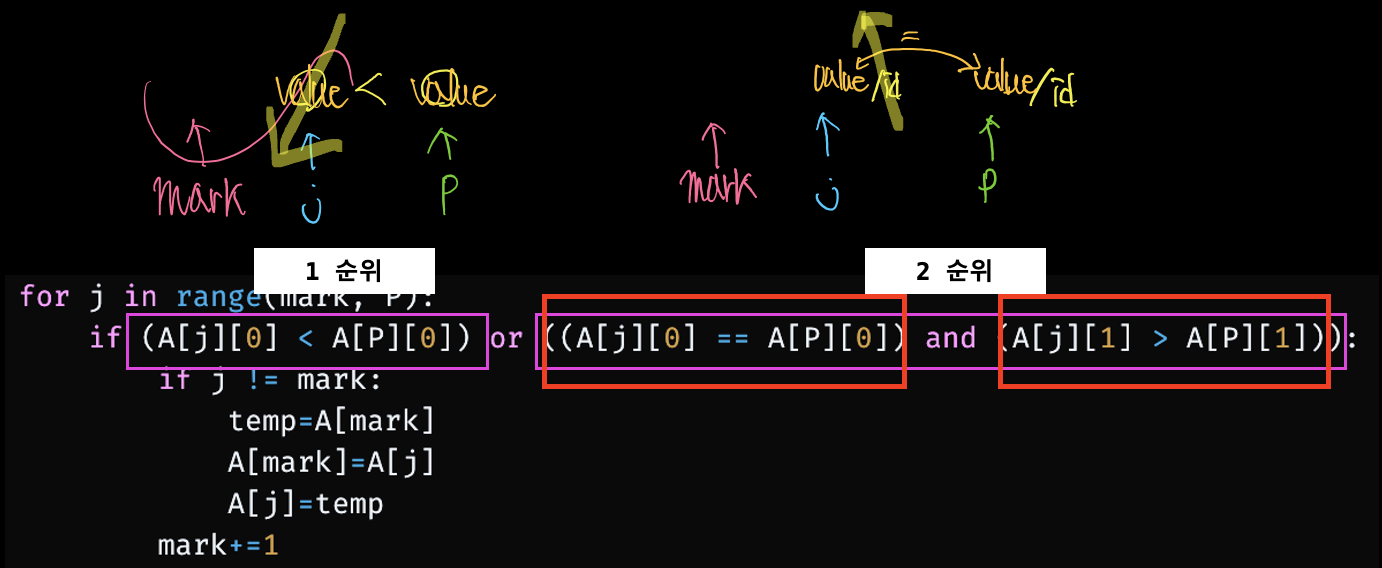

구현 시에는 Priority와 반대 부호임

---

merge sort (Devide and Qonquer)