"프로그래머를 위한 확률과 통계" 책과 스터디 내용을 기반으로 작성하였습니다.

---

2.1 확률변수의 조합

1) 결합확률과 주변확률의 연습

• 배반 사건: 동시에 발생할 수 없는 사건 ex) 홀수와 짝수
• 독립 사건: 서로 영향을 주지 않는 사건 ex) 2번의 동전 던지기

결합확률

• 서로 다른 두 사건이 동시에 발생할 확률

주변확률

• 결합되지 않는 개별 확률
• 하나의 나라(모집단) 면적을 1이라고 할 때, 나라의 도시 A, B, C가 있다고 가정
• 나라의 토지는 공장, 주택, 논밭으로 구성
• P(A) + P(B) + P(C) = 1 : 주변 확률
• P(주택) + P(공장) + P(논밭) = 1 : 주변 확률
• P(논밭) = P(A $\cap$ 논밭) + P(B $\cap$ 논밭) + P(C $\cap$ 논밭) : 결합 확률
• P(A) = P(A $\cap$ 논밭) + P(A $\cap$ 공장) + P(A $\cap$ 주택) : 결합 확률

2) 조건부 확률의 연습

조건부 확률

• 한 사건이 발생한 경우 다른 사건이 발생할 확률
  ex) 도시 A에서의 공장면적 확률: P(공장|A)
• P(공장|A) + P(논밭|A) + P(주택|A) = 1 (* 총 면적이 1인 것과는 다릅니다.)
• P(공장|A) = $\frac {P(공장 \cap A)} {P(A)}$
• 주의!
  • P(공장|A) + P(공장|B) + P(공장|C) $\neq$ 1
  • 분모가 다르기에 1이 넘어갈 수도 있습니다.

3) 비율의 역산 (베이즈 공식 훈련)

• P(시/도)와 P(용도|시/도)를 바탕으로 P(시/도|용도)를 구할 때 사용
  ex) P(A|공장)를 알고 싶을 경우

• P(A|공장) = $\frac {P(A \cap 공장)} {P(공장)}$
• P(A $\cap$ 공장)와 P(공장)를 알면 해결됩니다.

4) 비율이 획일적인 경우 (독립성 훈련)

• if 모든 시/도가 동일한 비율로 용도별 면적을 나누었다면
• == if 시/도 에 상관없이 용도별 비율이 일정합니다. 다른 사건의 영향을 받지 않습니다.
• 따라서 독립사건이라고 할 수 있습니다.
• 이때 P(A $\cap$ 공장) = P(A) * P(공장)이 성립합니다.
• 반대의 경우도 가능합니다.
• if 모든 용도별에 따라 시/도가 동일한 비율이라면 위와 같은 결과를 보입니다.

---

2.2 결합 확률과 주변 확률

1) 두 개의 확률 변수

예제 1)

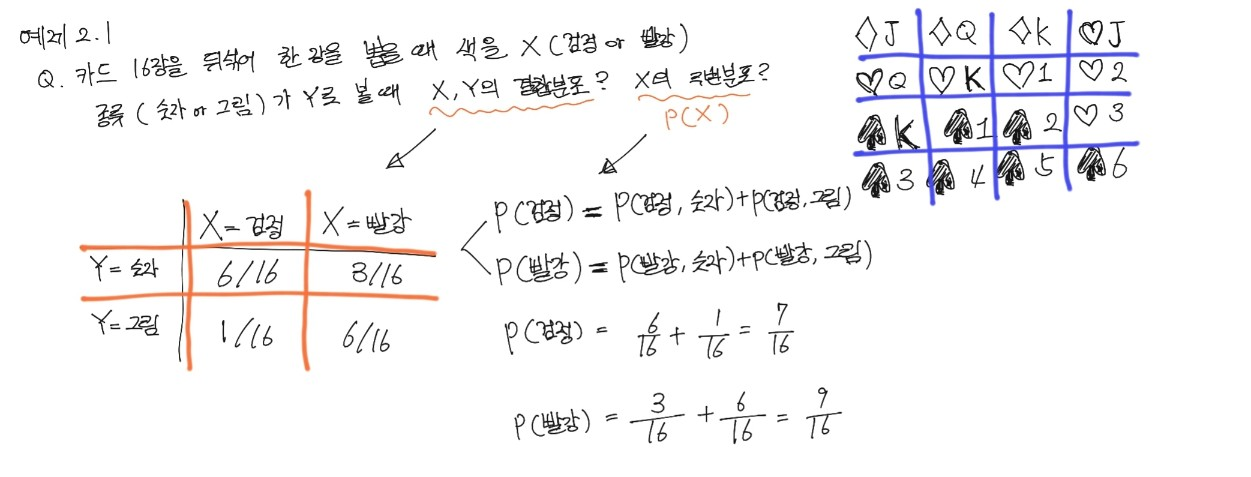
예제 2)

---

2.3 조건부 확률

1) 조건부 확률

• 주어진 조건 하에 다른 사건이 발생할 확률
• 일반적인 정의

$P(Y=b|X=a)=\frac {P(X=a, Y=b)} {P(X=a)}$

• 성질
  $\sum_{b} P(Y=b|X=a)=1$
  $\sum_{a} P(Y=b|X=a)\neq1$ (무조건적인 1이 아니다.)

2) 결합 분포, 주변 분포, 조건 분포의 관계

• $P(X=a)=\sum_{b}P(X=a, Y=b)$
• $P(Y=b)=\sum_{a} P(X=a, Y=b)$
• $P(X=a, Y=b)$
  $=P(X=a|Y=b)*P(Y=b)$
  $=P(Y=b|X=a)*P(X=a)$
• $P(X=a, Y=b, Z=c)$
  $= P(X=a|Y=b,Z=c)*P(Y=b|Z=c)*P(Z=c)$

몬티 홀 문제에 적용(다 문이 정답일 경우)

• A: 정답 문
• B: 도전자가 선택하는 문
• C: 진행자가 여는 문
• $P(A="다"|B="다", C="가")$
  $= \frac {P(X="다", Y="다", Z="가")} {P(Y="다", Z="가")}$

---

2.4 베이즈 공식

조건부 확률의 응용

---

2.5 독립성

1) 독립성이란

• 각자 영향을 받지 않는 성질(=항상 일정)

2) 독립성 조건(조건과 조건의 독립성)

• A와 B는 서로 독립 사건입니다.
• 조건부 확률의 조건에 따른 확률이 변하지 않습니다.
  P(A|B) = P(A|B$^{c}$)
• 조건의 존재 여부에 따라서도 변하지 않습니다.
• 결합 확률의 비율이 같습니다.
  P(A, B) : P(A, B$^c$) = P(A$^c$, B) : P(A$^c$, B$^c$)
• 결합확률이 주위확률의 곱입니다.
  P(A, B) = P(A)*P(B)
• A와 B의 역할을 바꾸어도 동일합니다.

3) 확률 변수의 독립성

확률변수의 독립성

어떤 값 a, b에 대하여 조건 X=a와 조건 Y=b가 항상 독립할 때 확률변수 X, Y는 독립이라고 합니다.

• X와 Y가 독립
• 조건부분포가 조건에 따르지 않습니다.
  • P(Y=b|X=a)는 a에 의존하지 않고 b만으로 정해집니다.
• 조건을 달고도 연결된 분포가 바뀌지 않습니다.
  • P(Y=b|X=a)=P(Y=b)가 항상 성립합니다.
• 결합확률의 비가 일정합니다.
  • P(X=a, Y=b) : P(X=a, Y=c) = P(X=d, Y=b) : P(X=d, Y=c)
• 결합 확률이 주변 확률의 곱입니다.
  • P(X=a, Y=b) = P(X=a)*P(Y=b)
• X와 Y를 바꾸어도 동일합니다.

4) 세 개 이상의 독립성(중요)

• (코끼리, 개미, 사람, ___) 카드가 있을 때 이 중 하나만 고른다면 독립인 사건입니다.
• 두 개의 사건의 경우 모두 독립으로 보이지만 두 조건을 알면 나머지도 유추할 수 있습니다.
• 각각의 짝이 독립이라고 하여도 전체가 독립이라고 보기는 어렵다는 이야기 입니다.
• 조건의 여부에 따른 확률변화 X
  
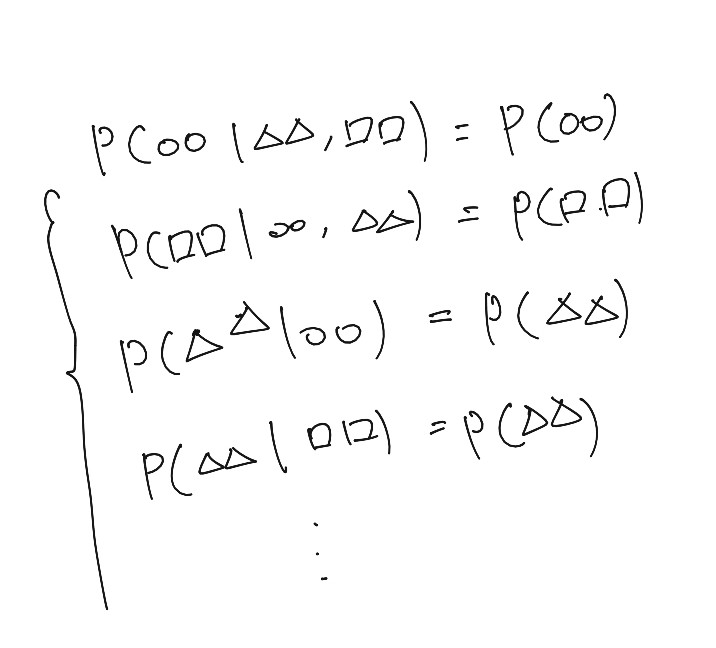
• 결합확률과 주변 분포, 조건 분포와의 관계
  
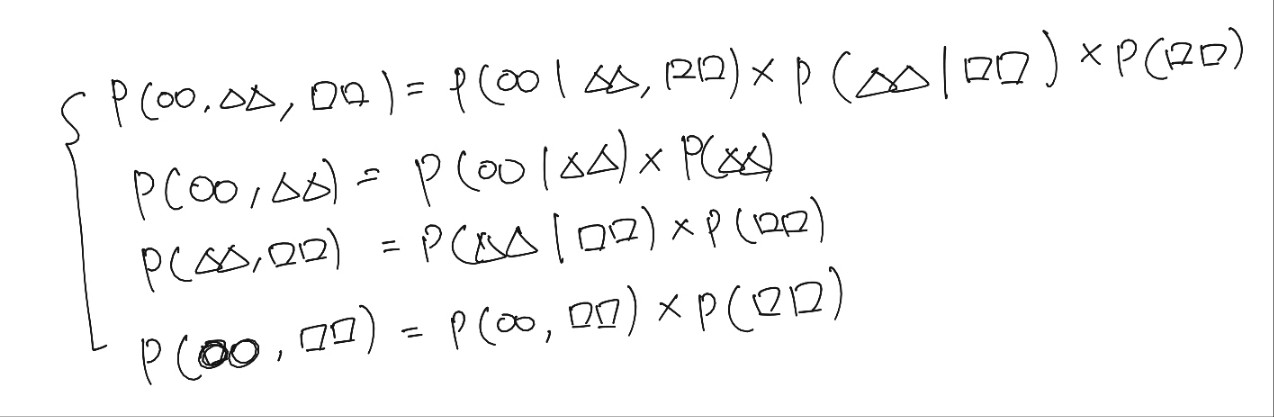
• 결합확률이 항상 주변확률의 곱인 경우
  
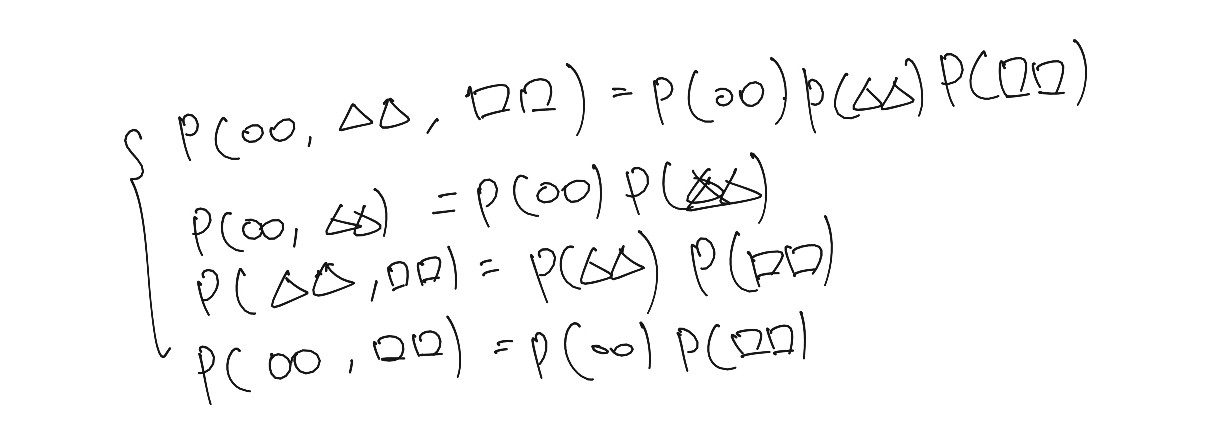
• 확률변수의 경우도 동일합니다.