"프로그래머를 위한 확률과 통계" 책과 스터디 내용을 기반으로 작성하였습니다.

---

3.1 일반 이산값

• 이산값: 수치적인 의미를 가지며 소수점의 형태가 아닌 구분되는 값, 무한하지만 셀 수 있는 값
• 균등분포: 각각의 확률이 일정하며 확률의 합이 1이 되는 분포
• 순열: 서로 다른 n개 중 k개를 뽑아 나열하는 것: $_{n}\mathrm {P}_{k}=\frac {n!} {(n-k)!}$
• 조합: 서로 다른 n개 중 순서에 상관없이 k개를 뽑는 것: $_{n} \mathrm{C}_{k} = \frac {_{n} \mathrm {P}_{k}} {k!} = \frac {n!} {k! * (n-k)!}$

---

3.2 이항분포

• 베르누이 시행

  • 두 가지 결과값만 가지는 실험결과를 의미하며 각각의 결과를 성공과 실패로 정의합니다.
    ex) 동전 던지기 등
  • 각 실험은 독립적으로 시행됩니다.
  • 모든 실험의 결과에서 확률은 항상 동일합니다.

• 이항분포

  • 연속된 n번의 독립적인 시행에서 각 시행이 p확률을 가질 때의 이산확률분포

  • 시행 횟수와 공통적인 확률에 따라 분포의 모습이 바뀝니다.
    

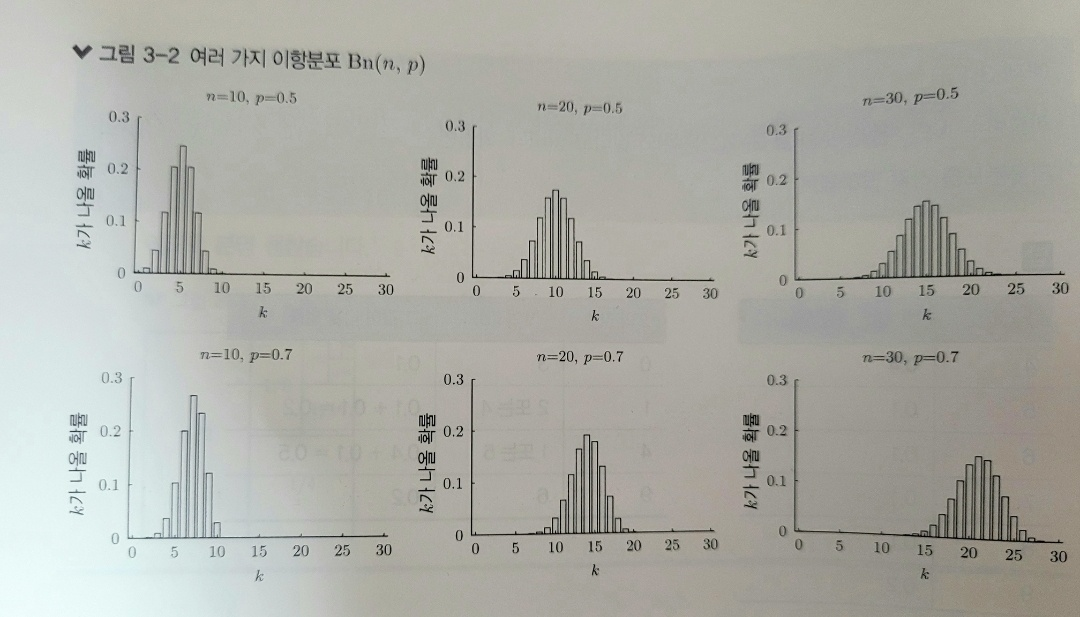
  • Bn(n, p)
    i) 동전 던지기 7번에서 앞면(p)이 3번 나타날 확률 -> $p^{3}q^{4}$
    ii) 7번 중 3번이 앞면일 패턴: $_{7} {C}_3$ = $\frac {7!} {3!* 4!}=35$
    iii) $P(X=3)$ = $35*p^3q^4$

---

3.3 기댓값

• 각 사건이 벌어졌을 때의 확률과 발생한 사건의 곱의 총합, 확률변수의 가중평균

• 동일한 사건 다른 확률에도 기댓값은 변하지 않습니다.

  • $E[x]$ = $\sum_{i=1}^{n}x_{i}p_{i}$

• 기댓값의 기본 성질

  • $a, b \in \mathbb {R}$, 확률변수 X, Y에 대해 다음과 같은 성질을 만족합니다.

    1. $E[aX+b] = aE[X]+b$
    2. $E[X+Y] = E[X] + E[Y]$
    3. $X > c$, $E[X] > c$
       *c는 상수
    4. $X, Y$가 독립, $E[XY] = E[X]*E[Y]$

• 기댓값이 존재하지 않을 경우

  • 무한대로 발산: 기댓값이 무한대가 나타날 경우가 있습니다.

    $P(X): \{\frac {1} {2}, \frac {1} {4}, \frac {1} {8}, ...\}$
    $Y: \{2, 4, 8, ...\}$
    $E(Y) = 1+1+1+...$

  • 무한 뻬기: 반대로 -1만 나타나기도 합니다.

---

3.4 분산과 표준편차

• 분산
  $V[X] = E[(X-u)^2]$
• 표준편차
  $\sigma = \sqrt {V[X]}$

1. $V[X+c]=V[X]$
2. $V[cX] = c^2V[X]$
3. X, Y가 독립, $V[X+Y] = V[X]+V[Y]$
4. $V[X]=E[X^{2}]-E[X]^{2}$

• 표준화
  • 분산과 표준편차를 통해 분포가 다른 두 데이터를 가지고 무엇인가를 하려고 할 때 사용합니다.

    $W = \frac {X-u} {\sigma}$

---

3.5 큰 수의 법칙

• 독립동일분포(i.i.d.)

  • 확률 각각의 분포가 모두 동일
  • 모두 독립적

• 평균값의 기댓값, 평균값의 분산

  • 평균(Z) = $\frac {X_{1}+X_{2}+ ... +X_{n}} {n}$

  • 평균값의 기댓값(E[Z]) = $\frac {E[X_{1}]+E[X_{2}]+...+E[X_{n}]} {n}$

  • 평균값의 분산(V[Z]) = $\frac {V[X_{1}+X_{2}+...+X_{n}]} {n^{2}}$

  + $X$가 독립인 경우

  • $E[X_{i}]=u$, $E[Z]$ = $\frac {n*u} {n}$ = $u$
  • $V[Z]$ = $\frac {V[X_{1}]+V[X_{2}]+...+V[X_{n}]} {n^2}$
  • $V[X_{i}]$ = $\sigma^{2}$, $V[Z]$ = $\frac {n \sigma^{2}} {n^{2}}$ = $\frac {\sigma^{2}} {n}$

• 큰 수의 법칙

  • $n$을 얼마든지 키울수 있다면 분산과 표준편차는 0에 가깝게 할 수 있습니다.
  • 또한 평균의 경우도 오차가 없어지며 기댓값 $u$에 수렴한다고 볼 수 있을 것입니다.

  ---

3.6 조건부 기댓값과 최소제곱 예측

1) 조건부 기댓값

• X가 a라는 관측값을 얻었을 때 Y를 예측하려면 조건부 확률 P(Y=b|X=a)에서 Y의 조건부 분포를 통해 구하는 기댓값

2) 최소제곱 예측

• 조건부 분포 P(Y=b|X=a)에서 X가 입력되었을 때 $\hat Y$인 Y의 전망값이 나타납니다.
• 이 때, 제곱오차 $(Y-\hat Y)^2$의 기댓값인 $E[(Y-\hat Y)^2]$를 가능한 작게 한다면
  $\hat Y$인 g(x)가 있을 때 $g(a)=E[Y|X=a]$ 입니다.

3) 조건부 분산

$E[Y|X=a]=u(a)$, $V[Y|X=a]=E[(Y-u(a))^{2}|X=a]$

• 분산의 정의에서 기댓값을 조건부 기댓값으로 변환하면 자연스럽습니다.