[23 하계 모각코] 1회차 - 분할 정복

이번주에는 2단원을 하는 것을 목표로 하였었고, 이에 따라 공부를 진행하였다.

1. Master Theorem

이건 분할 정복 알고리즘의 시간 복잡도를 구할 때 사용하는 중요한 공식이다.

이 점화식의 시간복잡도를 구하는 공식을 통해서 앞으로 우리는 점화식을 만들기만 하여도, 알고리즘의 시간복잡도를 알 수 있게 된다.

증명:

우선 n을 b의 거듭제곱수라고 하고, 한 문제를 푸는 데 걸리는 시간이 $O(n^d)$ 시간이 걸린다고 하자. (어차피 거듭제곱이 아니어도 같은 결과가 나오기 때문에 n을 b의 거듭제곱으로 한다.) 그리고 이 점화식을 트리의 형태로 나타내면 다음과 같은 모습이 된다.

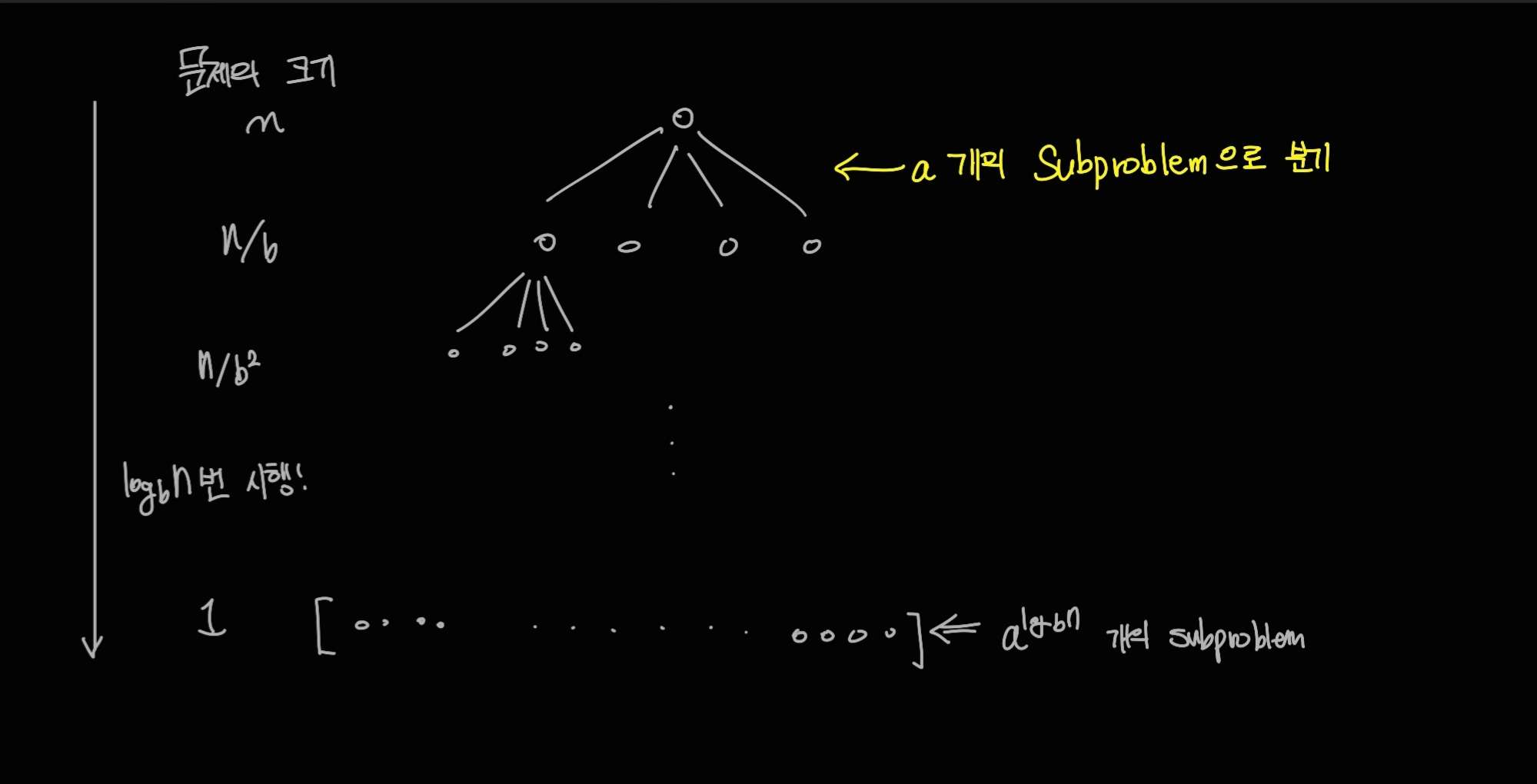
이 트리를 보면, 내려가면 내려갈수록 각각의 문제(노드)의 크기는 $\frac{1}{b}$배로 감소하고, 개수는 $a$개로 늘어나는 것을 볼 수 있다. 이렇게 되면, k번 쪼갠 후의 연산은 다음과 같은 시간 복잡도를 가지게 될 것이다:

이 식을 모든 과정 (root: 0 에서 leaf: $log_bn$ 까지) 다 더하게 되면 그 식이 $T(n)$의 시간복잡도가 되게 된다.

보면 알겠지만 등비수열이다.
결국 $\frac{a}{b^d}$에 의해 결과가 달라짐을 알 수 있다.
1보다 작은 경우: 제일 첫번째 값이 결과이므로 $O(n^d)$
1인 경우: $O(n^d) \times log_bn$ 이므로 $O(n^dlogn)$
1보다 큰 경우: 가장 마지막 값이 결과가 되므로 $O(n^{log_ba})$가 된다.

솔직히 마지막에 왜 이렇게 결론이 나오는 지는 이해하지 못하였다

예시:곱셈

두 정수의 곱셈을 예로 들어보자. 이번에도 편의를 위해 $a, b$는 모두 $2^n$ 자릿수를 가진 이진수라고 하겠다. $a \times b$ 를 수행해보자. $a, b$를 각각 $a_1, a_2, b_1, b_2$ 로 나누고, $a_1, a_2$는 $a$의 앞에서 절반의 수, 나머지 수라고 하자. 그럼

가 되는데, 이 식을 보면 분할 정복임을 알 수 있다.

이고, master theorem을 이용하면 이건 그냥 $O(n^{log_24})$가 되어서 $O(n^2)$임을 알 수 있다. 이러면 그냥 곱하는 것과 시간복잡도가 같다. 그런데 가우스의 트릭을 이용하면 4를 3으로 줄일 수 있다: $(a_1-a_2)(b_1-b_2) = a_1b_1 + a_2b_2 - (a_1b_2 + a_2b_1)$ 이걸 이용하면 덧셈한 것들을 곱하는 연산, $a_1b_1, a_2b_2$ 이렇게 세개만 수행하면, 구할 수 있으므로,

이 되어서 매우 효과적으로 연산을 수행할 수 있음을 알 수 있다.
사실은 더 좋은 방법도 있지만 후술하겠다

2. Merge sort

분할 정복 알고리즘의 가장 대표적인 친구이다. 이 알고리즘 자체는 매우 유명하기에, 내가 인상깊게 본 큐를 이용한 알고리즘과, 이 알고리즘이 왜 $O(nlogn)$의 시간 복잡도를 가지는지 알아보자.

1. 왜 NlogN의 시간복잡도인가?

Merge sort 는 왜 $O(NlogN)$의 시간 복잡도를 가지고 있는 걸까?
기본적으로 Merge sort는 array를 2개로 쪼개는 것을 반복하고, 나중에 merge를 하는 과정을 담고 있다. merge가 여기에서 $O(n)$의 시간이 걸리게 하는 것이고, $T(n)$을 생각해보면...

이고 여기에서 master theorem을 적용하면

임을 알 수 있다.

2. Queue를 이용한 merge sort 알고리즘

이제 실제로 알고리즘을 살펴보자. 이건 교과서의 내용을 그대로 가져오겠다.

function iterative-mergesort(a[1...n])
in: elements a1,a2,...,an to be sorted

Q = [] empty queue
for i = 1 to n:
	inject(Q, [ai])
while size(Q) > 1:
	inject(Q, merge(eject(Q), eject(Q)))
return eject(Q)



function merge(x[1...k], y[1...l])
if k == 0: return y[1...l]
if l == 0: return x[1...k]

if x[1] <= y[1]:
	return x[1] + merge(x[2...k], y[1...l])
else:
	return y[1] + merge(x[1...k], y[2...l])

분석: merge는 $k + l$ 번 반복되기 때문에 $O(n)$ 이 되는 것이 당연하다.
iterative-mergesort는 첫번째 for 문을 통해서 모든 원소를 쪼개는 과정을 하고, Q는 후입선출이 기본이기에 더 작은 배열이 더 앞에 배치되는 것이 자연스럽게 되기 때문에 merge가 정상적으로 이루어진다.

3. Fast Fourier transform(FFT)

원래는 이 내용을 하는 게 목표였는데 생각보다 양이 많아서 다음주로 미루게 되었다.

출처

이 블로그의 모든 내용은 Sanjoy Dasgupta 외 2인 이 작성한 'algorhithm'에서 가져왔다.