목표
이번주와 다음주는 알고리즘 특강이 있다. 그래서 알고리즘 특강 기간에는 모각코의 목표를 알고리즘 특강을 소화하는 것을 목표로 하려 한다.
dx dy 테크닉
화요일의 특강에 진행한 내용으로, 좌표상의 이동을 더 깔끔하게 처리하는 방법에 대해서 배운다. 첫 수업이라 그렇게 어려운 내용은 아니었다고 할 수 있다.
핵심
핵심은 간단하다. 상하좌우로 이동을 진행해야 하는 경우, 보통은 입력을 4개의 입력문으로 처리한다.
s = input()
if s == '상':
x, y = x, y+1
elif s == '하':
x, y = x, y-1
elif s == '좌':
x, y = x-1, y
else:
x, y = x+1, y이걸 보면 알겠지만, 상하좌우로 이동하는 코드의 대부분이 중복되는 내용이 된다.
또한, 상하좌우로 이동하기만 하면 되는 코드가 아니라, 또다른 처리를 해야 하는 경우, 실수가 발생할 가능성이 높다.
그래서 이걸 배열로 처리하는 것이 dy, dx 테크닉이 되시겠다.
dx, dy = [0, 0, -1, 1], [1, -1, 0, 0]
sToInt = ['상', '하', '좌', '우']
s = input()
for i in range(4):
if sToInt[i] == s:
s = i
x, y = x + dx[s], y + dy[s]코드가 더 짧고, 간단해졌다. 이렇게 짜인 코드는 이동을 하기 전과 후에 해야 하는 일이 있는 경우에도, 더 깔끔한 처리가 가능하게 된다. 이 코드는 dx, dy를 dict를 쓰게 되면, for 문을 안 쓸 수 있어서 더 깔끔하게 처리가 가능하다. 근데 그렇게 하면 야ㅑㅑㅑㅑㄱ간의 시간을 더 쓰는 거 같다.
팁들
1. 회전
dx, dy 테크닉의 경우 가장 중요한 것은 순서라고 생각한다. 예를 들어 회전을 진행해야 하는 경우, dx, dy의 순서는 다음과 같이 진행하는 것이 좋다: 상, 우, 하, 좌 이유는 다음 그림을 보면 알 수 있다.
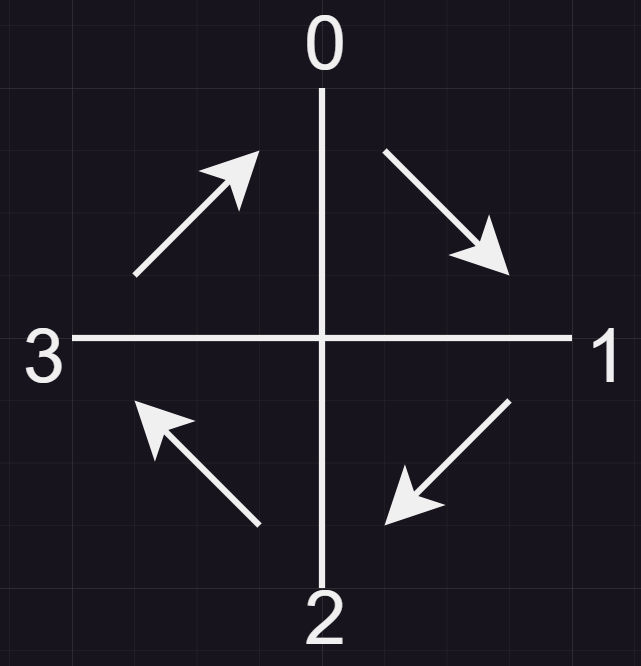
이렇게 순서를 배정하면, 다음과 같이 회전을 수행할 수 있다.
loc = 0 # 방향 가르키는 변수
# 시계 방향
loc = (loc + 1) % 4
# 반시계 방향
loc = (loc + 4 - 1) % 4왜 반시계 방향을 할 때, 그냥 -1을 해버리지 않고, 4를 더한 뒤에 -1을 하는 것일까?
그건 음수의 mod 연산이 UB(Undefined Behavior)라 그렇다. 즉, 컴파일러마다 이를 다르게 해석할 여지가 있는 코드이기 때문이다. 그래서 양수로 확정하기 위해서 +4 연산을 수행하는 것이다.
2. 행렬
행렬에서의 상하좌우는 다음과 같다.
행렬이니까 이렇게 되고, 보통 2차원 배열에서의 이동에도 이걸 사용한다.
dr, dc = [-1, 1, 0, 0], [0, 0, 1, -1]
# 상 하 좌 우 순서임시뮬레이션
정의
실제 문제가 시키는 대로 실제로 수행해보는 것.
정의가 정의다보니 완전탐색도 꽤 많이 한다.
유형 1: 완전탐색
이 유형은 완전 탐색을 진행해서 최적의 해를 찾아내는 것이다. 수업때 진행한 문제에서는 1*3짜리 박스를 배치할 것인데, 어디에 배치해야 최적의 위치에 배치할 수 있는지를 묻는 문제였다.
이런 문제의 해결법은 그냥 처음부터 끝까지 탐색하는 수 밖에 없다...
그나마 팁을 쓰자면, 왼쪽 위와 같은 기준을 잡고, 문제를 풀어나가면 만에 풀어나갈 수 있다는 것 정도?
# 코드트리 - 최고의 33 위치
n = int(input())
field = []
for i in range(n):
field.append(list(map(int, input().split())))
def find_ones(x, y) -> int: # 왼쪽 위의 좌표를 받았을 때, 얼마나 줄 지 계산하는 함수
ret = 0
for i in range(3):
for j in range(3):
ret += field[x+i][y+j]
return ret
maxCnt = 0
loc = (0,0)
#순회
for i in range(n):
if i + 2 >= n: # 만약 row가 무시되는 경우
break
for j in range(n): # 만약 col이 무시되는 경우
if j + 2 >= n:
break
curcnt = find_ones(i, j)
if maxCnt < curcnt:
maxCnt = curcnt
loc = (i, j)
print(maxCnt)유형 2: shift 연산
shift 연산은 다음과 같다. 모두 오른쪽 혹은 왼쪽으로 이동하고, 가장 오른쪽/왼쪽에 있는 원소는 제일 처음으로 이동하는 거다. 그림으로 표현하면 다음과 같다.
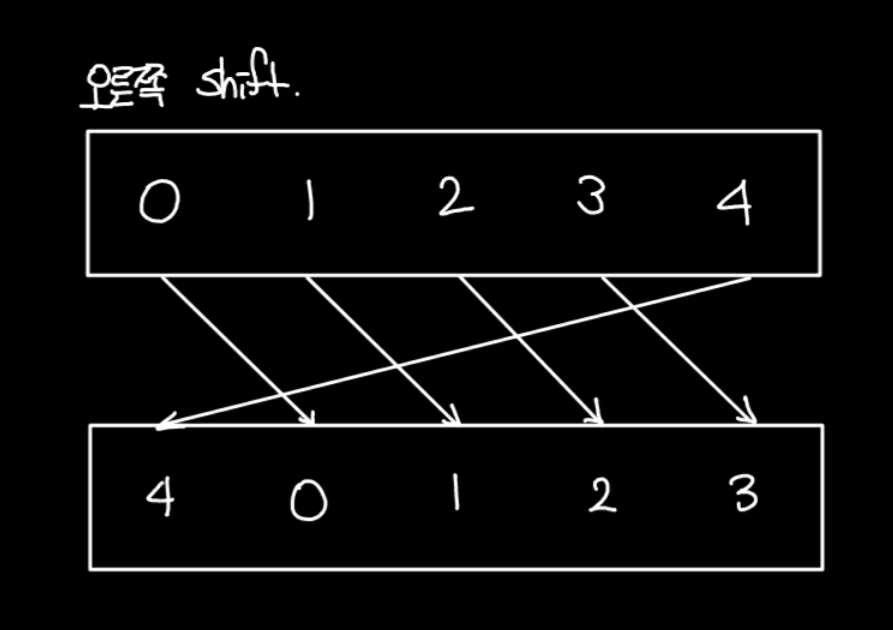
이건 그냥 제일 마지막을 저장하고, 뒤에서부터 앞으로 와가며 복붙 하면 되는 거라 아주 쉽게 할 수 있다.
유형 3: 떨어지는 거
이건 O(n * col) 로 해결이 된다. 그냥 뒤에서부터 올라가며, 비어있는 공간이 있는 경우에는 무시하고, 차 있는 경우, 채워 넣으면 되기 때문이다.
