Extended Isolation Forest
Extended Isolation Forest
- 2021 IEEE Transactions on Knowledge and Data Engineering
Isolation Forest의 수직/수평 방향의 split 방법을 보완하는 split 방법을 사용
Isolation Forest가 잘 분할하지 못하는 영역에 존재하는 anomaly도 분할하려는 목표
Introduction
전체적인 흐름은 Isolation Forest(IF)와 비슷
IF에서 tree를 만들기 위해 사용한 random split의 method를 확장
-
Isolation Forest
iTree ensemble model
axis-parallel split
↳ 축에 수직/수평 방향으로 split
random choice feature and random choice value(in feature) -
Extended Isolation Forest
IF의 split rule 변경
↳ 구분이 어려운 영역에 존재하는 anomaly를 탐지하는데 어려움이 있음
non-axis-parallel split
↳ Binary Search Tree(BST)를 생성할 때 data split을 위해 random slope가 있는 hyper-plane을 사용
Motivation
- image 출처 : Extended Isolation Forest
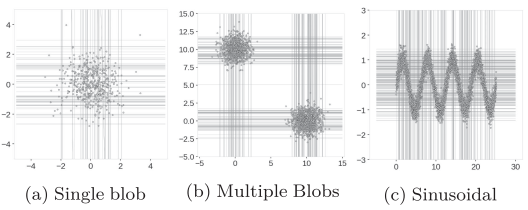
간단한 dataset에 IF를 적용한 결과 예시
좌측 : dataset
우측 : synthetic data의 anomaly score map
빨간색이 짙어질수록 높은 anomaly score를 나타냄
anomaly로 판단될 가능성이 높은 영역의 anomaly score가 정상에 가깝게 판단된 것을 확인할 수 있음 (unexpected artifacts)
정현파 data의 경우 곡선 사이의 비정상 영역까지 모두 정상으로 판단됨
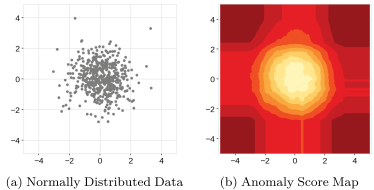
anomaly score map도 정상 데이터의 형태와 비슷하게 원의 바깥을 향할수록 anomaly score가 높아지는 것을 기대
정상 범위를 벗어나는 부분에서 직사각형 모양으로 낮은 anomaly score를 보이고 있음
이 때, 중심으로부터 같은 거리에 위치한 data point의 anomaly score가 서로 다른 값을 지닐 수 있음
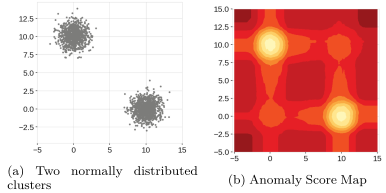
dataset의 위치는 대략 (0, 10)과 (10, 0)에 위치
score map의 해당 위치는 anomaly score가 잘 표시되어 있지만 (0, 0)과 (10, 10) 주변에도 'ghost cluster'가 생성
또한, 앞선 예제와 같이 cluster 주변 사각형 형태의 score map이 생성된 것을 확인할 수 있음
False Positive의 가능성을 높일 수 있으며 실제 데이터에 존재하지 않는 모습을 만들어낼 수 있음
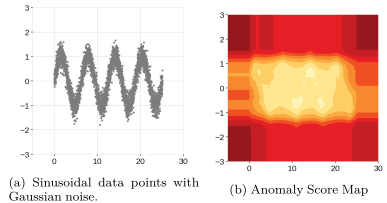
sign 곡선 사이의 data가 없는 빈 공간은 anomaly region으로 판단되어야 하는데 정상 영역이 거의 직사각형의 형태로 나타남
위의 anomaly score map과 같이 이상치가 판별되는 이유
➜ IF는 수직/수평 방향으로 split을 진행하기 때문
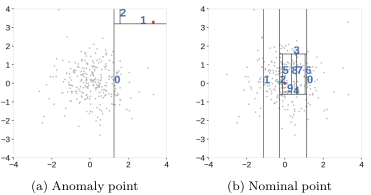
- IF의 split example
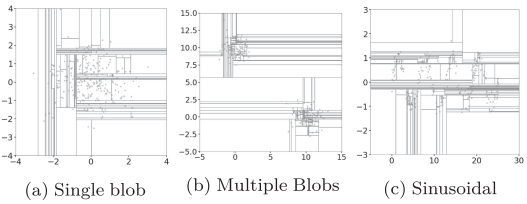
위 그림으로 봤을 때, data의 밀도가 높은 영역일수록 data point를 isolation 시키기 위해 더 많은 split이 진행되는 것을 확인할 수 있음
특히 정상 영역의 중심부에 존재하는 data point를 isolation 시키기 위해 여러 번의 split이 진행되며 data가 존재하지 않는 영역도 같이 split 됨
axis-parallel split으로 인해 data가 존재하지 않는 영역도 같이 분할되며 정상 영역으로 판단될 확률이 높아지는 것
또한 해당 부분에 존재하는 anomaly의 isolation 난이도가 높아질 것
data의 밀도가 높을 수록 더 많은 split이 필요한 것을 보여줌
split의 밀도가 낮다는 것은 해당 영역에 존재하는 point들을 isolation 시키기 쉽다는 말이므로 anomaly score가 작아짐
(b)의 (10, 10) 주변은 이상 영역으로 판단되어야 하지만 (0, 10)과 (10, 0) 주변에 존재하는 data의 isolation을 위한 split의 영향을 받아 많은 split이 발생
Extended Isolation Forest
split example
이상 영역이 정상 영역으로 판단되는 문제를 해결하기 위해 제안
IF의 split을 위한 feature selection 때, 각 feature들의 중요도 혹은 설명력을 고려하며 선택하지 않음
➜ split rule에 random slope를 추가하면 split 행위에 큰 의미 변화는 없으면서 좀 더 normal과 abnormal을 잘 구분하는 선을 그을 수 있을 것
➜ non-axis-parallel split
- EIF의 split example
기울기가 있는 선으로 split 수행

data point의 밀도가 높은 영역에 존재하는 data를 isolation 시키기 위해 비정상 영역에도 많은 split이 적용되었던 IF의 문제가 어느 정도 해결된 것을 확인할 수 있음
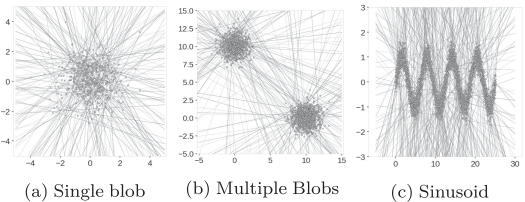
normal data의 밀도가 높은 부분을 따라 생성되는 ghost cluster와 같이 오판을 일으키는 split이 감소
data가 존재하는 영역 위주의 split
(b)의 경우 IF에서 (10, 10)과 같은 위치에서 발생했던 split 문제가 감소
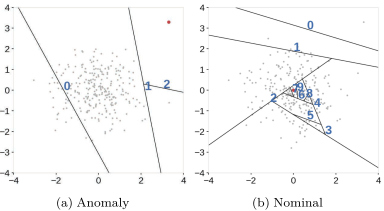
split rule
The selection of the branch cuts requires two information
-
IF : axis-parallel split
- random feature
- random value
- EIF : non-axis-parallel split
- random slope
- random intercept
split criteria
➜
dataset dimension :
dataset :
data point :
random slope :
random intercept :
selecting a random slope is the same as choosing a normal vector
➜ draw random number for each coordinate of from the standard normal distribution
selecting a random intercept
➜ draw from a uniform distribution over the range of values present at each branching point
을 만족시키는 data point
는 left branch로 아닌 경우는 right branch로 이동
data point 와 절편 사이의 직선과 normal vector 이 직교하면 내적은 0
절편 의 경우 분기점에서 사용 가능한 data로 제한되기 때문에 tree가 깊어질수록 data가 있는 곳에 누적되는 경향이 있음
branch hyperplane
dimension data의 branch cut은 최대 dimension hypterplanes를 사용
extension level에 따른 branch cut을 사용
아래 그림은 3-dimensional dat에서의 extension level에 따른 branch cut example
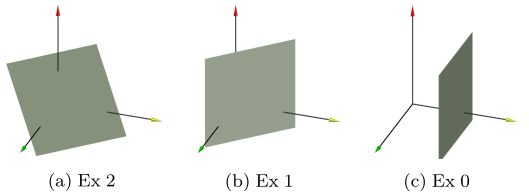
- Extension
- 모든 축과 교차하는 hyperplane을 사용하여 split
- Extension
- 해당 예시에서 hyperplane은 항상 3개의 축 중 하나의 축에 평행
- Extension
- 항상 두 개의 축과 평행한 random slice 사용
- 가장 낮은 확장 수준은 standard IF의 split과 일치
본 논문에서 제안한 extension level에 따른 split은 다차원 dataset에서 각 dimension에 따른 data의 range가 다를 때 유용할 수 있음
적절한 extension level을 선택하면 computational overhead를 감소시킬 수 있음
ex) 3-dimensional data에서 하나의 dimension에 비해 나머지 두 dimension의 범위가 훨씬 작으면 standard IF가 더 최적의 결과를 도출할 것
Algorithm
split rule을 제외한 나머지 algorithm은 standard IF와 동일
Algorithm 1 : build iForest는 IF와 같음
Algorithm 2 : build iTree

(좌) : IF
(우) : EIF
- input data 가 isolation되면 external node로 return
-
split에 사용할 normal vector 을 select
이 때 필요한 coordinate는 standard Gaussian distribuion으로부터 추출 -
intercept point 를 의 범위에서 randomly select
-
extension level에 따라 의 coordinate를 조정
-
을 만족하면 left branch로 할당
-
을 만족하면 right branch로 할당
Algorithm 3 : Path Length IF와 같음
➜ data point에 대한 average path length를 구해서 최종적으로 anomaly score를 산출
Result and Conclusion
Score Map
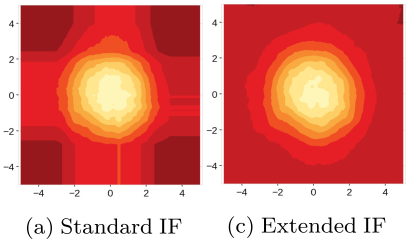
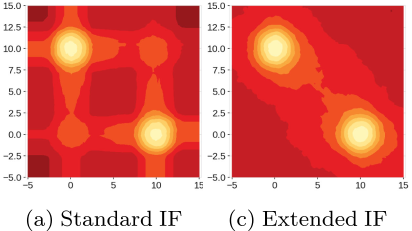
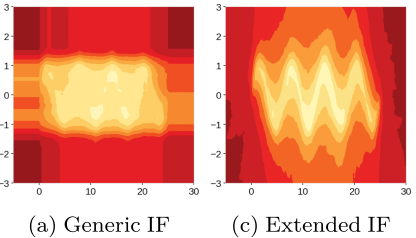
예시로 사용한 세 경우에서 발생했던 직사각형의 형태로 존재했던 artifacts가 조금 사라진 것을 확인할 수 있음
two blobs synthetic dataset의 경우 두 cluster 사이의 연결 형태가 아직 남아있음
sin graph의 경우 EIF의 score map에서 original data의 형태와 비슷하 모양으로 anomaly score가 계산된 것을 확인할 수 있음
Conclusion
-
Isolation Forest로 도출된 anomaly score map에서 잘못 판단될 가능성이 높은 영역을 포착
➜ IF의 split 방법으로 인해 생긴 이상 영역이라고 판단 -
standard Isolation Forest의 split 방법을 확장
IF : 특정 축에 평행인 선을 활용한 split
EIF : 특정 축에 평행인 선을 포함하는 random 기울기가 추가된 선을 활용한 split -
dataset에 따라 IF보다 더 더 정확한 결과를 도출할 수 있음