Robust Random Cut Forest Based Anomaly Detection On Streams
Robust Random Cut Forest Based Anomaly Detection On Streams
- 2016 Proceedings of The 33rd International Conference on Machine Learning
Binary Search Tree 기반 Algorithm으로 Stream data에 존재하는 Anomaly 탐지 목적
Isolation Forst를 real-time streaming 환경에서 적용할 수 있도록 변형
Tree 구조를 Stream data에 적용했다는 의의
본 논문의 핵심 질문
1) How do we define anomalies?
2) What data structure do we use to efficiently detect anomalies over dynamic data streams?
Differences between IF and RCF
기존의 Isolation Forest(IF) 구분되는 부분
- Feature selection
- Anomaly score
Feature Selection
-
Isolation Forest
split에 사용할 feature를 randomly select -
Extended Isolation Forest
IF와 동일 -
Random Cut Forest
feature의 범위에 따라 각 feature가 선택될 확률을 부여
Anomaly Score
- Isolation Forest
모든 Tree의 Average path length를 anomaly score로 사용
0.5를 기준으로 normal과 anomaly를 구분
-
Extended Isolation Forest
IF와 동일 -
Random Cut Forest
dataset에서 data point를 제거하고 남은 data에서 발생하는 depth 변화의 관점에서 새로운
anomaly score를 정의
model complexity 관점
Robust Random Cut Tree
robust random cut tree on point set S
: 로부터 생성된 tree
- random choice feature
번째 feature가 선택될 확률 :
➜ 각 feature의 값의 범위에 따라 해당 feature가 선택될 확률이 결정
-
randomly select value
choose ~ -
split point 보다 작으면 left branch로 크면 right branch로 분기
Anomaly Score
IF는 anomaly면 tree에서 먼저 isolation된다는 특징을 사용하여 anomaly score를 측정 ➜ average path lengh
RRCF는 model complexity 관점에서 anomaly score를 측정
➜ abnormal point increases model complexity
Displacement(DISP)
: dataset 에 존재하는 data point 를 제거했을 때, 남은 data들의 depth 변화의 총합
➜ 각 tree에서 발생하는 depth 변화의 기댓값
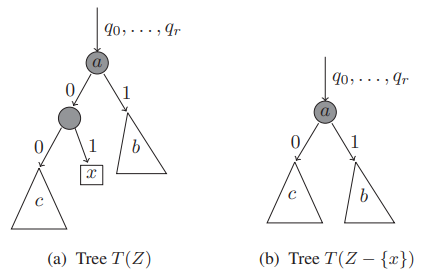
(a) : before delete
(b) : after delete
를 제거하면 sub-tree c에 존재하는 node들의 depth가 1씩 감소
와 직접적으로 연결되어 있지 않은 sub-tree b의 depth는 변화 없음
➜ 로 인한 depth 변화의 총합 == 의 sibling node에 있는 data의 개수
➜ 가 anomaly일수록 로 인한 전체 depth 변화가 클 것
Collusive Displacement(CODISP)
본 논문에서는 DISP는 masking 문제를 고려하기 위해 anomaly의 주변까지 고려하는 anomaly score를 제안
- masking : 이상치들끼리 모여 마치 정상인 것 처럼 보이게 하는 문제
masking 현상 때문에 abnormal data 옆에 가 있다면 의 는 매우 작을 것
abnormal data를 숨겨주는 colluder까지 고려하여 anomaly score를 계산
주변의 collusive cluster 를 제거했을 때 발생하는 depth의 총합을 고려
➜ but 의 size가 클수록 depth 변화가 클 것
➜ 의 size의 영향을 줄이고자 최종적으로 를 의 size로 나눈 를 사용
➜ but 의 size를 정확하게 파악할 수 없다는 문제가 존재하기 때문에 고려할 수 있는 max value를 사용
: data point
: dataset
: sub-set
Algorithm
Forget Point
- Tree 에서 에 해당하는 node 를 찾음
- node 의 parents node를 제거하고 node 의 sibling node 를 parents node로 설정 (root to 의 path ↓)
- new parents 로부터 시작하는 모든 sub-tree update
- return modified tree
Insert Point

- insert point algorithm에 대한 내용 추가
Experiments
real time data를 사용하여 실험을 진행
shingling 기법을 이용하여 preprocessing 진행
- shingling : 1-d sequence data를 n-dimensional vector로 형태를 변형하는 전처리 방법
➜ 규칙적인 변화 탐지 및 작은 noise filtering에 효과적
➜ 성능이 shingle size에 영향 받을 수 있음
synthetic data example
일정 구간에 이상치를 주입한 synthetic data를 사용하여 IF 와 RRCF를 실험
blue는 실험에 사용한 data, red는 anomaly score
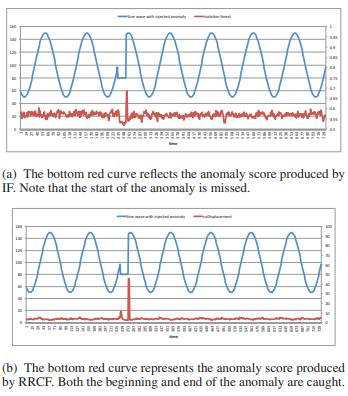
(a) IF
(b) RRCF
본 논문에서 stream data에서 이상치를 탐지할 때 start point를 탐지하는 것의 중요성을 언급
이상치의 end point 이후에 system은 이미 normal state로 돌아오기 때문에 start point를 탐지하는 것이 중요함
해당 예시에서 IF의 경우 anomaly의 start point를 탐지하지 못했지만, RRCF는 start와 end point를 탐지
tree based anomaly detection method를 time-series에 적용
multivariate time-series에 적용하기 위해서는 좀 더 고려해볼 사항이 존재
papaer github