오늘은 회귀모델을 평가하는 지표인 와 AIC에 대해 정리해 보도록 하겠습니다.
R-squared (R²)
회귀 분석에서 R-squared, 또는 R²는 분석의 핵심 지표 중 하나입니다. 이 지표는 모델이 얼마나 데이터의 변동성을 잘 설명하는지를 나타내는 값으로, '결정 계수'라고도 불립니다.
R² 값은 0과 1 사이의 값을 가지며, 1에 가까울수록 모델이 데이터를 더 잘 설명한다고 볼 수 있습니다. 수학적으로 R²는 다음과 같이 정의됩니다.
여기서 는 잔차의 제곱 합이며, 는 총 제곱 합입니다. 잔차 제곱 합은 실제 값과 모델에 의해 예측된 값 사이의 차이를 나타내고, 총 제곱 합은 실제 값과 평균 값 사이의 차이를 나타냅니다.
모델에 상수항이 포함되지 않은 경우, R²는 중심이 없는(uncentered) 방식으로 계산되어야 합니다. 이는 기존의 R²와 다른 해석을 필요로 하며, 데이터의 중심(평균)이 0이 아닌 경우에 특히 주의해야 합니다.
상수항이 없는 모델에서 R²는 종종 과대평가될 수 있으며, 이는 모델이 실제보다 더 좋은 성능을 가진 것처럼 보일 수 있음을 의미합니다. 따라서 상수항의 포함 여부는 R²의 해석에 중요한 요소가 됩니다.
AIC (Akaike Information Criterion)
Akaike Information Criterion, 약자로 AIC는 회귀 모델의 적합도를 평가하는 지표입니다. AIC는 모델의 적합도뿐만 아니라 모델의 복잡성까지 함께 고려하는 지표로, 모델이 데이터를 얼마나 잘 설명하는지와 동시에 모델이 얼마나 단순한지를 평가합니다.
AIC의 계산 공식은 다음과 같습니다.
여기서 는 모델의 파라미터 수, 은 최대 로그 우도(Maximum Log Likelihood)입니다. AIC 계산에 사용되는 '최대 로그 우도'는 모델이 관측된 데이터를 얼마나 잘 설명하는지를 수치로 나타낸 것입니다. 이 값은 데이터가 현재의 모델에서 발생할 확률을 로그로 변환하여 계산한 것으로, 이 확률이 높을수록 모델이 데이터를 잘 설명하고 있다고 볼 수 있습니다.
이 우도 값을 최대화하는 것이 목표이며, 이를 통해 최적의 모델 파라미터를 찾게 됩니다. 즉, 최대 로그 우도는 모델이 데이터와 얼마나 잘 맞는지를 나타내는 척도로, 이를 최대화하는 파라미터가 가장 적합한 모델을 의미합니다.
종합하면 AIC는 파라미터가 적고, 설명력이 좋을 수록 작은 값을 갖게 됩니다. AIC는 앞서 살펴본 R²과 달리 낮을수록 좋다고 생각할 수 있습니다. 즉, AIC 값이 낮은 모델이 데이터를 더 잘 설명하며 동시에 덜 복잡하다고 평가됩니다.
회귀 모델에서 AIC를 사용하는 이유는 모델의 복잡성과 적합도 사이의 균형을 찾기 위함입니다. 모델이 너무 단순하면 데이터의 중요한 특성을 놓칠 수 있고, 너무 복잡하면 과적합(overfitting)의 위험이 있습니다. AIC는 이 두 가지를 동시에 고려하여 모델 선택에 도움을 줍니다.
OLS 모델에서 상수항 추가의 의미
일반적인 회귀 분석에서는 모델에 상수항을 가정합니다. 상수항을 추가한다는 것은 1차 방정식의 y절편값을 추가하는 것과 같습니다. 독립 변수 X가 0일 때의 응답 변수 Y의 기대값을 제공하는 것이 상수항의 역할입니다.
상수항은 데이터가 원점에서 벗어나 있는 경우, 즉 평균이 0이 아닌 경우에 중요한 역할을 합니다. 상수항이 없는 모델은 데이터가 원점, 즉 0에서 시작한다고 가정하는 것과 같습니다. 이는 현실적인 데이터 분석에서는 비현실적인 가정이 될 수 있습니다.
상수항을 추가하는 것은 회귀선이 데이터의 중심을 통과하도록 조정하는 것을 의미합니다. 이는 모델이 데이터의 전반적인 수준을 더 잘 포착하고 해석하기 쉽게 만듭니다.
상수항 추가에 따른 지표 변화에 대한 해석
상수항을 회귀 모델에 추가했을 때 나타나는 지표 변화는 모델의 성능과 해석에 중요한 영향을 미칩니다. 특히, R²와 AIC의 변화는 모델 선택과 평가 과정에서 중요한 고려 사항이 됩니다.
R²와 AIC를 실제 예시를 통해 살펴보겠습니다. 아래는 간단한 OLS 모델입니다.
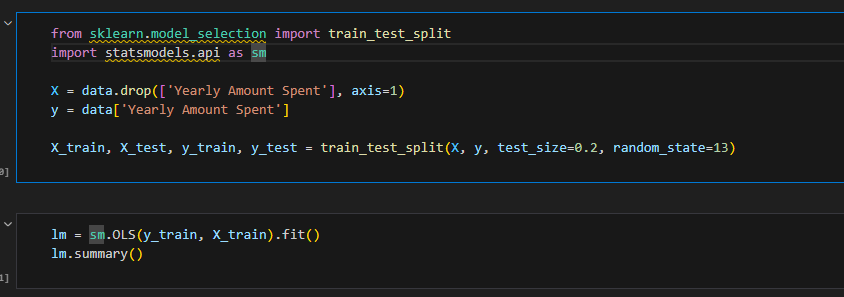
결과는 다음과 같습니다.
| Dep. Variable: | Yearly Amount Spent | R-squared (uncentered): | 0.998 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared (uncentered): | 0.998 |
| Method: | Least Squares | F-statistic: | 4.884e+04 |
| Date: | Tue, 19 Dec 2023 | Prob (F-statistic): | 0.00 |
| Time: | 20:32:07 | Log-Likelihood: | -1816.5 |
| No. Observations: | 400 | AIC: | 3641. |
| Df Residuals: | 396 | BIC: | 3657. |
| Df Model: | 4 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Avg. Session Length | 12.0166 | 0.832 | 14.440 | 0.000 | 10.381 | 13.653 |
| Time on App | 35.2145 | 1.129 | 31.197 | 0.000 | 32.995 | 37.434 |
| Time on Website | -14.4797 | 0.774 | -18.715 | 0.000 | -16.001 | -12.959 |
| Length of Membership | 60.7148 | 1.151 | 52.742 | 0.000 | 58.452 | 62.978 |
| Omnibus: | 0.449 | Durbin-Watson: | 2.036 |
|---|---|---|---|
| Prob(Omnibus): | 0.799 | Jarque-Bera (JB): | 0.571 |
| Skew: | -0.038 | Prob(JB): | 0.752 |
| Kurtosis: | 2.832 | Cond. No. | 54.7 |
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
R²가 0.998로 매우 높습니다. AIC는 3641입니다. 그런데 'Notes'란을 보면 상수항이 없다고 적혀 있습니다.
상수항을 추가하고 다시 결과를 살펴보겠습니다. statsmodels.OLS 에선 간단하게 상수항을 추가할 수 있습니다.
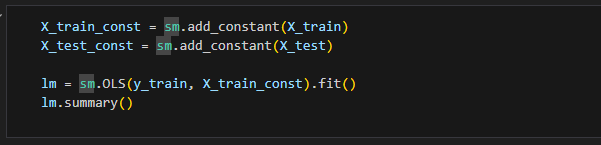
상수항을 추가한 결과는 아래와 같습니다.
| Dep. Variable: | Yearly Amount Spent | R-squared: | 0.985 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.984 |
| Method: | Least Squares | F-statistic: | 6317. |
| Date: | Tue, 19 Dec 2023 | Prob (F-statistic): | 0.00 |
| Time: | 20:40:11 | Log-Likelihood: | -1486.8 |
| No. Observations: | 400 | AIC: | 2984. |
| Df Residuals: | 395 | BIC: | 3004. |
| Df Model: | 4 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | -1046.8629 | 25.703 | -40.729 | 0.000 | -1097.395 | -996.331 |
| Avg. Session Length | 25.5891 | 0.495 | 51.742 | 0.000 | 24.617 | 26.561 |
| Time on App | 38.6640 | 0.503 | 76.893 | 0.000 | 37.675 | 39.653 |
| Time on Website | 0.4313 | 0.499 | 0.864 | 0.388 | -0.551 | 1.413 |
| Length of Membership | 61.8228 | 0.506 | 122.130 | 0.000 | 60.828 | 62.818 |
| Omnibus: | 0.857 | Durbin-Watson: | 2.089 |
|---|---|---|---|
| Prob(Omnibus): | 0.652 | Jarque-Bera (JB): | 0.637 |
| Skew: | -0.022 | Prob(JB): | 0.727 |
| Kurtosis: | 3.191 | Cond. No. | 2.63e+03 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.63e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
R²는 0.985로 조금 떨어지긴 했지만 여전히 매우 높은 수준을 보입니다. AIC는 2984로 꽤 많이 감소했습니다.
R²의 변화
상수항을 추가하면 R²는 일반적으로 감소합니다. 이는 모델이 데이터의 변동성을 설명하는 데 있어서 약간의 효율성을 잃었다는 것을 의미할 수 있습니다. 하지만, 이 감소가 반드시 모델의 성능 저하를 의미하는 것은 아닙니다. 상수항을 추가함으로써 모델이 더 현실적인 예측을 제공하고 데이터의 전반적인 패턴을 더 잘 포착할 수 있기 때문입니다.
AIC의 감소
반면, 상수항을 추가하면 AIC는 종종 크게 감소합니다. AIC의 감소는 모델의 적합도가 향상되었음을 나타내며, 추가된 상수항이 모델의 예측 능력을 상당히 향상시켰다는 것을 의미합니다. 즉, 상수항을 포함한 모델이 데이터를 더 잘 설명하고 있으며, 이는 복잡성의 증가에도 불구하고 전반적으로 더 나은 모델이라는 것을 시사합니다.
