카이제곱분포, t분포, F분포에 대해

들어가며

제로베이스 데이터스쿨에서 통계학 강의가 시작됐습니다. 오늘은 그 중에서 세 가지 카이 제곱 분포, t 분포, F 분포에 대해 정리하는 포스트를 작성해 보겠습니다.

각 분포는 정규 분포와 밀접한 관련이 있으며, 특정 상황에서 정규 분포를 대체하거나 보완하는 형태로 사용됩니다. 카이 제곱 분포는 분산의 구간 추정이나 두 변수 간의 독립성 검증에 사용되며, t 분포는 작은 샘플 크기에서의 평균 추정에 주로 사용됩니다. F 분포는 두 분산이 동일한지 비교하는 데 사용됩니다.

카이 제곱 분포 (Chi-Squared Distribution)

카이 제곱 분포는 분산 추정과 독립성 검증을 위해 사용됩니다.

정의:
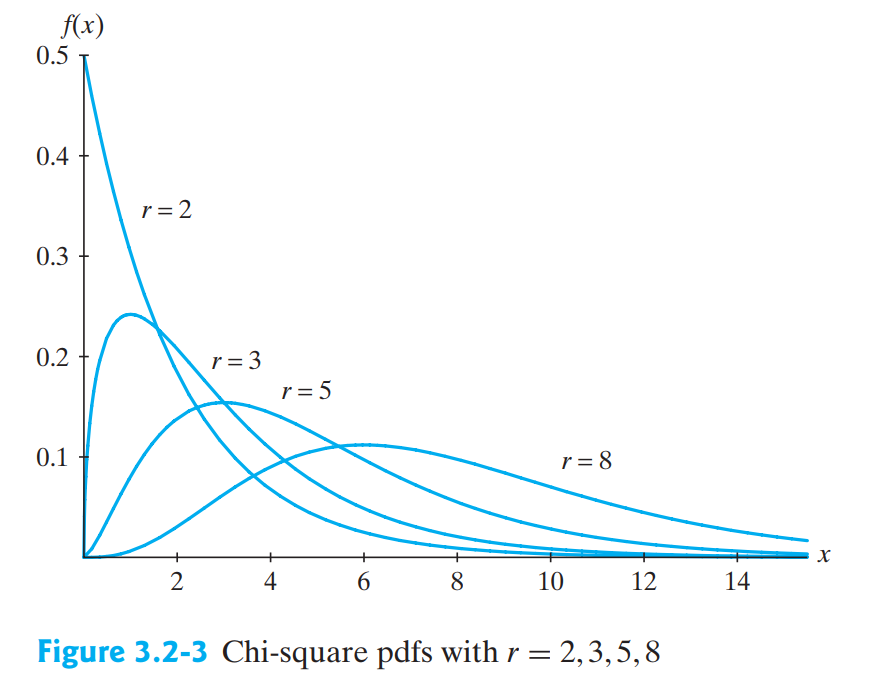
카이 제곱 분포는 독립적인 표준 정규 분포 $N(0, 1)$를 따르는 변수들의 제곱합으로 정의됩니다. 만약 $z_1, z_2, ..., z_n$이 서로 독립적인 표준 정규 분포를 따른다면, 그 제곱합 $z_1^2 + z_2^2 + ... + z_n^2$ 은 자유도 $n$을 가지는 카이 제곱 분포를 따릅니다.

기댓값과 분산:

• 자유도가 $v$인 카이 제곱 분포의 기댓값은 $v$입니다.
• 분산은 $2v$입니다.

표기법:

• 자유도 $v$인 카이 제곱 분포는 $χ^2(v)$으로 표기합니다.

카이 제곱 분포는 표준정규분포를 따른 확률변수들의 제곱의 합으로 정의되기 때문에 0 이상의 실수값만을 취합니다. 그 분포는 좌우비대칭으로 왼쪽으로 치우져 오른쪽으로 긴 꼬리를 갖는 형태입니다. 자유도가 증가함에 따라 분포는 점점 더 정규 분포와 유사한 모양으로 좌우 대칭에 가까워지게 됩니다. 이 분포는 주로 두 변수 간의 독립성을 검증하거나, 관측된 데이터가 특정 분포에 얼마나 잘 부합하는지를 평가하는 데 사용됩니다.

t 분포 (Student's t-Distribution)

t 분포는 모평균의 구간 추정에 널리 사용되며, 특히 샘플이 충분히 크지 않을 때 고려됩니다.

정의:
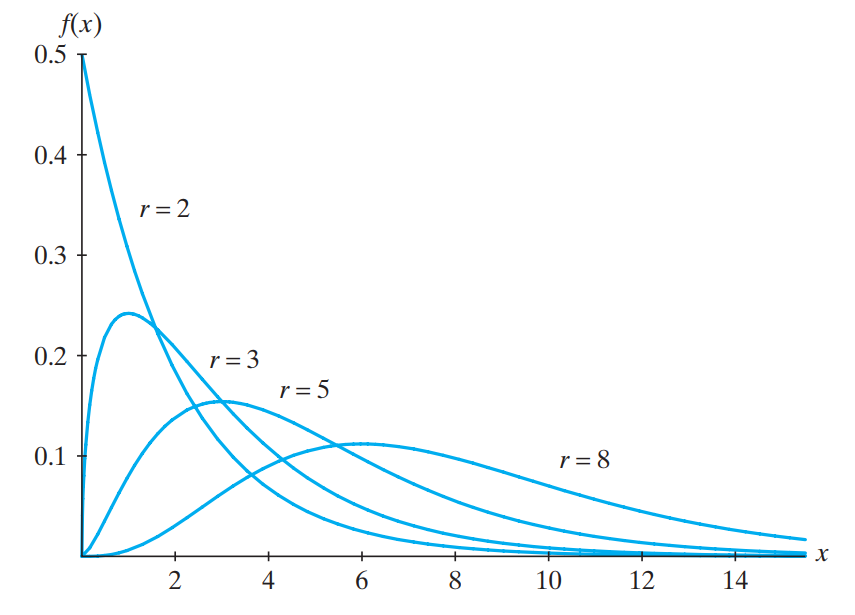
t 분포는 정규 분포의 평균을 추정할 때 사용되는 확률 분포입니다. 샘플이 충분히 크지 않아서 중심극한정리를 적용하기 어렵거나 모집단의 분산이 알려져 있지 않을 때 특히 유용합니다. 만약 $X$가 정규 분포 $N(\mu, \sigma^2)$를 따른다면, 표본 평균 $\bar{X}$와 표본 표준편차 $s$를 사용하여 계산된 $t$ 값은 자유도 $n - 1$을 가지는 t 분포를 따릅니다.
$t = \frac{\bar{X} - \mu}{s/\sqrt{n}}$

• 자유도 $n - 1$인 t 분포는 $t(n - 1)$으로 표기합니다.

t 분포는 정규 분포와 유사하지만, 꼬리 부분이 더 넓어 극단값을 더 많이 포함합니다. 이는 작은 샘플 크기에서 발생하는 추정의 불확실성을 반영한다고 볼 수 있습니다. t 분포의 형태는 자유도가 증가함에 따라 점점 더 정규 분포에 근접합니다. 모평균의 구간 추정시, 모집단의 분산을 모를 때, 특히 샘플 크기가 작을 때 t 분포를 사용합니다.

F 분포 (F-Distribution)

F 분포는 분산분석에서 사용되는 확률 분포입니다.

정의:
F 분포는 두 독립적인 카이 제곱 분포의 비율로 정의됩니다. 두 표본이 각각 자유도 $d_1$과 $d_2$를 가지는 카이 제곱 분포를 따른다고 할 때, 이 두 분포의 비율은 F 분포를 따릅니다.
$F = \frac{\chi^2(d_1)/d_1}{\chi^2(d_2)/d_2}$

• 자유도 $d_1$과 $d_2$를 가지는 F 분포는 $F(d_1, d_2)$로 표기합니다.

F 분포는 두 집단 간의 분산 차이를 비교하는 데 사용됩니다. F 분포는 비대칭적이며, 오직 양의 값만을 가집니다. 카이제곱분포가 양의 실수값만을 갖기에 카이제곱분포 분포를 따른 두 분포의 비율로 정의되는 F분포도 당연히 양의 값만을 갖습니다. F분포는 좌우비대칭으로 왼쪽으로 치우쳐 있고 으른쪽으로 긴 꼬리를 갖는 형태입니다. F 검정은 두 표본 집단이 같은 모집단에서 추출되었는지를 판단하는 데 특히 유용하며, 독립적인 집단 간의 분산 차이를 분석하는 데 사용됩니다.

---

통계나 확률에 대한 것들은 유독 기억의 지속시간이 짧은 느낌입니다. 그렇다면 자주 돌아봐서 갱신주기를 짧게 가져가는 수 밖에 없겠습니다.