G=(V,E)
- V : 정점, 1개 이상
- E : 간선, 0개 이상
- 무방향 그래프 : (V0,V1)
- 방향 그래프 : <V0,V1>
- 가중치 그래프 : 간선에 가중치를 할당한 것

- 완전 그래프 : 최대개수의 간선을 가지는 그래프
- (n = 정점의 개수)
- 무방향 그래프 간선의 개수 : n*(n-1) / 2
- 방향 그래프 간선의 개수 : n*(n-1)
- 부분그래프
- 어떤 그래프의 정점의 일부와 간선의 일부로 이루어진 그래프
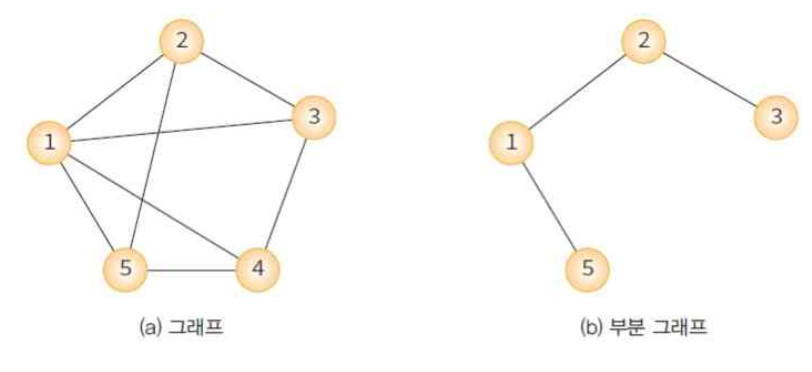
- 어떤 그래프의 정점의 일부와 간선의 일부로 이루어진 그래프
-
경로 : 정점 → 점점으로 가는 경로
- 경로의 길이 : 경로상의 간선의 수
-
단순경로 : 처음, 끝 정점을 제외하고 경로 내 정점이 서로 다름
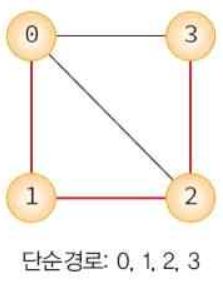
-
루프 : 출발정점 = 도착정점 and 경로
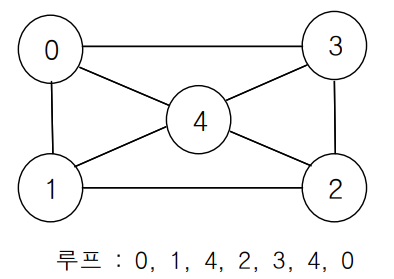
-
사이클 : 출발정점 = 도착정점 and 단순경로
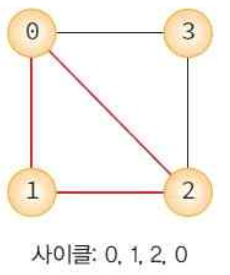
-
연결그래프 : 모든 정점쌍에 가는 경로가 존재하는 그래프
-
트리는 사이클을 가지지 않은 연결그래프이다.
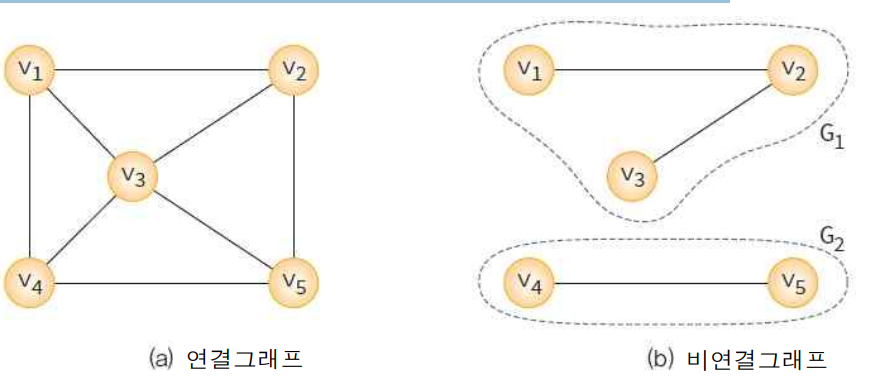
-
차수 : 정점에 부속하는 간선의 수
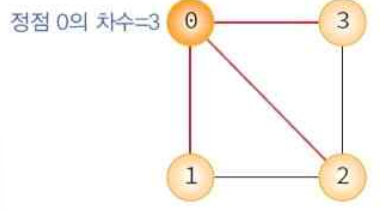
- 방향그래프 : 진입차수(O←) + 진출차수(O→) = 전체차수 - 무방향그래프 : 모든 정점의 차수 합 = 간선수 × 2 - 인접정점 : 간선에 의해 직접 연결된 정점 예) 정점 3의 인접정점 : 정점 0, 정점 2
그래프의 표현방법
인접행렬
2차원 배열 사용
- 정점수 : n, n*n의 배열 사용
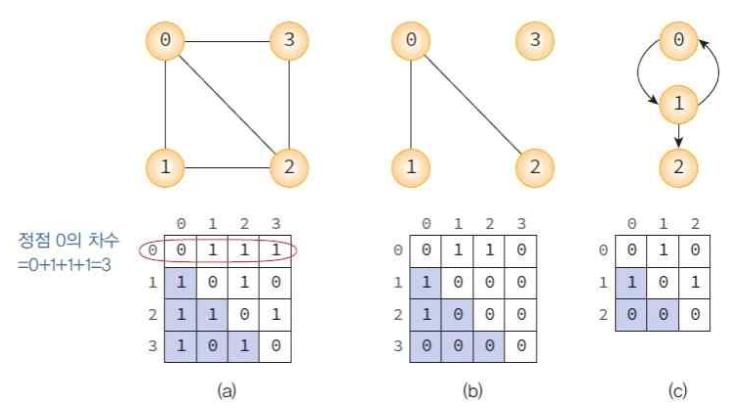
- 대각선 성분은 모두 0으로 표시됨
- 무방향 그래프(a)(b) : 대칭 행렬
→ 배열의 상위 or 하위 삼각만 저장하면 메모리 절약가능 - 방향그래프 : 대칭 or 비대칭 행렬
- 간선의 존재여부 확인 : O(1)
- 정점의 차수 확인 : O(n)
- 그래프에 존재하는 모든 간선의 수 확인 : O(n2)
인접리스트
연결리스트 사용
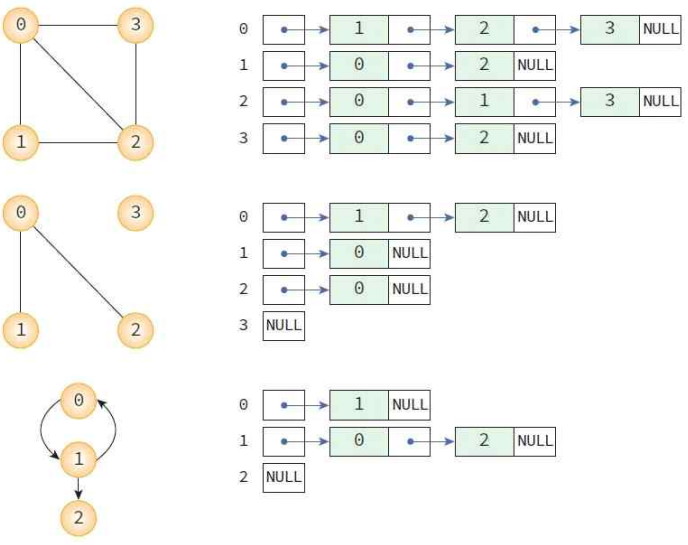
- 정점 = n개, 간선 = e개인 무방향그래프
→ n개의 연결리스트, n개의 헤더노드, 2e개의 노드 필요 - 전체 간선의 수 확인 : O(n+e)
그래프의 탐색
- 깊이우선탐색, 너비우선탐색
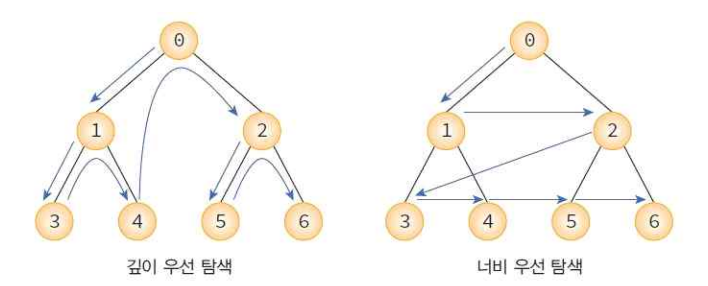
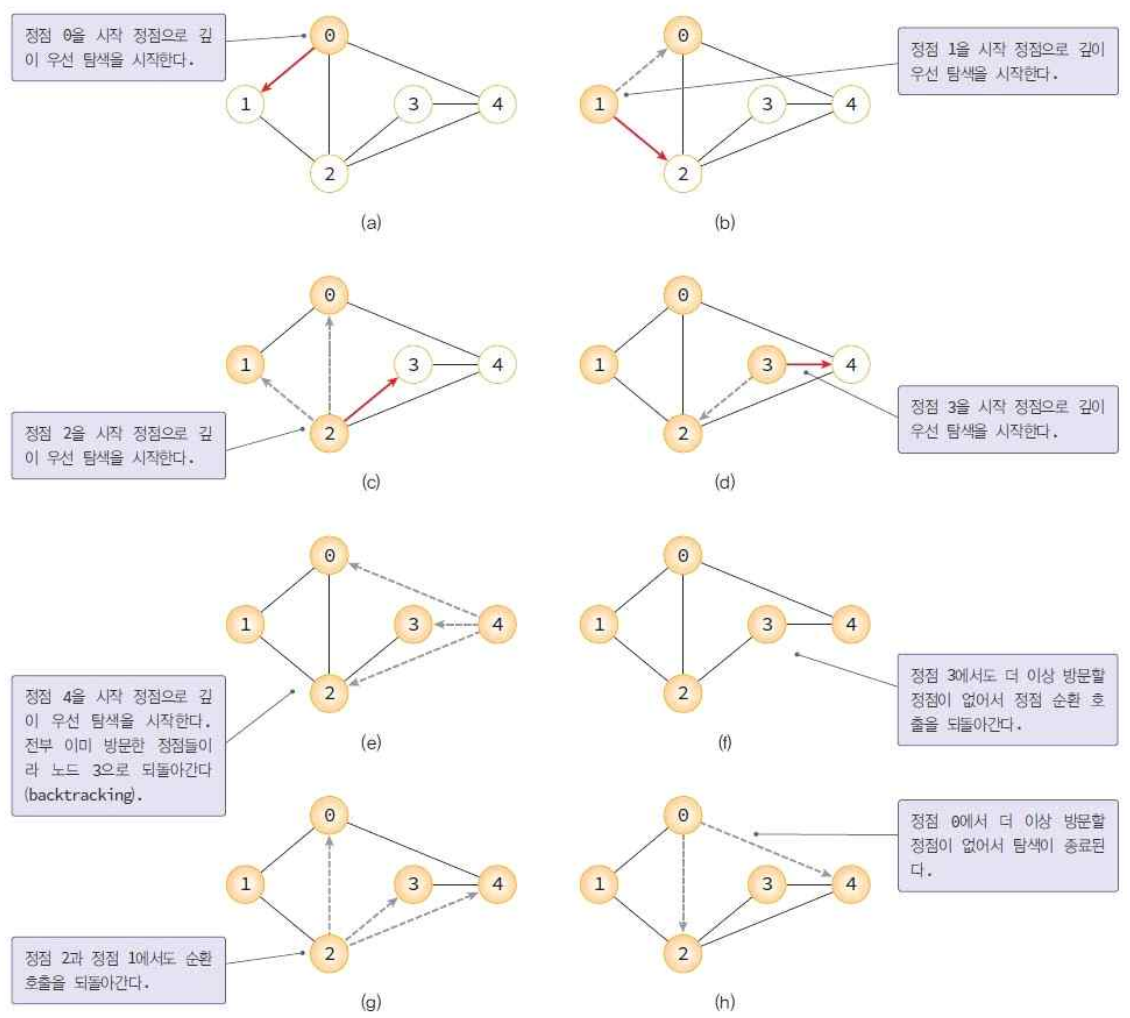
깊이우선탐색
- 장점 : 무한이 넓은 트리에 탐색하기 효과적임
- 단점 : 얻어진 해가 최단 경로가 아닐 수도 있음
- 인접리스트로 표현된 그래프 : O(n+e)
- 인접행렬로 표현된 그래프 : O(n2)
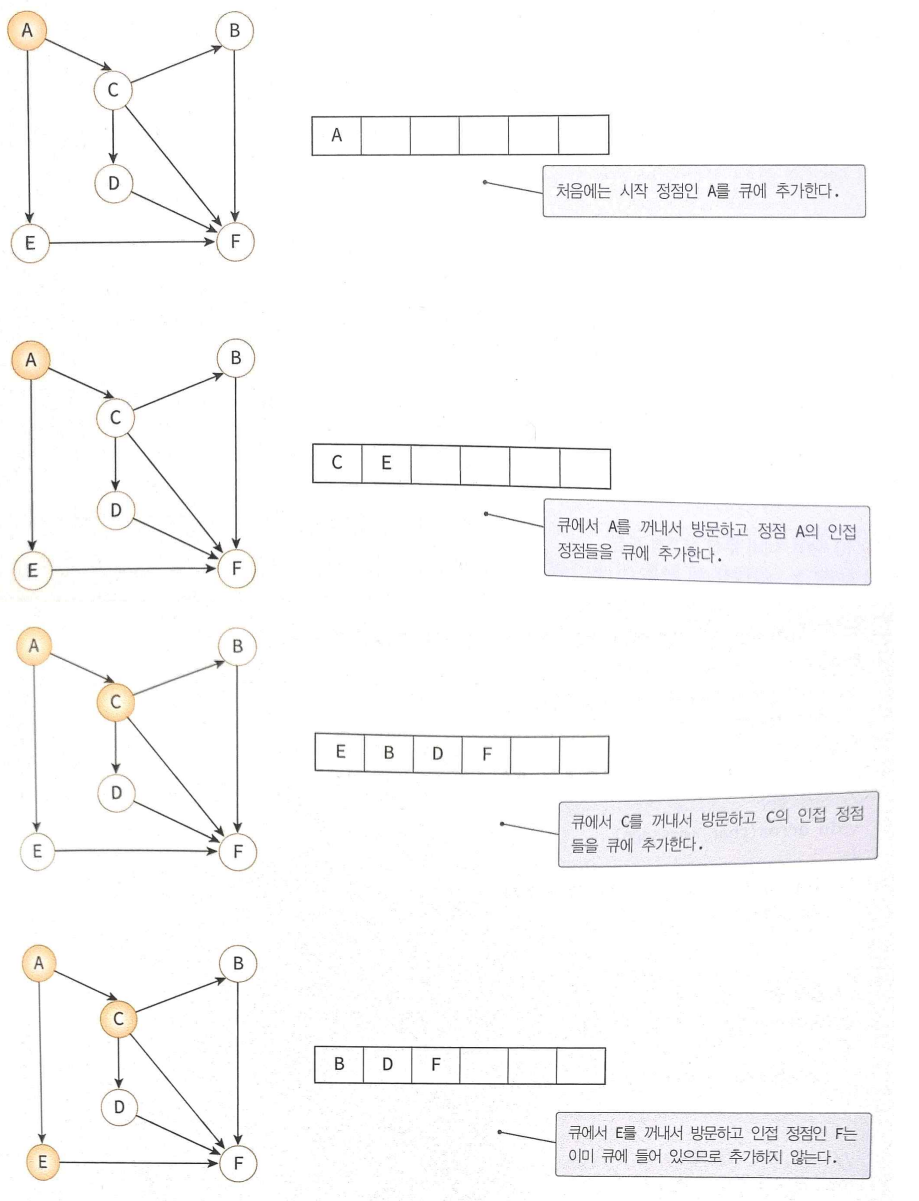
너비우선탐색
- 장점 : 깊은 트리에 효과적, 최단거리 찾기 가능
- 단점 : 낮은 레벨을 가진 트리의 노드를 찾는데 비효율적임
- 인접리스트로 표현된 그래프 : O(n+e)
- 인접행렬로 표현된 그래프 : O()
최소비용 신장 트리
- 신장트리 : 모든 정점(n개)을 포함하고, 최소 개수의 간선(n-1개)들로만 구성된 트리
Kruskal 알고리즘 : 간선 기반
- 탐욕적 방법 이용
- 선택하는 순간 가장 좋다 여겨지는 것을 선택
- 항상 최적의 해답인지 검증필요
- 시간복잡도 : O()
- 과정

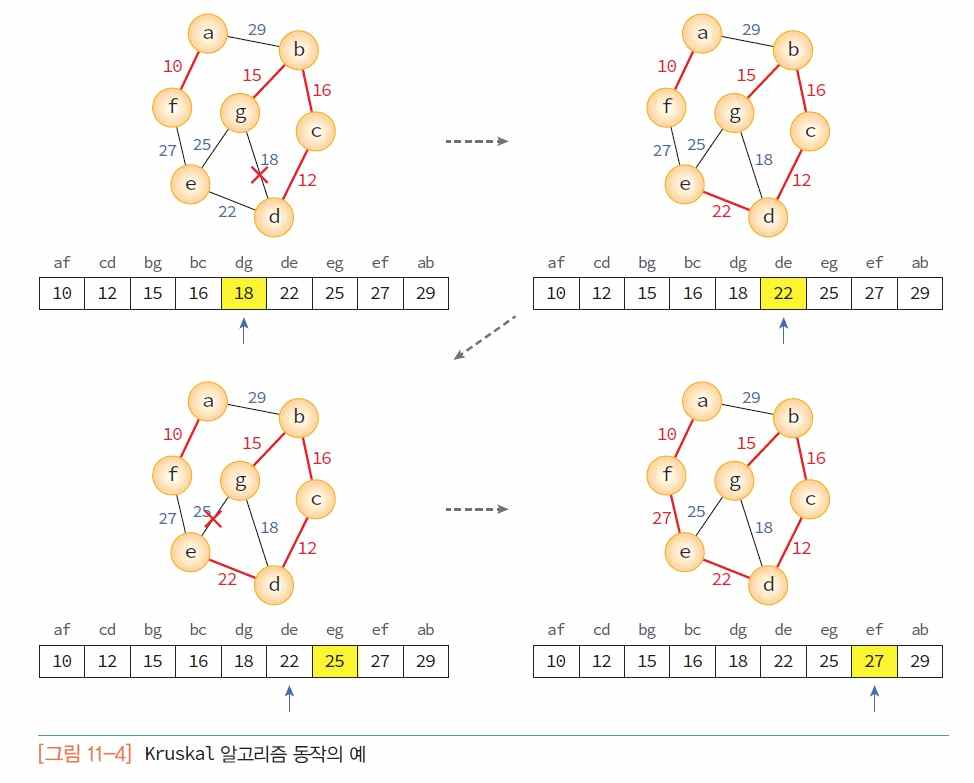
Prim 알고리즘 : 정점 기반
- 시작 정점에 관계없이 최종 그래프는 같음
- 시간복잡도O()
- 과정
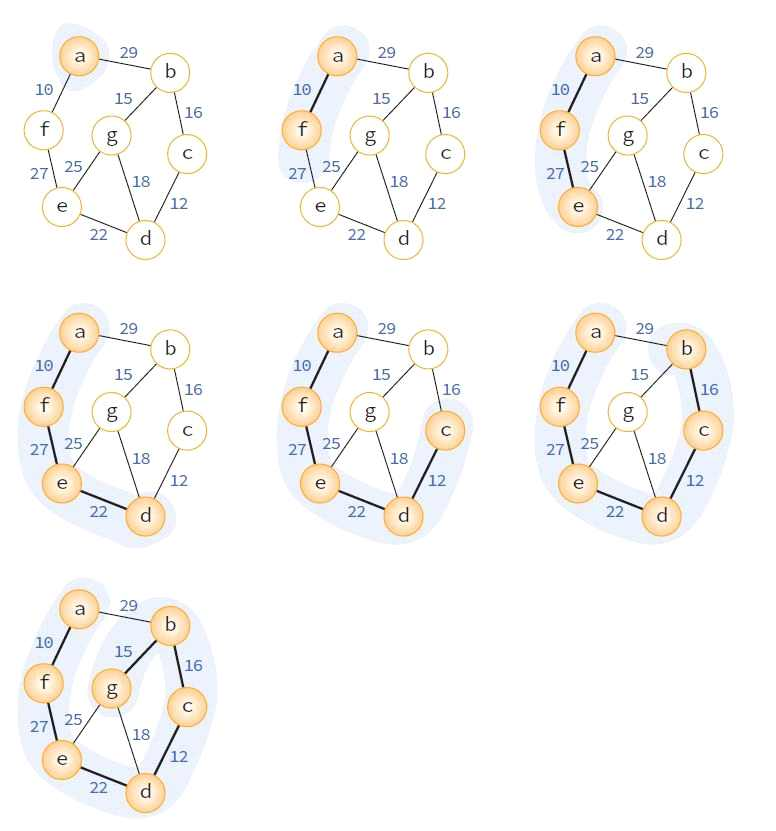
최단경로
Dijkstra 알고리즘
하나의 시작정점에서 다른 모든 정점까지의 최단경로를 구함
- 집합 S : 시작 정점으로부터 최단 경로가 이미 발견된 정점들의 집합
- distance : 시작 정점에서 집합 S에 있는 정점만을 거쳐다른 정점으로 가는 최단 거리를 기록하는 1차원 배열
- 가중치 행렬로 배열 초기화
- S = {시작정점(A), }
- distance = [시작정점에서 다른 간선까지의 가중치]
- S= {A, 시작정점에서의 최단경로에 있는 정점(B), }
- A→B 의 경로를 통해 다른 정점에 갈 수 있는 경로값이 현재 distance의 값보다 작으면 교체
- 다 할때 까지 반복
Floyd 알고리즘
하나의 시작정점에서 다른 모든 정점까지의 최단경로를 구함
- 인접행렬 : 가중치 저장, 간선이 없다면 무한대값 저장
- 가중치 행렬로 배열 A 초기화
- 정점 1을 거쳐 가는 경로와 비교해 최단경로 수정
- 정점 2를 거쳐 가는 경로와 벼교해 최단경로 수정
- ……
- 완성!