정보의 항목들이 가지로 연결될 수 있게 데이터가 조직되는 1개 이상의 노드로 구성된 유한집합
-
노드 : 트리를 구성하는 요소
-
루트노드 : 가장 높은 곳에 있는 노드
-
서브트리 : 루트노드를 제외한 나머지 노드
-
간선 : 루트와 서븥리를 연결한 선
-
부모노드 : 한 노드와 간선이 이어진 윗 노드
-
자식노드 : 한 노드와 간선이 이어진 아랫노드
-
형제노드 : 같은 레벨, 동일한 부모노드를 가지는 노드
-
조상노드 : 루트에서 그 노드까지의 경로상에 있는 모든 노드
-
후손노드 : 그 노드의 서브트리에 있는 모든 노드
-
단말 노드 : 차수가 0인 노드
-
노드의 차수 : 노드의 서브트리 수
-
트리의 차수 : 노드 차수 중 최대값
-
레벨 : 루트의 레벨 = 1, 그 외 = 부모의 레벨 + 1
-
높이(깊이) : 트리에 있는 노드의 최대 레벨 값
-
포리스트 : n≥0개의 분리된 트리들의 집합트리에서 루트를 제거한 것
이진트리
공백이거나,
루트와 왼쪽⋅오른쪽 서브트리라고 하는
2개의 분리된 이진트리로 구성된 노드의 유한집합
이진트리 순회
각 노드를 중복되지 않게 방문하는 것
- 전위순회
- VLR
- 중위순회
- LVR
- 후위순회
- LRV
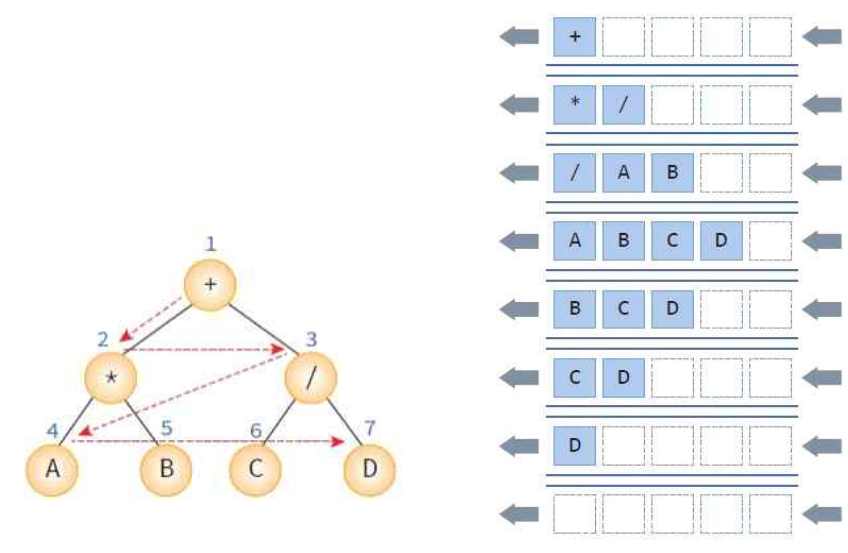
- 반복적 중위순회 - 스택 사용
- 노드수 = n일때 O(n)
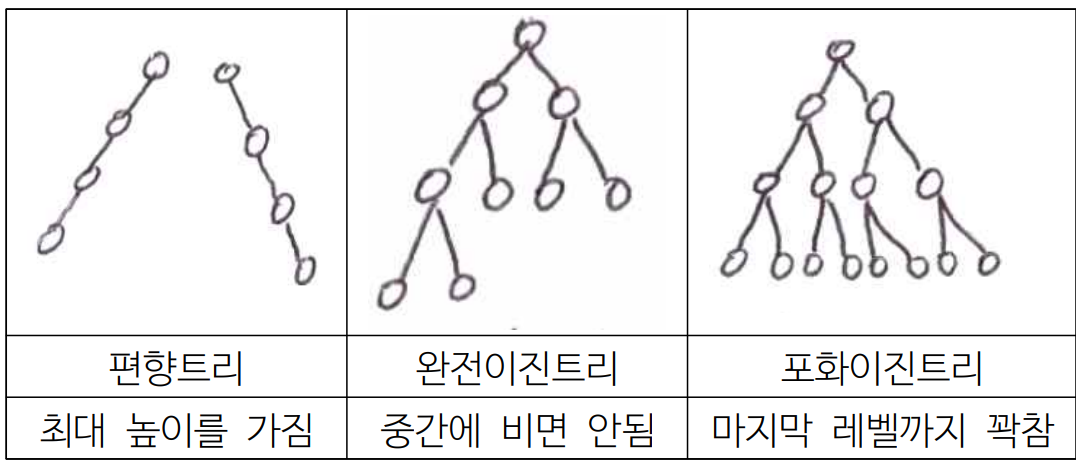
- 스택에 최대 쌓이는 개수 = 트리의 높이(완전이진트리)
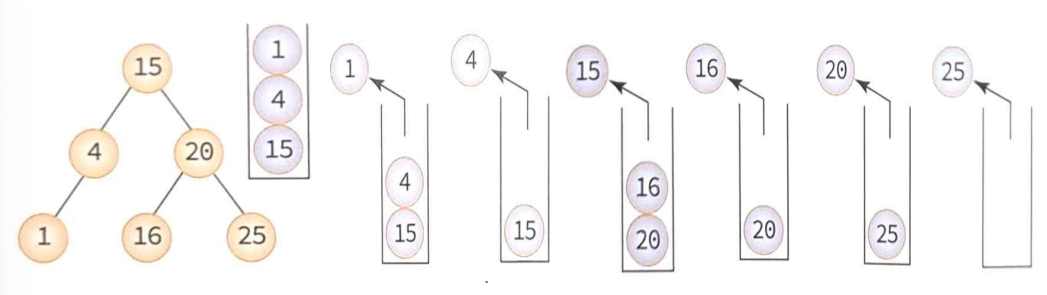
- 레벨순서 순회 - 큐 사용
- front, rear ← 0
- 공백트리면 종류
- 현재 노드 큐에 삽입
- 무한반복
- 현재 노드 큐에서 삭제
- 현재 노드가 있다면
- 현재 노드값 출력
- 만약 왼쪽자식이 있다면
- 왼쪽자식 큐에 넣기
- 만약 오른쪽 자식이 있다면
- 오른쪽자식 큐에 넣기
- 현재 노드가 없다면 끝

이진탐색트리
모든 원소가 서로 다른 키 값을 지닌 트리이며 다음과 같은 특징을 가진다.
- 한 노드에 대해 왼쪽 서브트리엔 작은값, 오른쪽 서브트리엔 큰 값이 온다.
- 중위순회시 오름차순으로 정렬 된다.
- 탐색, 삽입, 삭제 연산의 시간복잡도는 O()이다.
- 순환적 탐색
- 반복적 탐색
- 삽입
- 삭제
- 리프노드 삭제 : 해당노드만 삭제
- 자식을 1개 가진 노드 삭제
- 삭제 후 자신의 부모노드에 자식노드를 붙임
- 자식을 2개 가진 노드 삭제
- 왼쪽 서브트리에서 가장 큰 원소 or 오른쪽 서브트리에서 가장 작은 원소로 대체
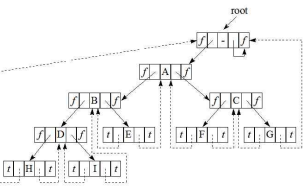
스레드 이진트리
NULL링크에 중위후속자를 저장시켜놓은 트리
- threadedPointerrk가 False면 자식, True면 중위후속자
힙
가장 큰 or 작은 값을 빠르게 찾기위해 사용
- 힙트리: 각 노드가 부모노드와 자식노드간에 일정한 순서적 성질을 가지는 완전이진트리
- 최대힙: 최대트리(각 노드 키 값이 자식 키 값과 같거나 큰 트리) & 완전이진트리
- 최소힙: 최소트리(각 노드 키 값이 자식 키 값과 같거나 작은 트리) & 완전이진트리
- 삽입(최대 힙)
- 원소 n개일 때, 힙 높이 = ⌈log2(n+1)⌉ 즉 O(log2n)
- 힙이 꽉차면 종료
- i ← 원소의 개수+1 (원소의 개수 n도 증가됨)
- i가 1이거나 삽입할노드가 부모노드보다 작을때까지
- 부모값을 자식으로 옮기기
- i ← i/2(i는 현재 노드의 인덱스)
- i에 노드 삽입
void push(int item, int *n) {
int i;
if(HEAP_FULL(*n)) exit(1); //꽉 찼으면 종료
i = ++(*n);
while( (i!=1) && (item > heap[i/2]) ) {
heap[i] = heap[i/2]; //부모값을 자식으로 옮김
i/=2;
}
heap[i] = item;
}- 삭제(최대 힙)
- 원소 n개일 때, 힙 높이 = ⌈log2(n+1)⌉ 즉 O(log2n)
- 힙이 비어있으면 종료
- item ← 루트노드(삭제할 노드)
- temp ← 마지막 노드(원소의 개수 n감소)
- parent ← 1 , child ← 2
- child가 마지막 노드를 넘을 때까지
- 자식 중 더 큰값 선택
- child값이 temp보다 작거나 같다면 반복문 탈출
- 자식값을 부모값으로 이동
- 아래 레벨로 이동 parent ← child, child ← child*2
- 부모값 ← temp
- 삭제할 노드 리턴
int pop(int *n) {
int parent, child, item, temp;
if(HEAP_EMPTY(*n)) exit(1); //비어있으면 종료
item = heap[1]; //가장 큰 값(삭제할 원소)
temp = heap[(*n)--]; //마지막 원소값 저장
parent = 1; child = 2;
while(child <= *n) {
if((child < *n) && (heap[child] < heap[child+1]))
child++; //자식 중 더 큰값 선택
if(temp >= heap[child]) break;
heap[paraent] = heap[child]; //자식값을 부모로
parent = child; //아래단계로 이동
child *= 2; //아래단계로 이동
}
heap[parent] = temp;
return item;
}