불 대수와 논리 게이트

불 대수

참,거짓(1,0)만 존재하는 숫자체계

논리합(OR)	논리곱(AND)	논리 부정(NOT)
0+0=0	0*0=0	0’=1
0+1=1	0*1=0	1’=0
1+0=1	1*0=0
1+1=1	1*1=1

불 대수 공리

공리1	A가 0이 아니면1
공리 2	0*0=0
공리 3	1*1=1
공리 4	0+0=0
공리 5	1+1=1
공리 6	10 = 01 = 0
공리 7	1+0=0+1=1

불 대수 기본정리

	OR	AND
1	A+0=A	A*0=0
2	A+A’=1	A*A’=0
3	A+A=A	A*A=A
4	A+1=1	A*1=A

기본법칙

	OR	AND
교환	A+B=B+A	AB=BA
결합	A+(B+C)=(A+B)+C	A(BC)=(AB)C
분배	A(B+C)=AB+A*C	A+(BC)=(A+B)(A+C)
드모르간	(A+B)’=A’*B’	(A*B)’=A’+B’
부정	(A’)’=A
흡수법칙	A+A*B=A	A(A+B)=A
합의의 정리	AB+BC+AC=AB+AC	(A+B)(B+C)(A+C)=(A+B)(A+C)

논리 게이트

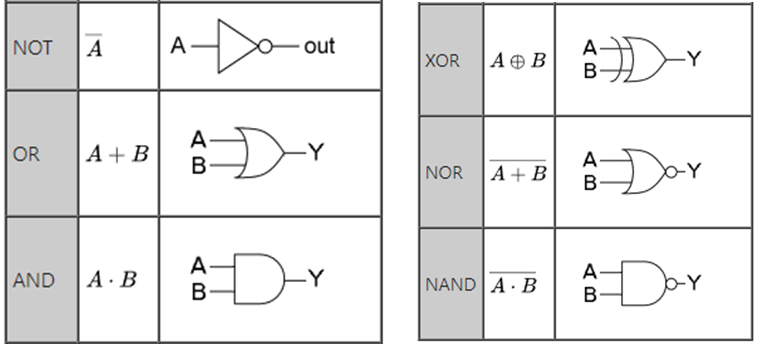
논리식의 간소화

불대수를 이용

• 복잡하다
• EX)

$A+A’B$

$= A(B+B’)+A’B$ ← (B+B’=1)

$= AB+AB’+A’B$ ← 분배법칙

$= AB+AB’+AB+A’B$ ← (AB+AB=AB)

$= A(B+B’)+B(A+A’)$ ← (A+A’=1)

$= A+B$

• 이런 식이다

카르노맵을 이용한 간소화

• 그림을 좀 그려야 하기는 하지만 불대수 보다는 간단하다
  

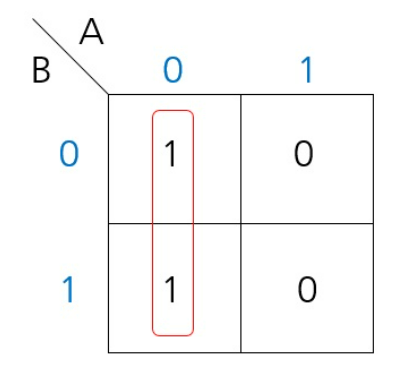
• 1을 묶을때는 묶이는 수는 최대로 묶음의 수는 최소로
• 묶음의 모양은 사각형으로
• 묶음에서 1의 개수는 2의 제곱수
• 이렇게 묶이고
  

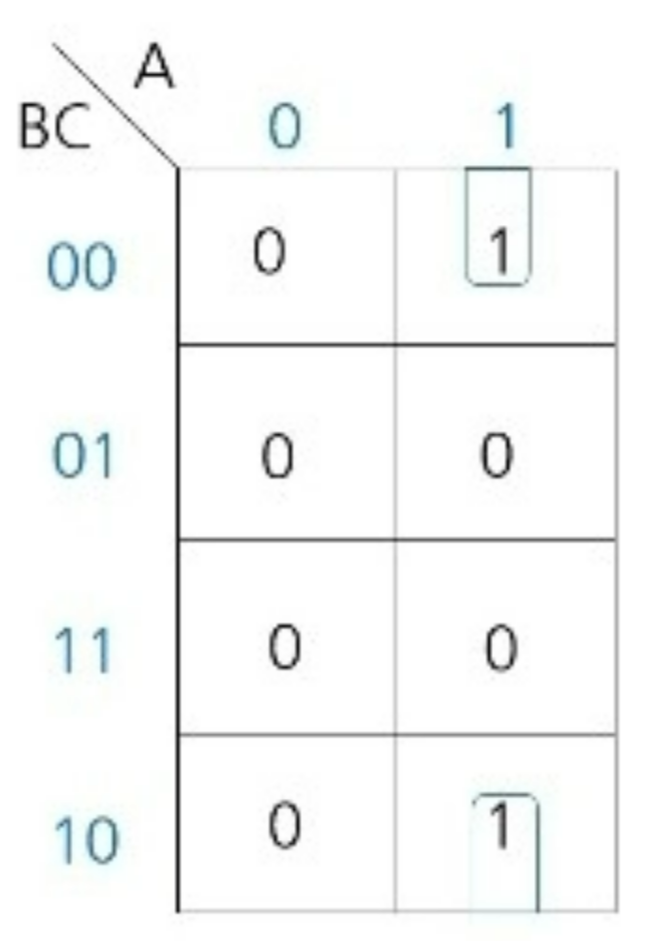
• 이렇게도 묶인다
  

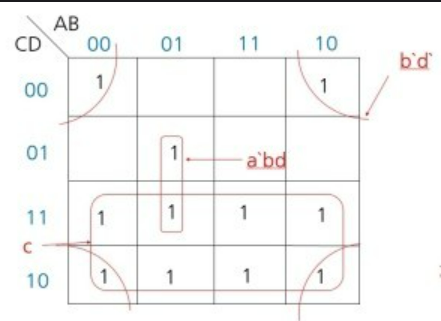
이제 묶인 1들의 공통부분 A가 1인게 공통이면 A로 A가 0인게 공통이면 A’으로

한 묶음안의 공통된 변수들은 AND로 묶음끼리는 OR로 묶는다