[ML] 머신러닝 - Dimensionality Reduction

1. 차원의 정의

공간 내 데이터의 위치를 나타내기 위해 필요한 축의 개수

2. 차원의 저주

변수가 늘어나면서 차원이 커짐에 따라 발생하는 문제

• 필요한 데이터 수의 지수 함수적 증가로 인한 정보의 밀도 감소
• 공간을 설명하기 위한 데이터의 부족
  - overfitting 문제 & 성능 감소

3. 차원 죽소

데이터를 잘 설명할 수 있는 변수의 개수 (Latent Space)는 현재 변수의 개수보다 작을 수 있다.

• 데이터를 기반으로 잠재 공간을 파악하는 것.

효과

1. 차원 저주 해결
2. 연산량 감소
3. 시각화 용이

축소 방법

1. 변수 선택 ( Feature Selection )
   - 원본 데이터의 변수 중 불필요한 변수를제거
   - 몸무게, 키, 머리 길이 -> 몸무게, 키
   
   

2. 변수 추출 ( Feature Extraction )

   • 원본 데이터의 변수들을 조합해 새로운 변수를 생성
   • 키, 몸무게, 머리 길이 -> 체구, 머리 길이
   • 체구 = 0.3몸무게 + 0.7 키

변수 추출 방법

1. PCA
   • Principal Component Analysis
2. LDA
   • Linear Discriment Analysis
3. t-SNE
   • t-distributed Stochastic Neighbor Embedding

4. PCA

여러 변수의 정보를 담고있는 주성분이라는 새로운 변수를 생성하는 차원 축소 기법
분산(Variance)을 최대로 보존하는 Hyperplane(초평면)을 찾는 과정

• 단순히 차원을 줄이는 것이 아니라,
  관측된 차원이 아닌 실제 데이터를 설명하는 차원을 찾는 것.

• 원본 데이터 셋과 투영된 Hyperplane의 평균 제곱거리를 최소화
  - 정보를 가장 적게 손실하기 때문

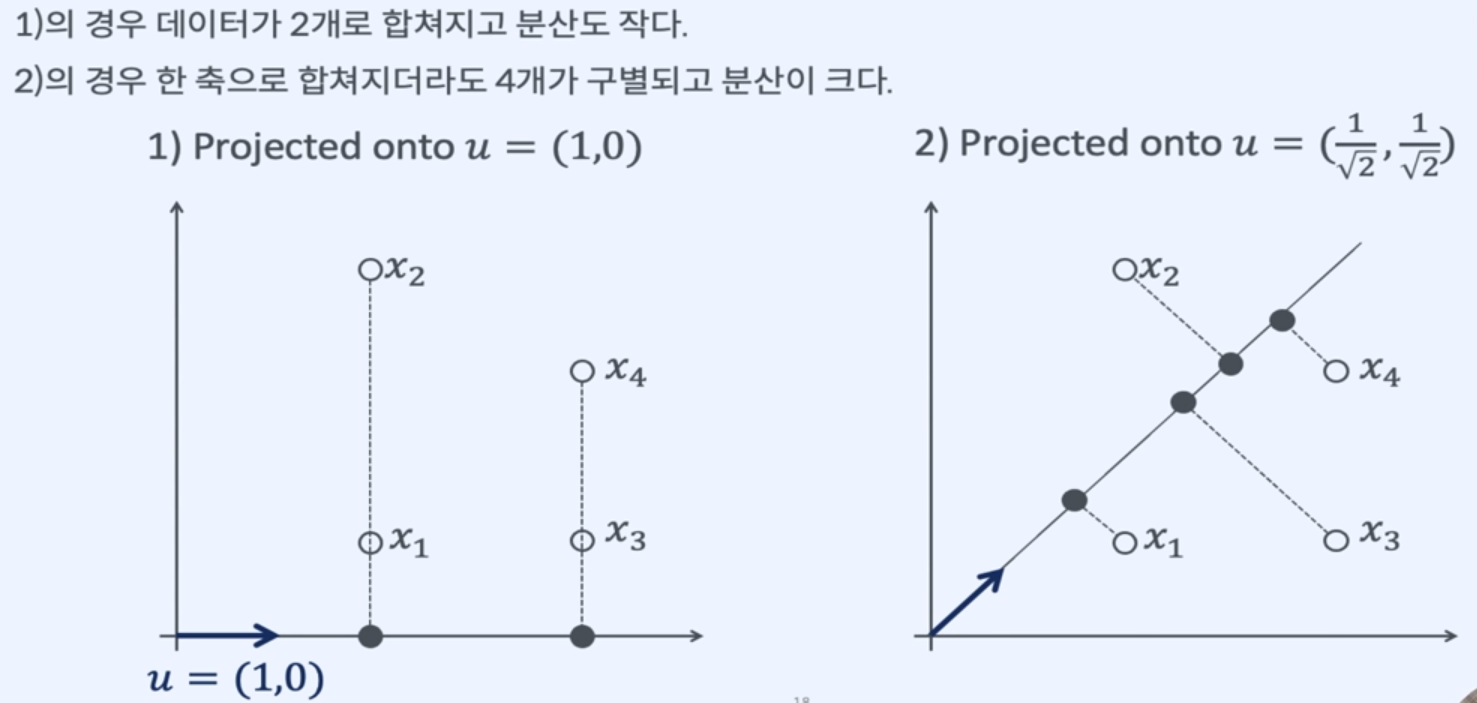
왜 분산을 최대화 하는 것이 정보의 손실을 최소화 하는 것인가?

• 차원이 줄어도 분산이 커서 각각의 데이터가 구별된다.

주성분

1. 분산을 가장 크게하는 축이 첫번째 주성분.

2. 첫번째 주성분에 직교하면서 남은 분산을 최대로 보존하는 두번째 축이 두번째 주성분

주성분 찾는 방법

1. 데이터 표준화

   • 표준화 하지 않으면 값의 크기에 따라 공분산이 영향을 받는다.

2. 표준화된 데이터의 공분산 행렬 생성

3. 고유값 분해 (Eigen Decomposition )

4. K개 벡터의 새로운 Bias

   • K를 선택하는 방법
     1. Scree Plot
     - SSE의 Elbow Point
     2. Explained Variance

5. PCA 장단점

장점

• 변수간 상관관계 및 연관성을 이용해 변수 생성
• 차원 축소로 차원 저주를 해결

단점

• 데이터에 선형성이 없다면 적용 불가능
• 데이터의 클래스를 고려하지 않기 때문에 최대 분산 방향이 특징 구분을 좋게 한다고 보장 X
• 주성분 해석을 위한 도메인 지식이 필요