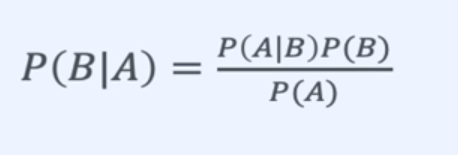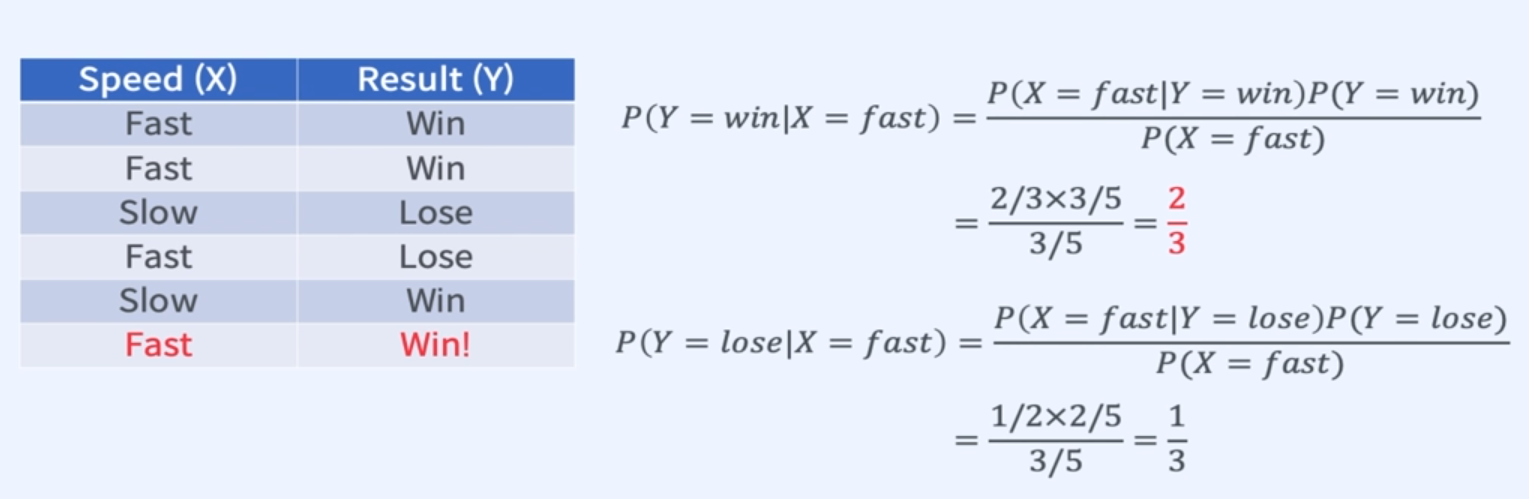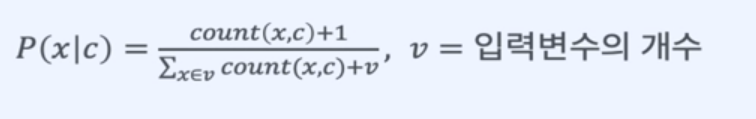1. 정의
종속 변수 Y가 주어졌을 때, 입력 변수 X들은 모두 조건부 독립.
예측 변수들의 정확한 조건부 확률은 각 조건부 확률의 곱으로 충분히 잘 추정할 수있다는 가정
- 데이터 셋을 순진하게 믿는다 -> Naive 하다
2. 수식
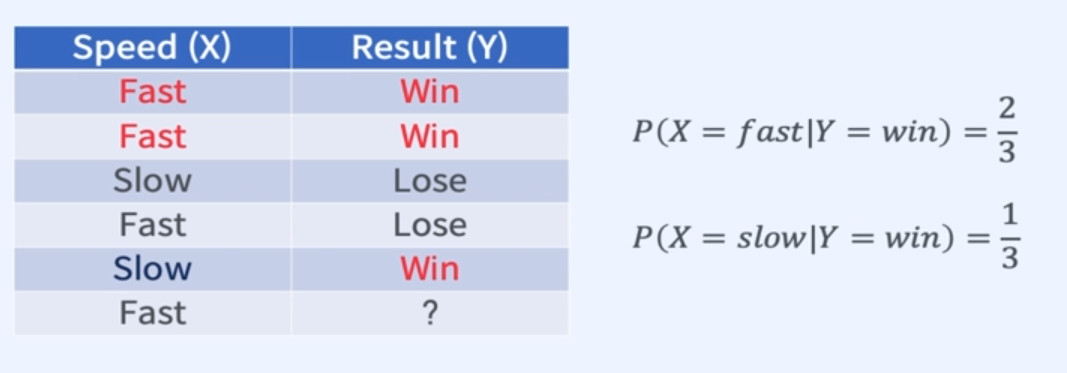
3. 결과값을 맞추는 과정
- 변수가 늘어날 수록 계산량이 많아진다.
- 계산량을 줄이기 위해 조건부 독립을 가정.

4. Laplace Smoothing
한 번도 등장하지 않는 사건이 있을 수 있다.
확률이 0이 되는 것을 방지 하기 위해
최소한의 확률을 정해준다.
5. 장단점
장점
- 변수가 많을 때 좋다
- 텍스트 데이터에서 큰 강점을 보인다.
단점
- 희귀한 확률이 등장했을 때 처리가 어렵다
- 조건부 독립이라는 가정 자체가 비현실적이다.