[ML] 기초 대수학 - 대수학적 특징

1. 속성

교환 속성

• A + B = B + A

연관 속성

• (A + B) + C = A + (B + C)

분배 속성

• A + (B + C) = (A + B) + (A + C)
• (B + C) + A = (B + C) + (C + A)

• 각 변수는 단순히 숫자가 아니라 오브젝트가 될 수 있다.
• 각 기호는 단순히 사직연산이 아니라 오브젝트 간의 연산이 될 수 있다.

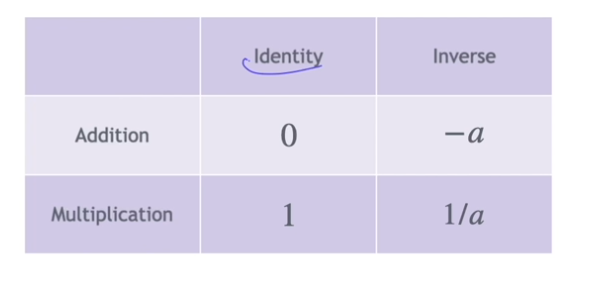
2. Identities & Inverses

1. Identities ( 항등원 )
   • 값 ( A )과 연산이 있을 때, 해당 값에 연산을 진행한 결과가
     원래의 값과 동일하게 만드는 값

     A + E = A 일 때,
     E는 연산 + ( 덧셈 ) 에 대한 항등원이다.

2. Inverses ( 역원 )

• 값 ( A )과 연산이 있을 때, 해당 값에 연산을 진행한 결과
  identity가 되게 만드는 값
  
  
• Identity를 구해야 Inverse가 정의가 된다.
  

A + E = A

• E는 덧셈에 대한 Identity

A + X = E

• A + X의 값이 Identity와 동일함으로, X는 덧셈에 대한 Inverse이다.